이번에는 Tree(트리) 구조에 대해 설명하겠습니다.
개념
트리(Tree) 구조는 계층적 데이터를 표현하고 처리하기 위해 사용됩니다.
트리는 노드(Node)들로 구성되며, 각 노드는 하나의 부모 노드와 여러 개의 자식 노드를 가질 수 있습니다.
파이썬에서는 표준 라이브러리에서 직접적인 트리 구조를 제공하지 않기 때문에 클래스와 객체를 사용하여 트리를 직접 구현해야 합니다.
주요 용어
위에서 제가 노드와 같이 알 수 없는 용어들을 언급하였는데요, 이에 대해 그림과 함께 더 자세하게 알려드리겠습니다.
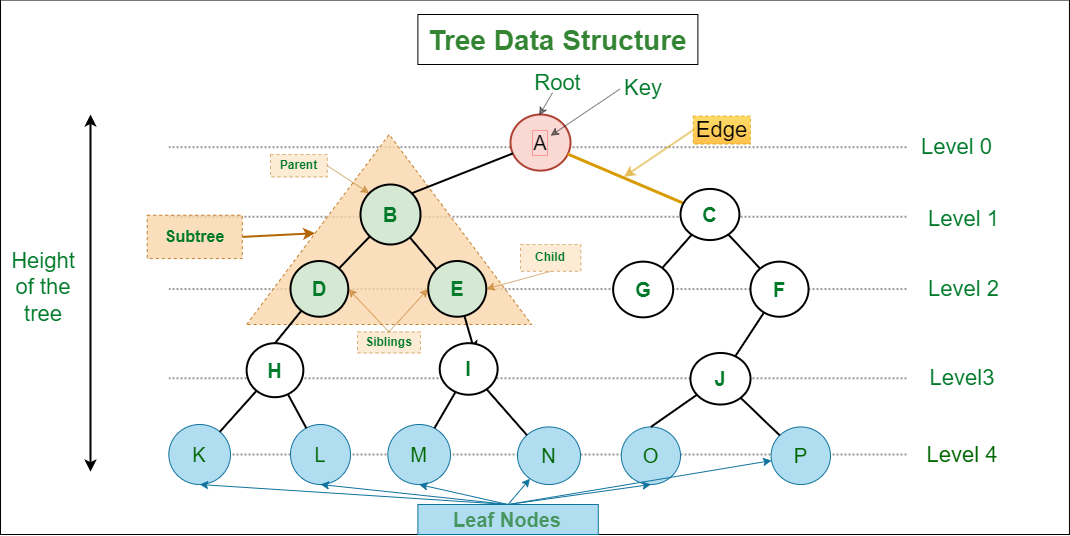
-
Root Node(루트 노드)
'A'는 트리의 최상위 노트로, 트리의 시작점이며 부모가 없는 유일한 노드입니다. 뿌리가 된다고 하여 Root Node라 불립니다. -
Edge(에지)
노드를 연결하는 선입니다. 에지는 부모-자식 노드를 연결합니다. -
Key(키)
트리의 각 노드에 할당된 값입니다. 예를 들어, 노드 'A'의 키는 'A'입니다. -
Level(레벨)
루트 노드부터 시작해서 각 노드까지의 '깊이'를 나타냅니다. 루트 노드는 레벨 0이며, 하위 레벨은 1씩 증가합니다. -
Parent Node(부모 노드)
다른 노드의 상위에 위치하는 노드입니다.
예를 들어, 'B'는 'D'와 'E'의 부모 노드입니다. -
Child Node(자식 노드)
특정 노드의 직접적인 하위 노드입니다.
'D'와 'E'는 'B'의 자식 노드입니다. -
Siblings(형제 노드)
같은 부모 노드를 공유하는 노드들입니다.
'D'와 'E'는 서로 형제입니다. -
Subtree(서브트리)
어떤 노드를 루트로 하는 그 노드와 그 자손 노드들로 구성된 트리입니다.
'B'를 루트로 하는 서브트리는 'B', 'D', 'E', 'H', 'I', 'K', 'L', 'M' 노드를 포함합니다. -
Leaf Nodes(리프 노트)
자식이 없는 노드로, 트리의 가장 아래쪽에 위치합니다.
'K', 'L', 'M', 'N', 'O', 'P' 등이 리프 노드입니다. -
Height of the tree (트리의 높이)
트리의 높이는 가장 긴 경로에 있는 노드의 레벨로 결정됩니다.
예를 들어, 루트 노드 'A'에서 리프 노드 'P'까지 가장 긴 경로의 레벨은 4이므로, 트리의 높이는 4입니다.
트리 예시
위의 개념들만 보면 대체 트리가 언제 쓰일지 감이 안오는 것은 정상입니다. 그래서 간단하게 예시를 보여드리겠습니다.
파일 시스템
파일 시스템의 구조는 트리로 표현됩니다. 각 폴더는 트리의 노드를 나타내며, 하위 폴더는 자식 노드로 표현됩니다.
파이썬으로 구현한 코드입니다.
class DirectoryNode:
def __init__(self, name):
self.name = name
self.children = []
def add_child(self, child):
self.children.append(child)
def ls(self, level=0):
print(' ' * level + self.name)
for child in self.children:
child.ls(level + 1)
# 예시: 파일 시스템 구조 만들기
root = DirectoryNode('root')
folder1 = DirectoryNode('folder1')
folder2 = DirectoryNode('folder2')
file1 = DirectoryNode('file1')
file2 = DirectoryNode('file2')
root.add_child(folder1)
root.add_child(file1)
folder1.add_child(folder2)
folder1.add_child(file2)
root.ls() # 파일 시스템 구조 출력예시 코드를 시각화를 하면 아래의 사진과 같겠습니다!

폴더의 구조를 트리로 모델링하는 것은 아래와 같은 이유가 있습니다.
-
계층적 구조 반영
실제 파일 시스템은 자연스럽게 계층적이며, 이를 트리 구조로 표현하는 것은 실세계의 구조를 그대로 반영할 수 있습니다. 디렉터리가 서브디렉터리와 파일을 포함할 수 있는 방식이 트리의 부모-자식 관계로 잘 표현됩니다. -
효율적인 탐색 및 검색
트리 구조는 탐색과 검색 연산을 효율적으로 수행할 수 있도록 합니다. 예를 들어, 특정 파일을 찾거나 디렉터리 내의 항목을 나열할 때, 트리 구조를 사용하면 불필요한 경로의 탐색을 줄일 수 있습니다. -
명확한 상대적 위치
트리는 각 노드의 상대적인 위치를 명확히 해줍니다. 이로 인해, 사용자나 프로그램이 파일 시스템 내에서 "어디에" 있는지를 쉽게 이해할 수 있습니다.
지금까지 기본 트리 구조에 대해 알아보았는데요,
다음 포스팅엔 트리에 대해 더욱 자세히 공부한 후 심화 개념에 대해 포스팅하도록 하겠습니다.
그럼 안뇽~
참고자료 및 출처
Introduction to Tree – Data Structure and Algorithm Tutorials

