데이터 사이언스 스쿨 에서 공부한 내용입니다.
3.4 특잇값 분해
정방행렬은 고유분해로 고윳값과 고유벡터를 찾을 수 있었다. 정방행렬이 아닌 행렬은 고유분해가 불가능하다. 하지만 대신 고유분해와 비슷한 특이분해를 할 수 있다.
특잇값과 특이벡터
N × M N \times M N × M A A A 특이분해(singular-decomposition) 또는 특잇값 분해(singular value decomposition) 라고 한다.
A = U Σ V T (3.4.1) A = U\Sigma V^T \tag{3.4.1} A = U Σ V T ( 3 . 4 . 1 ) 여기에서 U , Σ , V U, \Sigma, V U , Σ , V U ∈ R N × N U \in \mathbf{R}^{N \times N} U ∈ R N × N Σ ∈ R N × M \Sigma \in \mathbf{R}^{N \times M} Σ ∈ R N × M V ∈ R M × M V \in \mathbf{R}^{M \times M} V ∈ R M × M
위 조건을 만족하는 행렬 Σ \Sigma Σ 특잇값(singular value) , 행렬 U U U 왼쪽 특이벡터 (left singular vector), 행렬 V V V 오른쪽 특이벡터 (right singular vector)라고 부른다.
특이분해는 모든 행렬에 대해 가능하다.
특이값 분해 행렬의 크기
특잇값의 개수는 행렬의 열과 행의 개수 중 작은 값과 같다.
만약 N > M N > M N > M Σ \Sigma Σ M M M
A = [ u 1 u 2 u 3 ⋯ u M ⋯ u N ] [ σ 1 0 0 ⋯ 0 0 σ 2 0 ⋯ 0 0 0 σ 3 ⋯ 0 ⋮ ⋮ ⋮ ⋱ 0 0 0 ⋯ σ M 0 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 ] [ v 1 T v 2 T ⋮ v M T ] (3.4.5) A = \begin{bmatrix} \boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_3 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \cdots \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \\ \\ u_M \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \cdots \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \\ \\ u_N \\ \\ \\ \\ \\ \\ \end{matrix}} \end{bmatrix} \begin{bmatrix} \boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 \\ 0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\ 0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & 0 & \cdots & \boxed{\sigma_M \phantom{\dfrac{}{}} \!\!} \\ 0 & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & 0 \\ \end{bmatrix} \begin{bmatrix} \boxed{\begin{matrix} & & & v_1^T & & & \end{matrix}} \\ \boxed{\begin{matrix} & & & v_2^T & & & \end{matrix}} \\ \vdots \\ \boxed{\begin{matrix} & & & v_M^T & & & \end{matrix}} \\ \end{bmatrix} \tag{3.4.5} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 u 2 u 3 ⋯ u M ⋯ u N ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ 1 0 0 ⋮ 0 0 ⋮ 0 0 σ 2 0 ⋮ 0 0 ⋮ 0 0 0 σ 3 ⋮ 0 0 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ ⋯ ⋯ 0 0 0 σ M 0 ⋮ 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ v 1 T v 2 T ⋮ v M T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 5 ) 반대로 N < M N < M N < M Σ \Sigma Σ N N N
A = [ u 1 u 2 ⋯ u N ] [ σ 1 0 0 ⋯ 0 0 ⋯ 0 0 σ 2 0 ⋯ 0 0 ⋯ 0 0 0 σ 3 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ 0 0 0 ⋯ σ N 0 ⋯ 0 ] [ v 1 T v 2 T v 3 T ⋮ v N T ⋮ v M T ] (3.4.6) A = \begin{bmatrix} \boxed{\begin{matrix} \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \cdots \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ u_N \\ \\ \\ \\ \end{matrix}} \end{bmatrix} \begin{bmatrix} \boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & \boxed{\sigma_N \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\ \end{bmatrix} \begin{bmatrix} \boxed{\begin{matrix} \quad & \quad & \quad & v_1^T & \quad & \quad & \quad \end{matrix}} \\ \boxed{\begin{matrix} \quad & \quad & \quad & v_2^T & \quad & \quad & \quad \end{matrix}} \\ \boxed{\begin{matrix} \quad & \quad & \quad & v_3^T & \quad & \quad & \quad \end{matrix}} \\ \vdots \\ \boxed{\begin{matrix} \quad & \quad & \quad & v_N^T & \quad & \quad & \quad \end{matrix}} \\ \vdots \\ \boxed{\begin{matrix} \quad & \quad & \quad & v_M^T & \quad & \quad & \quad \end{matrix}} \\ \end{bmatrix} \tag{3.4.6} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 u 2 ⋯ u N ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ 1 0 0 ⋮ 0 0 σ 2 0 ⋮ 0 0 0 σ 3 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ 0 0 0 ⋮ σ N 0 0 0 ⋮ 0 ⋯ ⋯ ⋯ ⋯ 0 0 0 ⋮ 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ v 1 T v 2 T v 3 T ⋮ v N T ⋮ v M T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 6 ) 행렬의 크기만 표시하면 다음과 같다.
N { A ⏞ M = N { U ⏞ N Σ ⏞ M V T ⏞ M } M (3.4.7) N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} \; & & \; \\ \; & & \; \\ \; & A & \; \\ \; & & \; \\ \; & & \; \\ \end{matrix} }}^{\large M} = N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} \; & & & & \quad \\ \; & & & & \quad \\ \; & & \; U & & \quad \\ \; & & & & \quad \\ \; & & & & \quad \\ \end{matrix} }}^{\large N} \; \overbrace{ \boxed{ \begin{matrix} & & \\ & & \\ & \Sigma & \\ & & \\ & & \\ \end{matrix} }}^{\large M} \; \overbrace{ \boxed{ \begin{matrix} \; & & \; \\ \; & V^T & \; \\ \; & & \; \\ \end{matrix} }}^{\large M} \!\!\left.\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right\}M \tag{3.4.7} N ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ A M = N ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ U N Σ M V T M ⎭ ⎪ ⎬ ⎪ ⎫ M ( 3 . 4 . 7 ) N { A ⏞ M = N { U ⏞ N Σ ⏞ M V T ⏞ M } M (3.4.8) N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} \quad & & & & \quad \\ \quad & & A & & \quad \\ \quad & & & & \quad \\ \end{matrix} }}^{\large M} = N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} \begin{matrix} \, & & \; \\ \, & U \; \\ \, & & \; \\ \end{matrix} \end{matrix} }}^{\large N} \; \overbrace{ \boxed{ \begin{matrix} \quad & & & & \quad \\ \quad & & \Sigma & & \quad \\ \quad & & & & \quad \\ \end{matrix} }}^{\large M} \; \overbrace{ \boxed{ \begin{matrix} \; & & & & \quad \\ \; & & & & \quad \\ \; & & \; V^T & & \quad \\ \; & & & & \quad \\ \; & & & & \quad \\ \end{matrix} }}^{\large M} \!\!\left.\phantom{\begin{matrix} \\ \\ \\\\ \\ \end{matrix}}\right\}M \tag{3.4.8} N ⎩ ⎪ ⎨ ⎪ ⎧ A M = N ⎩ ⎪ ⎨ ⎪ ⎧ U N Σ M V T M ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ M ( 3 . 4 . 8 ) 예제
행렬 A A A
A = [ 3 − 1 1 3 1 1 ] (3.4.9) A = \begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \end{bmatrix} \tag{3.4.9} A = ⎣ ⎢ ⎡ 3 1 1 − 1 3 1 ⎦ ⎥ ⎤ ( 3 . 4 . 9 ) 는 다음처럼 특이분해할 수 있다.
A = [ − 1 6 2 5 − 1 6 − 2 6 − 1 5 − 2 30 − 1 6 0 5 30 ] [ 12 0 0 10 0 0 ] [ − 1 2 − 1 2 1 2 − 1 2 ] (3.4.10) A = \begin{bmatrix} -\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{5}} & -\frac{1}{\sqrt{6}} \\ -\frac{2}{\sqrt{6}} & -\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{30}} \\ -\frac{1}{\sqrt{6}} & 0 & \frac{5}{\sqrt{30}} \end{bmatrix} \begin{bmatrix} \sqrt{12} & 0 \\ 0 & \sqrt{10} \\ 0 & 0 \end{bmatrix} \begin{bmatrix} -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \tag{3.4.10} A = ⎣ ⎢ ⎢ ⎡ − 6 1 − 6 2 − 6 1 5 2 − 5 1 0 − 6 1 − 3 0 2 3 0 5 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎡ 1 2 0 0 0 1 0 0 ⎦ ⎥ ⎤ [ − 2 1 2 1 − 2 1 − 2 1 ] ( 3 . 4 . 1 0 ) 특잇값 분해의 축소형
특잇값 대각행렬에서 0인 부분은 사실상 아무런 의미가 없기 때문에 대각행렬의 0 원소 부분과 이에 대응하는 왼쪽(혹은 오른쪽) 특이벡터들을 없애 축소된 형태로 나타낼 수 있다.
N N N M M M u M + 1 , ⋯ , u N u_{M+1}, \cdots, u_N u M + 1 , ⋯ , u N
A = [ u 1 u 2 ⋯ u M ] [ σ 1 0 0 ⋯ 0 0 σ 2 0 ⋯ 0 0 0 σ 3 ⋯ 0 ⋮ ⋮ ⋮ ⋱ 0 0 0 ⋯ σ M ] [ v 1 T v 2 T ⋮ v M T ] (3.4.11) A = \begin{bmatrix} \boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \cdots \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \\ \\ u_M \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \end{bmatrix} \begin{bmatrix} \boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 \\ 0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\ 0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & 0 & \cdots & \boxed{\sigma_M \phantom{\dfrac{}{}} \!\!} \\ \end{bmatrix} \begin{bmatrix} \boxed{\begin{matrix} & & & v_1^T & & & \end{matrix}} \\ \boxed{\begin{matrix} & & & v_2^T & & & \end{matrix}} \\ \vdots \\ \boxed{\begin{matrix} & & & v_M^T & & & \end{matrix}} \\ \end{bmatrix} \tag{3.4.11} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 u 2 ⋯ u M ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ 1 0 0 ⋮ 0 0 σ 2 0 ⋮ 0 0 0 σ 3 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ 0 0 0 σ M ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ v 1 T v 2 T ⋮ v M T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 1 1 ) N N N M M M v N + 1 , ⋯ , v M v_{N+1}, \cdots, v_M v N + 1 , ⋯ , v M
A = [ u 1 u 2 ⋯ u N ] [ σ 1 0 0 ⋯ 0 0 σ 2 0 ⋯ 0 0 0 σ 3 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ σ N ] [ v 1 T v 2 T ⋮ v N T ] (3.4.12) A = \begin{bmatrix} \boxed{\begin{matrix} \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!& \cdots \!\!\!\!& \boxed{\begin{matrix} \\ \\ \\ u_N \\ \\ \\ \\ \end{matrix}} \end{bmatrix} \begin{bmatrix} \boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 \\ 0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\ 0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \boxed{\sigma_N \phantom{\dfrac{}{}} \!\!} \\ \end{bmatrix} \begin{bmatrix} \boxed{\begin{matrix} \quad & \quad & \quad & v_1^T & \quad & \quad & \quad \end{matrix}} \\ \boxed{\begin{matrix} \quad & \quad & \quad & v_2^T & \quad & \quad & \quad \end{matrix}} \\ \vdots \\ \boxed{\begin{matrix} \quad & \quad & \quad & v_N^T & \quad & \quad & \quad \end{matrix}} \\ \end{bmatrix} \tag{3.4.12} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 u 2 ⋯ u N ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ 1 0 0 ⋮ 0 0 σ 2 0 ⋮ 0 0 0 σ 3 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ 0 0 0 ⋮ σ N ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ v 1 T v 2 T ⋮ v N T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 1 2 ) 축소형의 경우에도 행렬의 크기만 표시하면 다음과 같다.
N { A ⏞ M = N { U ⏞ M Σ ⏞ M V T ⏞ M } M (3.4.13) N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} \; & & \; \\ \; & & \; \\ \; & A & \; \\ \; & & \; \\ \; & & \; \\ \end{matrix} }}^{\large M} = N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} & & \\ & & \\ & U & \\ & & \\ & & \\ \end{matrix} }}^{\large M} \; \overbrace{ \boxed{ \begin{matrix} \; & & \; \\ \; & \Sigma & \; \\ \; & & \; \\ \end{matrix} }}^{\large M} \; \overbrace{ \boxed{ \begin{matrix} \; & & \; \\ \; & V^T & \; \\ \; & & \; \\ \end{matrix} }}^{\large M} \!\!\left.\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right\}M \tag{3.4.13} N ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ A M = N ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ U M Σ M V T M ⎭ ⎪ ⎬ ⎪ ⎫ M ( 3 . 4 . 1 3 ) N { A ⏞ M = N { U ⏞ N Σ ⏞ N V T ⏞ M } N (3.4.14) N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} \quad & & & & \quad \\ \quad & & A & & \quad \\ \quad & & & & \quad \\ \end{matrix} }}^{\large M} = N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\! \overbrace{ \boxed{ \begin{matrix} \begin{matrix} \, & & \; \\ \, & U \; \\ \, & & \; \\ \end{matrix} \end{matrix} }}^{\large N} \; \overbrace{ \boxed{ \begin{matrix} \, & & \; \\ \, & \Sigma \; \\ \, & & \; \\ \end{matrix} }}^{\large N} \; \overbrace{ \boxed{ \begin{matrix} \quad & & & & \quad \\ \quad & & V^T & & \quad \\ \quad & & & & \quad \\ \end{matrix} }}^{\large M} \!\!\left.\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right\}N \tag{3.4.14} N ⎩ ⎪ ⎨ ⎪ ⎧ A M = N ⎩ ⎪ ⎨ ⎪ ⎧ U N Σ N V T M ⎭ ⎪ ⎬ ⎪ ⎫ N ( 3 . 4 . 1 4 ) 예제
행렬 A A A
A = [ 3 − 1 1 3 1 1 ] (3.4.15) A = \begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \end{bmatrix} \tag{3.4.15} A = ⎣ ⎢ ⎡ 3 1 1 − 1 3 1 ⎦ ⎥ ⎤ ( 3 . 4 . 1 5 ) 의 특이분해 축소형은 다음과 같다.
A = [ − 1 6 2 5 − 2 6 − 1 5 − 1 6 0 ] [ 12 0 0 10 ] [ − 1 2 − 1 2 1 2 − 1 2 ] (3.4.16) A = \begin{bmatrix} -\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{5}} \\ -\frac{2}{\sqrt{6}} & -\frac{1}{\sqrt{5}} \\ -\frac{1}{\sqrt{6}} & 0 \end{bmatrix} \begin{bmatrix} \sqrt{12} & 0 \\ 0 & \sqrt{10} \\ \end{bmatrix} \begin{bmatrix} -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \tag{3.4.16} A = ⎣ ⎢ ⎢ ⎡ − 6 1 − 6 2 − 6 1 5 2 − 5 1 0 ⎦ ⎥ ⎥ ⎤ [ 1 2 0 0 1 0 ] [ − 2 1 2 1 − 2 1 − 2 1 ] ( 3 . 4 . 1 6 ) 파이썬을 사용한 특이분해
numpy.linalg 서브패키지와 scipy.linalg 서브패키지에서는 특이분해를 할 수 있는 svd() 명령을 제공한다. 오른쪽 특이행렬은 전치행렬로 출력된다는 점에 주의하라.
from numpy. linalg import svd
A = np. array( [ [ 3 , - 1 ] , [ 1 , 3 ] , [ 1 , 1 ] ] )
U, S, VT = svd( A) Uarray([[-4.08248290e-01, 8.94427191e-01, -1.82574186e-01],
[-8.16496581e-01, -4.47213595e-01, -3.65148372e-01],
[-4.08248290e-01, -2.06937879e-16, 9.12870929e-01]])
Sarray([3.46410162, 3.16227766])
np. diag( S, 1 ) [ : , 1 : ] array([[3.46410162, 0. ],
[0. , 3.16227766],
[0. , 0. ]])
VTarray([[-0.70710678, -0.70710678],
[ 0.70710678, -0.70710678]])
U @ np. diag( S, 1 ) [ : , 1 : ] @ VTarray([[ 3., -1.],
[ 1., 3.],
[ 1., 1.]])
축소형을 구하려면 인수 full_matrices=False로 지정한다.
U2, S2, VT2 = svd( A, full_matrices= False ) U2array([[-4.08248290e-01, 8.94427191e-01],
[-8.16496581e-01, -4.47213595e-01],
[-4.08248290e-01, -2.06937879e-16]])
S2array([3.46410162, 3.16227766])
VT2array([[-0.70710678, -0.70710678],
[ 0.70710678, -0.70710678]])
U2 @ np. diag( S2) @ VT2array([[ 3., -1.],
[ 1., 3.],
[ 1., 1.]])
연습 문제 3.4.1
NumPy를 사용하여 다음 행렬을 특잇값 분해를 한다(축소형이 아닌 방법과 축소형 방법을 각각 사용한다). 또한 다시 곱해서 원래의 행렬이 나오는 것을 보여라.
B = [ 3 2 2 2 3 − 2 ] (3.4.17) B = \begin{bmatrix} 3 & 2 & 2 \\ 2 & 3 & -2 \end{bmatrix} \tag{3.4.17} B = [ 3 2 2 3 2 − 2 ] ( 3 . 4 . 1 7 ) C = [ 2 4 1 3 0 0 0 0 ] (3.4.18) C = \begin{bmatrix} 2 & 4 \\ 1 & 3 \\ 0 & 0 \\ 0 & 0 \\ \end{bmatrix} \tag{3.4.18} C = ⎣ ⎢ ⎢ ⎢ ⎡ 2 1 0 0 4 3 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 1 8 ) ✒️
import numpy as np
B = np. array( [ [ 3 , 2 , 2 ] , [ 2 , 3 , - 2 ] ] )
U1_full, S1_full, VT1_full = np. linalg. svd( B, full_matrices= True )
U1, S1, VT1 = np. linalg. svd( B, full_matrices= False )
C = np. array( [ [ 2 , 4 ] , [ 1 , 3 ] , [ 0 , 0 ] , [ 0 , 0 ] ] )
U2_full, S2_full, VT2_full = np. linalg. svd( C, full_matrices= True )
U2, S2, VT2 = np. linalg. svd( C, full_matrices= False )
print ( U1_full @ np. diag( S1_full, k= - 1 ) [ 1 : , : ] @ VT1_full, '\n' )
print ( U1 @ np. diag( S1) @ VT1, '\n' )
print ( U2_full @ np. diag( S2_full, k= 2 ) [ : , 2 : ] @ VT2_full, '\n' )
print ( U2 @ np. diag( S2) @ VT2, '\n' )
[[ 3. 2. 2.] [ 2. 3. -2.]]
[[ 3. 2. 2.] [ 2. 3. -2.]]
[[2. 4.] [1. 3.] [0. 0.] [0. 0.]]
[[2. 4.] [1. 3.] [0. 0.] [0. 0.]]
특잇값과 특이벡터의 관계
행렬 V V V
V T = V − 1 (3.4.19) V^T = V^{-1} \tag{3.4.19} V T = V − 1 ( 3 . 4 . 1 9 ) 특이분해된 등식의 양변에 V V V
A V = U Σ V T V = U Σ (3.4.20) AV = U\Sigma V^TV = U\Sigma \tag{3.4.20} A V = U Σ V T V = U Σ ( 3 . 4 . 2 0 ) A [ v 1 v 2 ⋯ v M ] = [ u 1 u 2 ⋯ u N ] [ σ 1 0 ⋯ 0 σ 2 ⋯ ⋮ ⋮ ⋱ ] (3.4.21) A \begin{bmatrix} v_1 & v_2 & \cdots & v_M \end{bmatrix} = \begin{bmatrix} u_1 & u_2 & \cdots & u_N \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & \cdots \\ 0 & \sigma_2 & \cdots \\ \vdots & \vdots & \ddots \\ \end{bmatrix} \tag{3.4.21} A [ v 1 v 2 ⋯ v M ] = [ u 1 u 2 ⋯ u N ] ⎣ ⎢ ⎢ ⎡ σ 1 0 ⋮ 0 σ 2 ⋮ ⋯ ⋯ ⋱ ⎦ ⎥ ⎥ ⎤ ( 3 . 4 . 2 1 ) 행렬 A A A M M M N N N
[ A v 1 A v 2 ⋯ A v N ] = [ σ 1 u 1 σ 2 u 2 ⋯ σ N u N ] (3.4.22) \begin{bmatrix} Av_1 & Av_2 & \cdots & Av_N \end{bmatrix} = \begin{bmatrix} \sigma_1u_1 & \sigma_2u_2 & \cdots & \sigma_Nu_N \end{bmatrix} \tag{3.4.22} [ A v 1 A v 2 ⋯ A v N ] = [ σ 1 u 1 σ 2 u 2 ⋯ σ N u N ] ( 3 . 4 . 2 2 ) 이 되고 N N N M M M
[ A v 1 A v 2 ⋯ A v M ] = [ σ 1 u 1 σ 2 u 2 ⋯ σ M u M ] (3.4.23) \begin{bmatrix} Av_1 & Av_2 & \cdots & Av_M \end{bmatrix} = \begin{bmatrix} \sigma_1u_1 & \sigma_2u_2 & \cdots & \sigma_Mu_M \end{bmatrix} \tag{3.4.23} [ A v 1 A v 2 ⋯ A v M ] = [ σ 1 u 1 σ 2 u 2 ⋯ σ M u M ] ( 3 . 4 . 2 3 ) 이 된다.
즉, i i i σ i \sigma_i σ i u i u_i u i v i v_i v i
A v i = σ i u i ( i = 1 , … , min ( M , N ) ) (3.4.24) Av_i = \sigma_i u_i \;\; (i=1, \ldots, \text{min}(M,N)) \tag{3.4.24} A v i = σ i u i ( i = 1 , … , min ( M , N ) ) ( 3 . 4 . 2 4 ) 이 관계는 고유분해와 비슷하지만 고유분해와는 달리 좌변과 우변의 벡터가 다르다.
예제
위에서 예로 들었던 행렬의 경우,
[ 3 − 1 1 3 1 1 ] [ − 1 2 − 1 2 ] = 12 [ − 1 6 − 2 6 − 1 6 ] (3.4.25) \begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{bmatrix} = \sqrt{12} \begin{bmatrix} -\frac{1}{\sqrt{6}} \\ -\frac{2}{\sqrt{6}} \\ -\frac{1}{\sqrt{6}} \end{bmatrix} \tag{3.4.25} ⎣ ⎢ ⎡ 3 1 1 − 1 3 1 ⎦ ⎥ ⎤ [ − 2 1 − 2 1 ] = 1 2 ⎣ ⎢ ⎢ ⎡ − 6 1 − 6 2 − 6 1 ⎦ ⎥ ⎥ ⎤ ( 3 . 4 . 2 5 ) [ 3 − 1 1 3 1 1 ] [ 1 2 − 1 2 ] = 10 [ 2 5 − 1 5 0 ] (3.4.26) \begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{bmatrix} = \sqrt{10} \begin{bmatrix} \frac{2}{\sqrt{5}} \\ -\frac{1}{\sqrt{5}} \\ 0 \\ \end{bmatrix} \tag{3.4.26} ⎣ ⎢ ⎡ 3 1 1 − 1 3 1 ⎦ ⎥ ⎤ [ 2 1 − 2 1 ] = 1 0 ⎣ ⎢ ⎡ 5 2 − 5 1 0 ⎦ ⎥ ⎤ ( 3 . 4 . 2 6 ) 가 성립한다.
연습 문제 3.4.2
NumPy를 사용하여 다음 행렬에 대해
A v i = σ i u i (3.4.27) Av_i = \sigma_i u_i \tag{3.4.27} A v i = σ i u i ( 3 . 4 . 2 7 ) 가 성립한다는 것을 계산으로 보여라.
B = [ 3 2 2 2 3 − 2 ] (3.4.28) B = \begin{bmatrix} 3 & 2 & 2 \\ 2 & 3 & -2 \end{bmatrix} \tag{3.4.28} B = [ 3 2 2 3 2 − 2 ] ( 3 . 4 . 2 8 ) C = [ 2 4 1 3 0 0 0 0 ] (3.4.29) C = \begin{bmatrix} 2 & 4 \\ 1 & 3 \\ 0 & 0 \\ 0 & 0 \\ \end{bmatrix} \tag{3.4.29} C = ⎣ ⎢ ⎢ ⎢ ⎡ 2 1 0 0 4 3 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 2 9 ) ✏️
import numpy as np
B = np. array( [ [ 3 , 2 , 2 ] , [ 2 , 3 , - 2 ] ] )
U1, S1, VT1 = np. linalg. svd( B, full_matrices= False )
V1 = VT1. T
C = np. array( [ [ 2 , 4 ] , [ 1 , 3 ] , [ 0 , 0 ] , [ 0 , 0 ] ] )
U2, S2, VT2 = np. linalg. svd( C, full_matrices= False )
V2 = VT2. T
print ( B @ V1[ : , 0 ] )
print ( S1[ 0 ] * U1[ : , 0 ] )
print ( B @ V1[ : , 1 ] )
print ( S1[ 1 ] * U1[ : , 1 ] )
print ( C @ V2[ : , 0 ] )
print ( S2[ 0 ] * U2[ : , 0 ] )
print ( C @ V2[ : , 1 ] )
print ( S2[ 1 ] * U2[ : , 1 ] ) [-3.53553391 -3.53553391]
[-3.53553391 -3.53553391]
[-2.12132034 2.12132034]
[-2.12132034 2.12132034]
[-4.46716435 -3.14809647 0. 0. ]
[-4.46716435 -3.14809647 0. 0. ]
[-0.21081425 0.29914646 0. 0. ]
[-0.21081425 0.29914646 0. 0. ]
특이분해와 고유분해의 관계
행렬 A A A A T A A^TA^{} A T A
A T A = ( V Σ T U T ) ( U Σ V T ) = V Λ V T (3.4.30) A^TA^{} = (V^{} \Sigma^T U^T)( U^{}\Sigma^{} V^T) = V^{} \Lambda^{} V^T \tag{3.4.30} A T A = ( V Σ T U T ) ( U Σ V T ) = V Λ V T ( 3 . 4 . 3 0 ) 가 되어 행렬 A A A A T A A^TA^{} A T A 행렬 A A A A T A A^TA^{} A T A 가 된다.
위 식에서 Λ \Lambda Λ N N N M M M
Λ = [ σ 1 2 0 ⋯ 0 0 σ 2 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ σ M 2 ] (3.4.31) \Lambda = \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_M^2 \\ \end{bmatrix} \tag{3.4.31} Λ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ σ 1 2 0 ⋮ 0 0 σ 2 2 ⋮ 0 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ σ M 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 3 1 ) 이고 N N N M M M
Λ = [ σ 1 2 0 ⋯ 0 ⋯ 0 0 σ 2 2 ⋯ 0 ⋯ 0 ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ 0 0 ⋯ σ N 2 ⋯ 0 ⋮ ⋮ ⋯ ⋮ ⋱ ⋮ 0 0 ⋯ 0 ⋯ 0 ] = diag ( σ 1 2 , σ 2 2 , ⋯ , σ N 2 , 0 , ⋯ , 0 ) (3.4.32) \Lambda = \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & \sigma_N^2 & \cdots & 0 \\ \vdots & \vdots & \cdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & \cdots & 0 \\ \end{bmatrix} = \text{diag}(\sigma_1^2, \sigma_2^2, \cdots, \sigma_N^2, 0, \cdots, 0) \tag{3.4.32} Λ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ 1 2 0 ⋮ 0 ⋮ 0 0 σ 2 2 ⋮ 0 ⋮ 0 ⋯ ⋯ ⋱ ⋯ ⋯ ⋯ 0 0 ⋮ σ N 2 ⋮ 0 ⋯ ⋯ ⋮ ⋯ ⋱ ⋯ 0 0 ⋮ 0 ⋮ 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = diag ( σ 1 2 , σ 2 2 , ⋯ , σ N 2 , 0 , ⋯ , 0 ) ( 3 . 4 . 3 2 ) 이다.
마찬가지 방법으로 행렬 A A A A A T AA^T A A T 가 된다는 것을 증명할 수 있다.
w, V = np. linalg. eig( A. T @ A) w array([12., 10.])
S ** 2 array([12., 10.])
V array([[ 0.70710678, -0.70710678],
[ 0.70710678, 0.70710678]])
VT. T array([[-0.70710678, 0.70710678],
[-0.70710678, -0.70710678]])
연습 문제 3.4.3
NumPy를 사용하여 행렬 A A A A A T AA^T A A T
A = [ 3 − 1 1 3 1 1 ] (3.4.33) A = \begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \end{bmatrix} \tag{3.4.33} A = ⎣ ⎢ ⎡ 3 1 1 − 1 3 1 ⎦ ⎥ ⎤ ( 3 . 4 . 3 3 ) ✏️
import numpy as np
a = np. array( [ [ 3 , - 1 ] , [ 1 , 3 ] , [ 1 , 1 ] ] )
u, s, vt = np. linalg. svd( a)
w, v = np. linalg. eig( a @ a. T)
print ( s ** 2 )
print ( w)
print ( u)
print ( v)
[12. 10.]
[ 0. 10. 12.]
[[-4.08248290e-01 8.94427191e-01 -1.82574186e-01]
[-8.16496581e-01 -4.47213595e-01 -3.65148372e-01]
[-4.08248290e-01 -2.06937879e-16 9.12870929e-01]]
[[ 1.82574186e-01 -8.94427191e-01 -4.08248290e-01]
[ 3.65148372e-01 4.47213595e-01 -8.16496581e-01]
[-9.12870929e-01 5.07704275e-16 -4.08248290e-01]]
✏️
1차원 근사
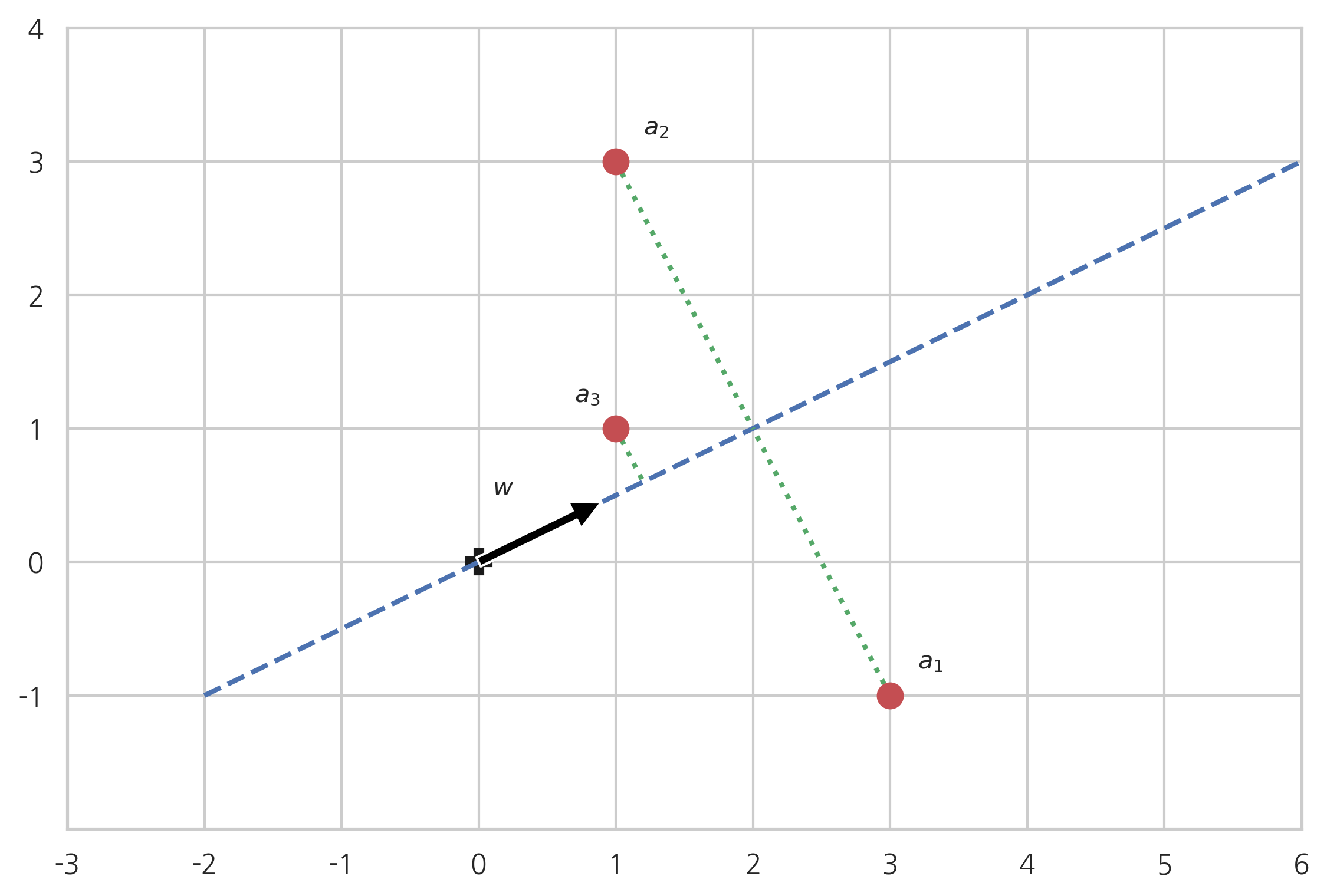
2차원 평면 위에 3개의 2차원 벡터 a 1 , a 2 , a 3 a_1, a_2, a_3 a 1 , a 2 , a 3 w w w
w = np. array( [ 2 , 1 ] ) / np. sqrt( 5 )
a1 = np. array( [ 3 , - 1 ] )
a2 = np. array( [ 1 , 3 ] )
a3 = np. array( [ 1 , 1 ] )
black = { "facecolor" : "black" }
plt. figure( figsize= ( 9 , 6 ) )
plt. plot( 0 , 0 , 'kP' , ms= 10 )
plt. annotate( '' , xy= w, xytext= ( 0 , 0 ) , arrowprops= black)
plt. plot( [ - 2 , 8 ] , [ - 1 , 4 ] , 'b--' , lw= 2 )
plt. plot( [ a1[ 0 ] , 2 ] , [ a1[ 1 ] , 1 ] , 'g:' , lw= 2 )
plt. plot( [ a2[ 0 ] , 2 ] , [ a2[ 1 ] , 1 ] , 'g:' , lw= 2 )
plt. plot( [ a3[ 0 ] , 1.2 ] , [ a3[ 1 ] , 0.6 ] , 'g:' , lw= 2 )
plt. plot( a1[ 0 ] , a1[ 1 ] , 'ro' , ms= 10 )
plt. plot( a2[ 0 ] , a2[ 1 ] , 'ro' , ms= 10 )
plt. plot( a3[ 0 ] , a3[ 1 ] , 'ro' , ms= 10 )
plt. text( 0.1 , 0.5 , "$w$" )
plt. text( a1[ 0 ] + 0.2 , a1[ 1 ] + 0.2 , "$a_1$" )
plt. text( a2[ 0 ] + 0.2 , a2[ 1 ] + 0.2 , "$a_2$" )
plt. text( a3[ 0 ] - 0.3 , a3[ 1 ] + 0.2 , "$a_3$" )
plt. xticks( np. arange( - 3 , 15 ) )
plt. yticks( np. arange( - 1 , 5 ) )
plt. xlim( - 3 , 6 )
plt. ylim( - 2 , 4 )
plt. show( )
벡터 w w w a i a_i a i
∥ a i ⊥ w ∥ 2 = ∥ a i ∥ 2 − ∥ a i ∥ w ∥ 2 = ∥ a i ∥ 2 − ( a i T w ) 2 (3.4.34) \Vert a_i^{\perp w}\Vert^2 = \Vert a_i\Vert^2 - \Vert a_i^{\Vert w}\Vert^2 = \Vert a_i\Vert^2 - (a_i^Tw)^2 \tag{3.4.34} ∥ a i ⊥ w ∥ 2 = ∥ a i ∥ 2 − ∥ a i ∥ w ∥ 2 = ∥ a i ∥ 2 − ( a i T w ) 2 ( 3 . 4 . 3 4 ) 벡터 a 1 , a 2 , a 3 a_1, a_2, a_3 a 1 , a 2 , a 3 A A A
A = [ a 1 T a 2 T a 3 T ] (3.4.35) A = \begin{bmatrix} a_1^T \\ a_2^T \\ a_3^T \end{bmatrix} \tag{3.4.35} A = ⎣ ⎢ ⎡ a 1 T a 2 T a 3 T ⎦ ⎥ ⎤ ( 3 . 4 . 3 5 ) 행벡터의 놈의 제곱의 합은 행렬의 놈이므로 모든 점들과의 거리의 제곱의 합은 행렬의 놈으로 계산된다. (연습 문제 2.3.2)
∑ i = 1 3 ∥ a i ⊥ w ∥ 2 = ∑ i = 1 3 ∥ a i ∥ 2 − ∑ i = 1 3 ( a i T w ) 2 = ∥ A ∥ 2 − ∥ A w ∥ 2 (3.4.36) \begin{aligned} \sum_{i=1}^3 \Vert a_i^{\perp w}\Vert^2 &= \sum_{i=1}^3 \Vert a_i\Vert^2 - \sum_{i=1}^3 (a_i^Tw)^2 \\ &= \Vert A \Vert^2 - \Vert Aw\Vert^2 \\ \end{aligned} \tag{3.4.36} i = 1 ∑ 3 ∥ a i ⊥ w ∥ 2 = i = 1 ∑ 3 ∥ a i ∥ 2 − i = 1 ∑ 3 ( a i T w ) 2 = ∥ A ∥ 2 − ∥ A w ∥ 2 ( 3 . 4 . 3 6 ) 점 a i a_i a i A A A ∥ A w ∥ 2 \Vert Aw\Vert^2 ∥ A w ∥ 2 w w w
arg max w ∥ A w ∥ 2 (3.4.37) \arg\max_w \Vert Aw \Vert^2 \tag{3.4.37} arg w max ∥ A w ∥ 2 ( 3 . 4 . 3 7 ) 1차원 근사의 풀이
위에서 예로 든 행렬 A ∈ R 3 × 2 A \in \mathbf{R}^{3 \times 2} A ∈ R 3 × 2
첫 번째 특잇값: σ 1 \sigma_1 σ 1 u 1 ∈ R 3 u_1 \in \mathbf{R}^{3} u 1 ∈ R 3 v 1 ∈ R 2 v_1 \in \mathbf{R}^{2} v 1 ∈ R 2
두 번째 특잇값: σ 2 \sigma_2 σ 2 u 2 ∈ R 3 u_2 \in \mathbf{R}^{3} u 2 ∈ R 3 v 2 ∈ R 2 v_2 \in \mathbf{R}^{2} v 2 ∈ R 2
첫 번째 특잇값 σ 1 \sigma_1 σ 1 σ 2 \sigma_2 σ 2
σ 1 ≥ σ 2 (3.4.38) \sigma_1 \geq \sigma_2 \tag{3.4.38} σ 1 ≥ σ 2 ( 3 . 4 . 3 8 ) 또한 위에서 알아낸 것처럼 A에 오른쪽 특이벡터를 곱하면 왼쪽 특이벡터 방향이 된다.
A v 1 = σ 1 u 1 (3.4.39) A v_1 = \sigma_1 u_1 \tag{3.4.39} A v 1 = σ 1 u 1 ( 3 . 4 . 3 9 ) A v 2 = σ 2 u 2 (3.4.40) A v_2 = \sigma_2 u_2 \tag{3.4.40} A v 2 = σ 2 u 2 ( 3 . 4 . 4 0 ) 오른쪽 특이벡터 v 1 , v 2 v_1, v_2 v 1 , v 2
우리는 ∥ A w ∥ \Vert Aw\Vert ∥ A w ∥ w w w w w w v 1 , v 2 v_1, v_2 v 1 , v 2
w = w 1 v 1 + w 2 v 2 (3.4.41) w = w_{1} v_1 + w_{2} v_2 \tag{3.4.41} w = w 1 v 1 + w 2 v 2 ( 3 . 4 . 4 1 ) 단, w w w w 1 , w 2 w_{1}, w_{2} w 1 , w 2
w 1 2 + w 2 2 = 1 (3.4.42) w_{1}^2 + w_{2}^2 = 1 \tag{3.4.42} w 1 2 + w 2 2 = 1 ( 3 . 4 . 4 2 ) 이때 ∥ A w ∥ \Vert Aw\Vert ∥ A w ∥
∥ A w ∥ 2 = ∥ A ( w 1 v 1 + w 2 v 2 ) ∥ 2 = ∥ w 1 A v 1 + w 2 A v 2 ∥ 2 = ∥ w 1 σ 1 u 1 + w 2 σ 2 u 2 ∥ 2 = ∥ w 1 σ 1 u 1 ∥ 2 + ∥ w 2 σ 2 u 2 ∥ 2 (orthogonal) = w 1 2 σ 1 2 ∥ u 1 ∥ 2 + w 2 2 σ 2 2 ∥ u 2 ∥ 2 = w 1 2 σ 1 2 + w 2 2 σ 2 2 (unit vector) (3.4.43) \begin{aligned} \Vert Aw\Vert^2 &= \Vert A(w_{1} v_1 + w_{2} v_2)\Vert^2 \\ &= \Vert w_{1}Av_1 + w_{2}Av_2 \Vert^2 \\ &= \Vert w_{1} \sigma_1 u_1 + w_{2} \sigma_2 u_2 \Vert^2 \\ &= \Vert w_{1} \sigma_1 u_1 \Vert^2 + \Vert w_{2} \sigma_2 u_2 \Vert^2 \;\; \text{(orthogonal)} \\ &= w_{1}^2 \sigma_1^2 \Vert u_1 \Vert^2 + w_{2}^2 \sigma_2^2 \Vert u_2 \Vert^2 \\ &= w_{1}^2 \sigma_1^2 + w_{2}^2 \sigma_2^2 \;\; \text{(unit vector)}\\ \end{aligned} \tag{3.4.43} ∥ A w ∥ 2 = ∥ A ( w 1 v 1 + w 2 v 2 ) ∥ 2 = ∥ w 1 A v 1 + w 2 A v 2 ∥ 2 = ∥ w 1 σ 1 u 1 + w 2 σ 2 u 2 ∥ 2 = ∥ w 1 σ 1 u 1 ∥ 2 + ∥ w 2 σ 2 u 2 ∥ 2 (orthogonal) = w 1 2 σ 1 2 ∥ u 1 ∥ 2 + w 2 2 σ 2 2 ∥ u 2 ∥ 2 = w 1 2 σ 1 2 + w 2 2 σ 2 2 (unit vector) ( 3 . 4 . 4 3 ) σ 1 > σ 2 > 0 \sigma_1 > \sigma_2 > 0 σ 1 > σ 2 > 0 w 1 2 + w 2 2 = 1 w_{1}^2 + w_{2}^2 = 1 w 1 2 + w 2 2 = 1 w 1 , w 2 w_{1}, w_{2} w 1 , w 2
w 1 = 1 , w 2 = 0 (3.4.44) w_{1} = 1, w_{2} = 0 \tag{3.4.44} w 1 = 1 , w 2 = 0 ( 3 . 4 . 4 4 ) 이다. 즉, 첫 번째 오른쪽 특이벡터 방향으로 하는 것이다.
w = v 1 (3.4.45) w = v_1 \tag{3.4.45} w = v 1 ( 3 . 4 . 4 5 ) 이때 ∥ A w ∥ \Vert Aw\Vert ∥ A w ∥
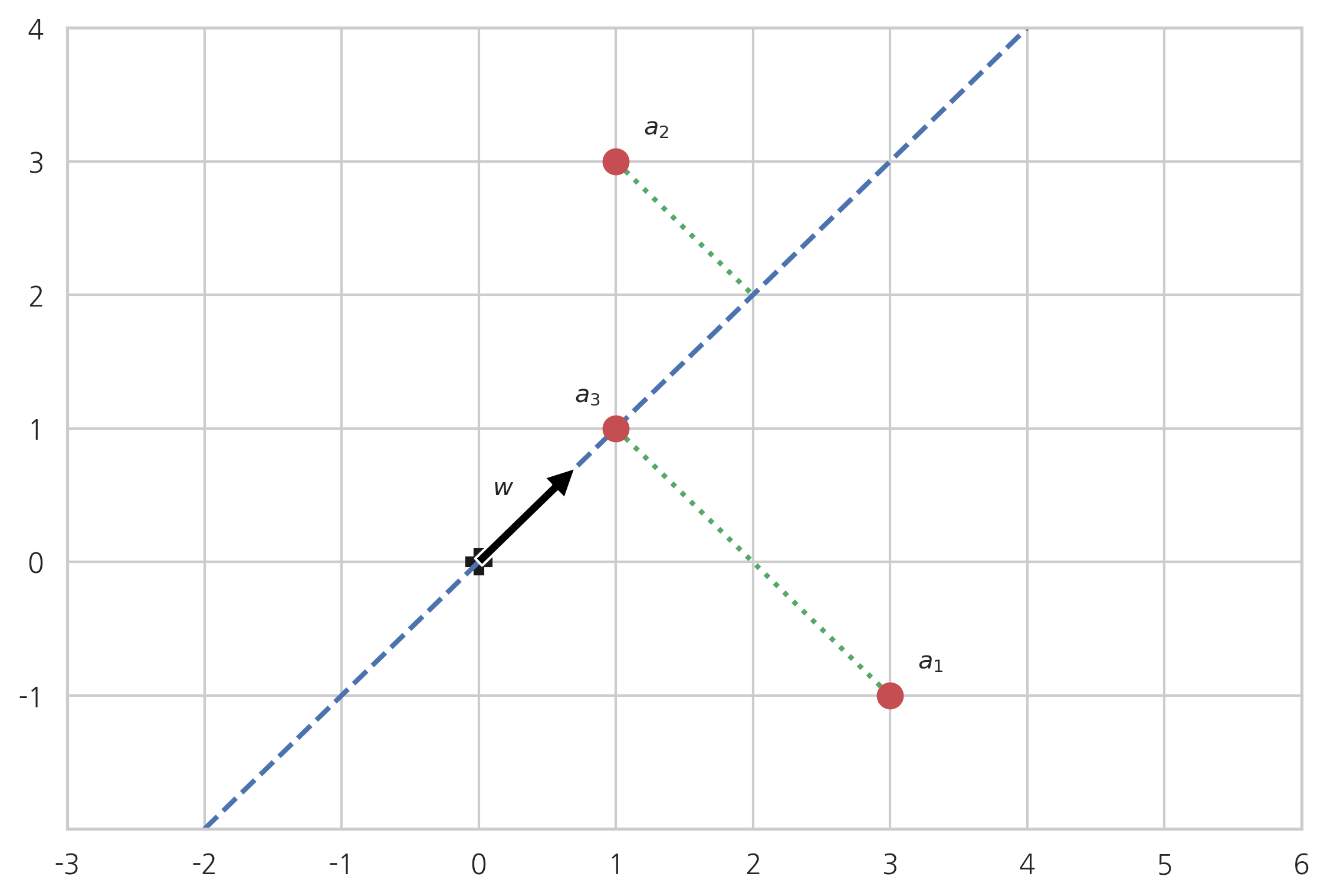
∥ A w ∥ = ∥ A v 1 ∥ = ∥ σ 1 u 1 ∥ = σ 1 ∥ u 1 ∥ = σ 1 (3.4.46) \Vert Aw\Vert = \Vert Av_1\Vert = \Vert \sigma_1 u_1\Vert = \sigma_1 \Vert u_1\Vert = \sigma_1 \tag{3.4.46} ∥ A w ∥ = ∥ A v 1 ∥ = ∥ σ 1 u 1 ∥ = σ 1 ∥ u 1 ∥ = σ 1 ( 3 . 4 . 4 6 ) 위에서 예로 들었던 행렬
A = [ 3 − 1 1 3 1 1 ] (3.4.47) A = \begin{bmatrix} 3 & -1 \\ 1 & 3 \\ 1 & 1 \end{bmatrix} \tag{3.4.47} A = ⎣ ⎢ ⎡ 3 1 1 − 1 3 1 ⎦ ⎥ ⎤ ( 3 . 4 . 4 7 ) 첫 번째 오른쪽 특이벡터
v 1 = [ 2 2 2 2 ] (3.4.48) v_1 = \begin{bmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \\ \end{bmatrix} \tag{3.4.48} v 1 = [ 2 2 2 2 ] ( 3 . 4 . 4 8 ) 가 가장 거리의 합이 작은 방향이 된다. 그리고 이때의 거리의 제곱의 합은 다음과 같다.
∥ A ∥ 2 − ∥ A w ∥ 2 = ∥ A ∥ 2 − σ 1 2 (3.4.49) \Vert A \Vert^2 - \Vert Aw\Vert^2 =\Vert A \Vert^2 - \sigma_1^2 \tag{3.4.49} ∥ A ∥ 2 − ∥ A w ∥ 2 = ∥ A ∥ 2 − σ 1 2 ( 3 . 4 . 4 9 ) np. linalg. norm( A) ** 2 - S[ 0 ] ** 2 9.999999999999998
w = np. array( [ 1 , 1 ] ) / np. sqrt( 2 )
a1 = np. array( [ 3 , - 1 ] )
a2 = np. array( [ 1 , 3 ] )
a3 = np. array( [ 1 , 1 ] )
black = { "facecolor" : "black" }
plt. figure( figsize= ( 9 , 6 ) )
plt. plot( 0 , 0 , 'kP' , ms= 10 )
plt. annotate( '' , xy= w, xytext= ( 0 , 0 ) , arrowprops= black)
plt. plot( [ - 2 , 4 ] , [ - 2 , 4 ] , 'b--' , lw= 2 )
plt. plot( [ a1[ 0 ] , 1 ] , [ a1[ 1 ] , 1 ] , 'g:' , lw= 2 )
plt. plot( [ a2[ 0 ] , 2 ] , [ a2[ 1 ] , 2 ] , 'g:' , lw= 2 )
plt. plot( a1[ 0 ] , a1[ 1 ] , 'ro' , ms= 10 )
plt. plot( a2[ 0 ] , a2[ 1 ] , 'ro' , ms= 10 )
plt. plot( a3[ 0 ] , a3[ 1 ] , 'ro' , ms= 10 )
plt. text( 0.1 , 0.5 , "$w$" )
plt. text( a1[ 0 ] + 0.2 , a1[ 1 ] + 0.2 , "$a_1$" )
plt. text( a2[ 0 ] + 0.2 , a2[ 1 ] + 0.2 , "$a_2$" )
plt. text( a3[ 0 ] - 0.3 , a3[ 1 ] + 0.2 , "$a_3$" )
plt. xticks( np. arange( - 3 , 15 ) )
plt. yticks( np. arange( - 1 , 5 ) )
plt. xlim( - 3 , 6 )
plt. ylim( - 2 , 4 )
plt. show( )
일반적인 풀이
만약 N = 3 N=3 N = 3
∥ A w ∥ 2 = ∑ i = 1 N ( a i T w ) 2 = ∑ i = 1 N ( a i T w ) T ( a i T w ) = ∑ i = 1 N w T a i a i T w = w T ( ∑ i = 1 N a i a i T ) w = w T A T A w (3.4.50) \begin{aligned} \Vert Aw \Vert^2 &= \sum_{i=1}^{N} (a_i^Tw)^2 \\ &= \sum_{i=1}^{N} (a_i^Tw)^T(a_i^Tw) \\ &= \sum_{i=1}^{N} w^Ta_ia_i^Tw \\ &= w^T \left( \sum_{i=1}^{N} a_ia_i^T \right) w \\ &= w^T A^TA w \\ \end{aligned} \tag{3.4.50} ∥ A w ∥ 2 = i = 1 ∑ N ( a i T w ) 2 = i = 1 ∑ N ( a i T w ) T ( a i T w ) = i = 1 ∑ N w T a i a i T w = w T ( i = 1 ∑ N a i a i T ) w = w T A T A w ( 3 . 4 . 5 0 ) 분산행렬의 고유분해 공식을 이용하면,
w T A T A w = w T V Λ V T w = w T ( ∑ i = 1 M σ i 2 v i v i T ) w = ∑ i = 1 M σ i 2 ( w T v i ) ( v i T w ) = ∑ i = 1 M σ i 2 ∥ v i T w ∥ 2 (3.4.51) \begin{aligned} w^T A^TA w &= w^T V \Lambda V^T w \\ &= w^T \left( \sum_{i=1}^{M} \sigma^2_iv_iv_i^T \right) w \\ &= \sum_{i=1}^{M}\sigma^2_i(w^Tv_i)(v_i^Tw) \\ &= \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw\Vert^2 \\ \end{aligned} \tag{3.4.51} w T A T A w = w T V Λ V T w = w T ( i = 1 ∑ M σ i 2 v i v i T ) w = i = 1 ∑ M σ i 2 ( w T v i ) ( v i T w ) = i = 1 ∑ M σ i 2 ∥ v i T w ∥ 2 ( 3 . 4 . 5 1 ) 이 된다. 이 식에서 M M M
즉, 우리가 풀어야 할 문제는 다음과 같다.
arg max w ∥ A w ∥ 2 = arg max w ∑ i = 1 M σ i 2 ∥ v i T w ∥ 2 (3.4.52) \arg\max_w \Vert Aw \Vert^2 = \arg\max_w \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw\Vert^2 \tag{3.4.52} arg w max ∥ A w ∥ 2 = arg w max i = 1 ∑ M σ i 2 ∥ v i T w ∥ 2 ( 3 . 4 . 5 2 ) 이 값을 가장 크게 하려면 w w w v 1 v_1 v 1
랭크-1 근사문제
또 a i a_i a i w w w
a i ∥ w = ( a i T w ) w (3.4.53) a^{\Vert w}_i = (a_i^Tw)w \tag{3.4.53} a i ∥ w = ( a i T w ) w ( 3 . 4 . 5 3 ) 이므로 w w w N N N M M M a 1 , a 2 , ⋯ , a N ( a i ∈ R M ) a_1, a_2, \cdots, a_N\;(a_i \in \mathbf{R}^M) a 1 , a 2 , ⋯ , a N ( a i ∈ R M ) N N N a 1 ∥ w , a 2 ∥ w , ⋯ , a N ∥ w ( a i ∥ w ∈ R 1 ) a^{\Vert w}_1, a^{\Vert w}_2, \cdots, a^{\Vert w}_N\;(a^{\Vert w}_i \in \mathbf{R}^1) a 1 ∥ w , a 2 ∥ w , ⋯ , a N ∥ w ( a i ∥ w ∈ R 1 )
A ′ = [ ( a 1 ∥ w ) T ( a 2 ∥ w ) T ⋮ ( a N ∥ w ) T ] = [ a 1 T w w T a 2 T w w T ⋮ a N T w w T ] = [ a 1 T a 2 T ⋮ a N T ] w w T = A w w T (3.4.54) A'= \begin{bmatrix} \left(a^{\Vert w}_1\right)^T \\ \left(a^{\Vert w}_2\right)^T \\ \vdots \\ \left(a^{\Vert w}_N\right)^T \end{bmatrix} = \begin{bmatrix} a_1^Tw^{}w^T \\ a_2^Tw^{}w^T \\ \vdots \\ a_N^Tw^{}w^T \end{bmatrix} = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_N^T \end{bmatrix} w^{}w^T = Aw^{}w^T \tag{3.4.54} A ′ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ( a 1 ∥ w ) T ( a 2 ∥ w ) T ⋮ ( a N ∥ w ) T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 T w w T a 2 T w w T ⋮ a N T w w T ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 T a 2 T ⋮ a N T ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ w w T = A w w T ( 3 . 4 . 5 4 ) 이 답은 원래 행렬 A A A w w T w^{}w^T w w T A A A A ′ A' A ′
arg min w ∥ A − A ′ ∥ = arg min w ∥ A − A w w T ∥ (3.4.55) \arg\min_w \Vert A - A' \Vert = \arg\min_w \Vert A^{} - A^{}w^{}w^T \Vert \tag{3.4.55} arg w min ∥ A − A ′ ∥ = arg w min ∥ A − A w w T ∥ ( 3 . 4 . 5 5 ) 따라서 문제를 랭크-1 근사문제(rank-1 approximation problem) 라고도 한다.
K K K 이번에는 N N N M M M a 1 , a 2 , ⋯ , a N ( a i ∈ R M ) a_1, a_2, \cdots, a_N\;(a_i \in \mathbf{R}^M) a 1 , a 2 , ⋯ , a N ( a i ∈ R M ) w 1 , w 2 , ⋯ , w K w_1, w_2, \cdots, w_K w 1 , w 2 , ⋯ , w K K K K N N N K K K a 1 ∥ w , a 2 ∥ w , ⋯ , a N ∥ w a^{\Vert w}_1, a^{\Vert w}_2, \cdots, a^{\Vert w}_N\; a 1 ∥ w , a 2 ∥ w , ⋯ , a N ∥ w w 1 , w 2 , ⋯ , w K w_1, w_2, \cdots, w_K w 1 , w 2 , ⋯ , w K K K K
기저벡터행렬을 W W W
W = [ w 1 w 2 ⋯ w K ] (3.4.56) W = \begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix} \tag{3.4.56} W = [ w 1 w 2 ⋯ w K ] ( 3 . 4 . 5 6 ) 정규직교 기저벡터에 대한 벡터 a i a_i a i a i ∥ w a^{\Vert w}_i a i ∥ w
a i ∥ w = ( a i T w 1 ) w 1 + ( a i T w 2 ) w 2 + ⋯ + ( a i T w K ) w K = ∑ k = 1 K ( a i T w k ) w k (3.4.57) \begin{aligned} a^{\Vert w}_i &= (a_i^Tw_1)w_1 + (a_i^Tw_2)w_2 + \cdots + (a_i^Tw_K)w_K \\ \end{aligned} = \sum_{k=1}^K (a_i^Tw_k)w_k \tag{3.4.57} a i ∥ w = ( a i T w 1 ) w 1 + ( a i T w 2 ) w 2 + ⋯ + ( a i T w K ) w K = k = 1 ∑ K ( a i T w k ) w k ( 3 . 4 . 5 7 ) 벡터 a 1 , a 2 , ⋯ , a N a_1, a_2, \cdots, a_N a 1 , a 2 , ⋯ , a N A A A
A = [ a 1 T a 2 T ⋮ a N T ] (3.4.58) A = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_N^T \end{bmatrix} \tag{3.4.58} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 T a 2 T ⋮ a N T ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ( 3 . 4 . 5 8 ) 모든 점들과의 거리의 제곱의 합은 다음처럼 행렬의 놈으로 계산할 수 있다.
∑ i = 1 N ∥ a i ⊥ w ∥ 2 = ∑ i = 1 N ∥ a i ∥ 2 − ∑ i = 1 N ∥ a i ∥ w ∥ 2 = ∥ A ∥ 2 − ∑ i = 1 N ∥ a i ∥ w ∥ 2 (3.4.59) \begin{aligned} \sum_{i=1}^N \Vert a_i^{\perp w}\Vert^2 &= \sum_{i=1}^N \Vert a_i\Vert^2 - \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 \\ &= \Vert A \Vert^2 - \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 \\ \end{aligned} \tag{3.4.59} i = 1 ∑ N ∥ a i ⊥ w ∥ 2 = i = 1 ∑ N ∥ a i ∥ 2 − i = 1 ∑ N ∥ a i ∥ w ∥ 2 = ∥ A ∥ 2 − i = 1 ∑ N ∥ a i ∥ w ∥ 2 ( 3 . 4 . 5 9 ) 행렬 A A A
두 번째 항은 K=1일 때와 같은 방법으로 분산행렬 형태로 바꿀 수 있다.
∑ i = 1 N ∥ a i ∥ w ∥ 2 = ∑ i = 1 N ∑ k = 1 K ∥ ( a i T w k ) w k ∥ 2 = ∑ i = 1 N ∑ k = 1 K ∥ a i T w k ∥ 2 = ∑ k = 1 K w k T A T A w k (3.4.60) \begin{aligned} \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 &= \sum_{i=1}^N \sum_{k=1}^K \Vert (a_i^Tw_k)w_k \Vert^2 \\ &= \sum_{i=1}^N \sum_{k=1}^K \Vert a_i^Tw_k \Vert^2 \\ &= \sum_{k=1}^K w_k^T A^TA w_k \\ \end{aligned} \tag{3.4.60} i = 1 ∑ N ∥ a i ∥ w ∥ 2 = i = 1 ∑ N k = 1 ∑ K ∥ ( a i T w k ) w k ∥ 2 = i = 1 ∑ N k = 1 ∑ K ∥ a i T w k ∥ 2 = k = 1 ∑ K w k T A T A w k ( 3 . 4 . 6 0 ) 분산행렬의 고유분해를 사용하면
∑ k = 1 K w k T A T A w k = ∑ k = 1 K w k T V Λ V T w k = ∑ k = 1 K w k T ( ∑ i = 1 M σ i 2 v i v i T ) w k = ∑ k = 1 K ∑ i = 1 M σ i 2 ∥ v i T w k ∥ 2 (3.4.61) \begin{aligned} \sum_{k=1}^K w_k^T A^TA w_k &= \sum_{k=1}^K w_k^T V \Lambda V^T w_k \\ &= \sum_{k=1}^K w_k^T \left( \sum_{i=1}^{M} \sigma^2_iv_iv_i^T \right) w_k \\ &= \sum_{k=1}^K \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw_k\Vert^2 \\ \end{aligned} \tag{3.4.61} k = 1 ∑ K w k T A T A w k = k = 1 ∑ K w k T V Λ V T w k = k = 1 ∑ K w k T ( i = 1 ∑ M σ i 2 v i v i T ) w k = k = 1 ∑ K i = 1 ∑ M σ i 2 ∥ v i T w k ∥ 2 ( 3 . 4 . 6 1 ) 이 문제도 1차원 근사문제처럼 풀면 다음과 같은 답을 얻을 수 있다.
가장 큰 K K K
랭크-K 근사문제
우리가 찾아야 하는 것은 이 값을 가장 크게 하는 K K K w k w_k w k 오른쪽 기저벡터 중 가장 큰 K K K
이 문제는 다음처럼 랭크-K K K
a i ∥ w = ( a i T w 1 ) w 1 + ( a i T w 2 ) w 2 + ⋯ + ( a i T w K ) w K = [ w 1 w 2 ⋯ w K ] [ a i T w 1 a i T w 2 ⋮ a i T w K ] = [ w 1 w 2 ⋯ w K ] [ w 1 T w 2 T ⋮ w K T ] a i = W W T a i (3.4.62) \begin{aligned} a^{\Vert w}_i &= (a_i^Tw_1)w_1 + (a_i^Tw_2)w_2 + \cdots + (a_i^Tw_K)w_K \\ &= \begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix} \begin{bmatrix} a_i^Tw_1 \\ a_i^Tw_2 \\ \vdots \\ a_i^Tw_K \end{bmatrix} \\ &= \begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix} \begin{bmatrix} w_1^T \\ w_2^T \\ \vdots \\ w_K^T \end{bmatrix} a_i \\ &= WW^Ta_i \end{aligned} \tag{3.4.62} a i ∥ w = ( a i T w 1 ) w 1 + ( a i T w 2 ) w 2 + ⋯ + ( a i T w K ) w K = [ w 1 w 2 ⋯ w K ] ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a i T w 1 a i T w 2 ⋮ a i T w K ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = [ w 1 w 2 ⋯ w K ] ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ w 1 T w 2 T ⋮ w K T ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ a i = W W T a i ( 3 . 4 . 6 2 ) 이러한 투영벡터를 모아놓은 행렬 A ′ A' A ′
A ′ = [ ( a 1 ∥ w ) T ( a 2 ∥ w ) T ⋮ ( a N ∥ w ) T ] = [ a 1 T W W T a 2 T W W T ⋮ a N T W W T ] = [ a 1 T a 2 T ⋮ a N T ] W W T = A W W T (3.4.63) A'= \begin{bmatrix} \left(a^{\Vert w}_1\right)^T \\ \left(a^{\Vert w}_2\right)^T \\ \vdots \\ \left(a^{\Vert w}_N\right)^T \end{bmatrix} = \begin{bmatrix} a_1^TW^{}W^T \\ a_2^TW^{}W^T\\ \vdots \\ a_N^TW^{}W^T \end{bmatrix} = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_N^T \end{bmatrix} W^{}W^T = AW^{}W^T \tag{3.4.63} A ′ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ( a 1 ∥ w ) T ( a 2 ∥ w ) T ⋮ ( a N ∥ w ) T ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 T W W T a 2 T W W T ⋮ a N T W W T ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 T a 2 T ⋮ a N T ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ W W T = A W W T ( 3 . 4 . 6 3 ) 따라서 이 문제는 원래 행렬 A A A W W T W_{}W^T W W T A A A A ′ A' A ′
arg min w 1 , ⋯ , w K ∥ A − A W W T ∥ (3.4.64) \arg\min_{w_1,\cdots,w_K} \Vert A - AW^{}W^T \Vert \tag{3.4.64} arg w 1 , ⋯ , w K min ∥ A − A W W T ∥ ( 3 . 4 . 6 4 )