[Linear algebra] 3.1 선형대수와 해석기하의 기초

JKH·2024년 10월 16일
Data ScienceLinear AlgebraMathematicspython
0

선형대수

목록 보기
5/12

데이터 사이언스 스쿨 에서 공부한 내용입니다.

3.1 선형대수와 해석기하의 기초

선형대수는 숫자 데이터의 계산에만 사용되는 것이 아니다. 직선과 화살표, 이미지 등을 다루는 기하학에서도 선형대수는 중요한 역할을 한다. 이 절에서는 선형대수를 기하학에서 어떻게 응용하고 선형대수의 연산이 기하학적으로 어떤 의미를 가지는지 알아본다.

벡터의 기하학적 의미

NN차원 벡터 aa는 NN차원의 공간에서

  • 벡터 aa의 값으로 표시되는 점(point) 또는

  • 원점과 벡터 aa의 값으로 표시되는 점을 연결한 화살표(arrow)

라고 생각할 수 있다.

예를 들어 2차원 벡터

a=[a1a2](3.1.1)a = \begin{bmatrix}a_1 \\ a_2 \end{bmatrix} \tag{3.1.1}

는 2차원 공간에서 xx 좌표가 a1a_1, yy 좌표가 a2a_2인 점으로 생각할 수도 있고 또는 원점에서 이 점을 가리키는 화살표로 생각할 수도 있다. 벡터를 화살표로 생각하는 경우에는 길이와 방향을 고정시킨 채 평행이동할 수 있다.

(앞으로 나오는 그림은 모두 맷플롯리브 패키지로 그린 그림이다. 이 코드는 파이썬으로 이러한 그림도 제작할 수 있다는 것을 보이기 위한 것일 뿐 이번 절의 내용과는 관계없으므로 그림 코드의 내용은 무시해도 된다.) 

import numpy as np
import matplotlib.pylab as plt

plt.rc("font", size=18)  # 그림의 폰트 크기를 18로 고정
gray = {"facecolor": "gray"}
black = {"facecolor": "black"}
red = {"facecolor": "red"}
green = {"facecolor": "green"}
blue = {"facecolor": "blue"}
a = np.array([1, 2])
plt.plot(0, 0, 'kP', ms=20)
plt.plot(a[0], a[1], 'ro', ms=20)
plt.annotate('', xy=[-0.6, 1.6], xytext=(0.2, 0.7), arrowprops=gray)
plt.annotate('', xy=a, xytext=(0, 0), arrowprops=black)
plt.annotate('', xy=a + [-1, 1], xytext=(-1, 1), arrowprops=black)
plt.text(0.35, 1.15, "$a$")
plt.text(1.15, 2.25, "$(1,2)$")
plt.text(-0.7, 2.1, "$a$")
plt.text(-0.9, 0.6, "평행이동")
plt.xticks(np.arange(-2, 4))
plt.yticks(np.arange(-1, 4))
plt.xlim(-2.4, 3.4)
plt.ylim(-0.8, 3.4)
plt.show()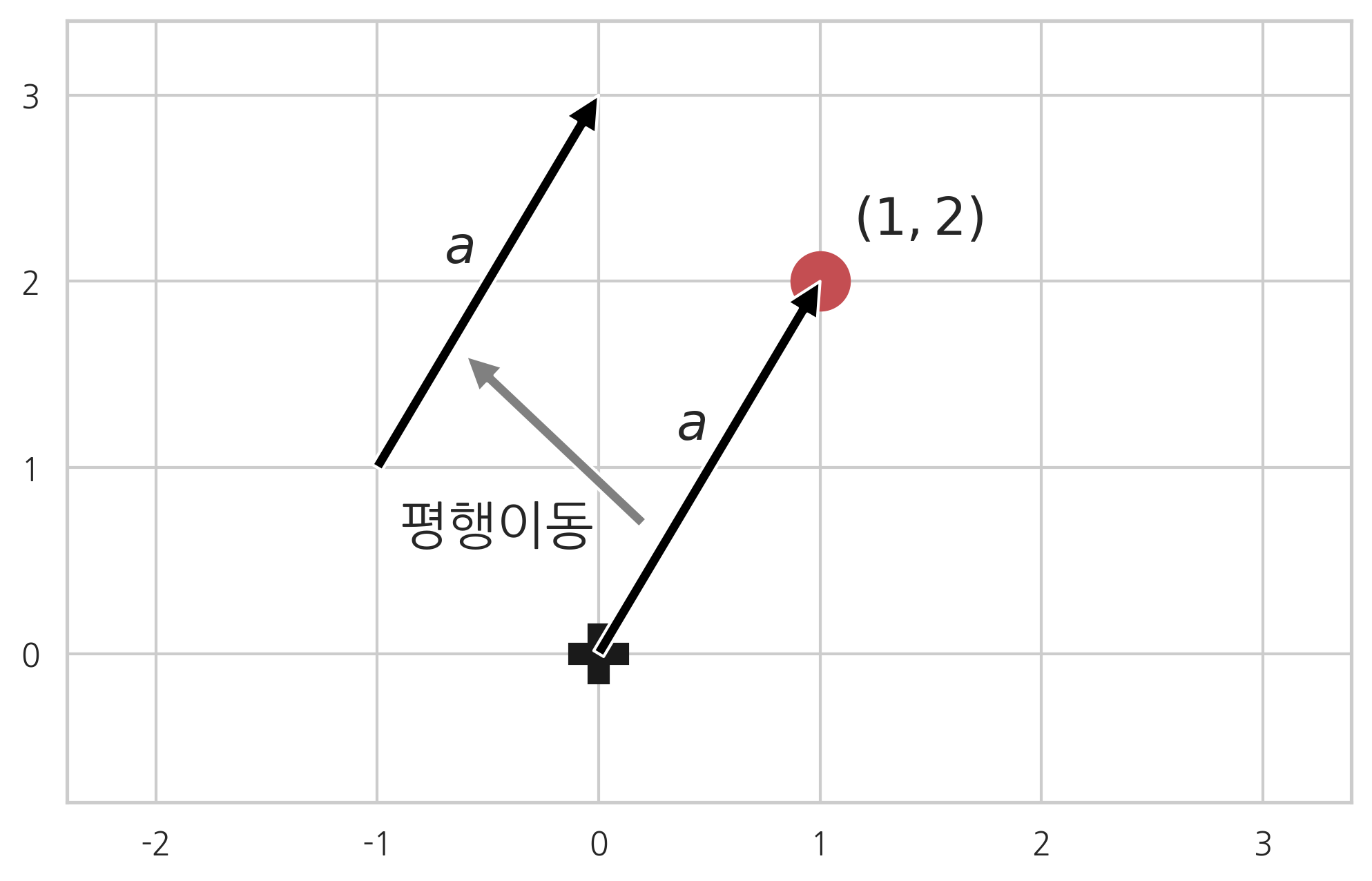

벡터의 길이

벡터 aa의 길이는 놈(norm) ∥a∥\| a \|으로 정의한다.

∥a∥=aTa=a12+⋯+aN2(3.1.2)\| a \| = \sqrt{a^T a } = \sqrt{a_1^2 + \cdots + a_N^2} \tag{3.1.2}

넘파이 linalg 서브 패키지의 norm() 명령으로 벡터의 길이를 계산할 수 있다. 위에서 예로 든 2차원 벡터 a=[a1    a2]Ta = [a_1 \;\; a_2]^T의 길이는 5≈2.236\sqrt{5} \approx 2.236이다.

a = np.array([1, 2])
np.linalg.norm(a)
2.23606797749979

스칼라와 벡터의 곱

양의 실수와 벡터를 곱하면 벡터의 방향은 변하지 않고 실수의 크기만큼 벡터의 길이가 커진다. 만약 음의 실수를 곱하면 벡터의 방향이 반대가 된다.

a = np.array([1, 2])
b = 2 * a
c = -a
plt.annotate('', xy=b, xytext=(0, 0), arrowprops=red)
plt.text(0.8, 3.1, "$2a$")
plt.text(2.2, 3.8, "$(2, 4)$")
plt.annotate('', xy=a, xytext=(0, 0), arrowprops=gray)
plt.text(0.1, 1.3, "$a$")
plt.text(1.1, 1.4, "$(1, 2)$")
plt.plot(c[0], c[1], 'ro', ms=10)
plt.annotate('', xy=c, xytext=(0, 0), arrowprops=blue)
plt.text(-1.3, -0.8, "$-a$")
plt.text(-3, -2.5, "$(-1, -2)$")
plt.plot(0, 0, 'kP', ms=20)
plt.xticks(np.arange(-5, 6))
plt.yticks(np.arange(-5, 6))
plt.xlim(-4.4, 5.4)
plt.ylim(-3.2, 5.2)
plt.show()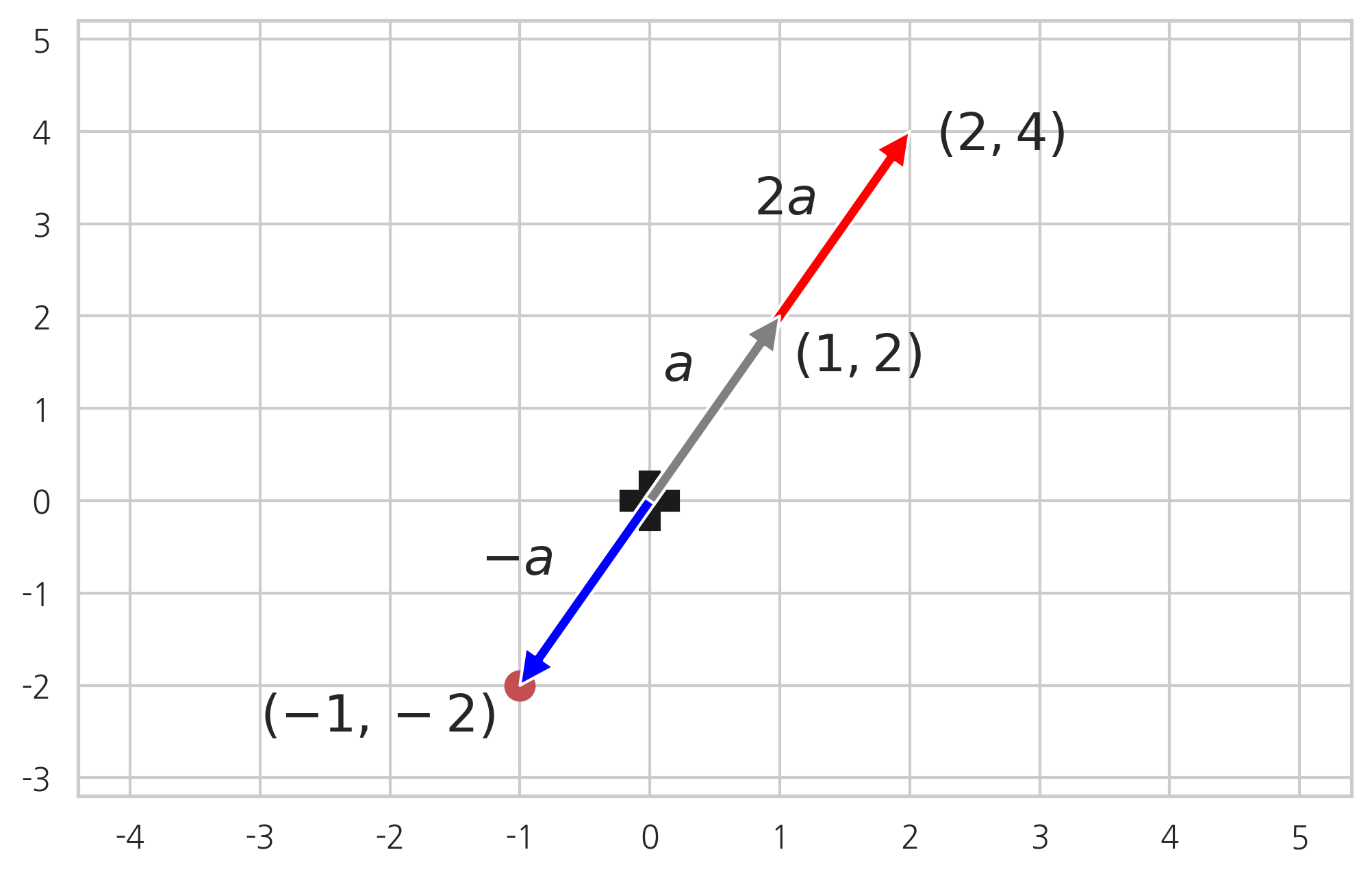

단위벡터

길이가 1인 벡터를 단위벡터(unit vector) 라고 한다. 예를 들어 다음과 같은 벡터들은 모두 단위벡터다.

a=[10],    b=[01],    c=[1212](3.1.3)a = \begin{bmatrix}1 \\ 0\end{bmatrix} ,\;\; b = \begin{bmatrix}0 \\ 1\end{bmatrix} ,\;\; c = \begin{bmatrix} \dfrac{1}{\sqrt{2}} \\ \dfrac{1}{\sqrt{2}} \end{bmatrix} \tag{3.1.3}

영벡터가 아닌 임의의 벡터 xx에 대해 다음 벡터는 벡터 xx와 같은 방향을 가리키는 단위벡터가 된다.

x∥x∥(3.1.4)\dfrac{x}{\| x \|} \tag{3.1.4}
a = np.array([1, 0])
b = np.array([0, 1])
c = np.array([1/np.sqrt(2), 1/np.sqrt(2)])
np.linalg.norm(a), np.linalg.norm(b), np.linalg.norm(c)
(1.0, 1.0, 0.9999999999999999)

벡터의 합

벡터와 벡터의 합도 벡터가 된다. 이때 두 벡터의 합은 그 두 벡터를 이웃하는 변으로 가지는 평행사변형의 대각선 벡터가 된다.

a=[12],    b=[21]      →      c=a+b=[33](3.1.5)a = \begin{bmatrix}1 \\ 2\end{bmatrix} ,\;\; b = \begin{bmatrix}2 \\ 1\end{bmatrix} \;\;\; \rightarrow \;\;\; c = a + b = \begin{bmatrix}3 \\ 3\end{bmatrix} \tag{3.1.5}
a = np.array([1, 2])
b = np.array([2, 1])
c = a + b
plt.annotate('', xy=a, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=b, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=c, xytext=(0, 0), arrowprops=black)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(a[0], a[1], 'ro', ms=10)
plt.plot(b[0], b[1], 'ro', ms=10)
plt.plot(c[0], c[1], 'ro', ms=10)
plt.plot([a[0], c[0]], [a[1], c[1]], 'k--')
plt.plot([b[0], c[0]], [b[1], c[1]], 'k--')
plt.text(0.35, 1.15, "$a$")
plt.text(1.15, 0.25, "$b$")
plt.text(1.25, 1.45, "$c$")
plt.xticks(np.arange(-2, 5))
plt.yticks(np.arange(-1, 4))
plt.xlim(-1.4, 4.4)
plt.ylim(-0.6, 3.8)
plt.show()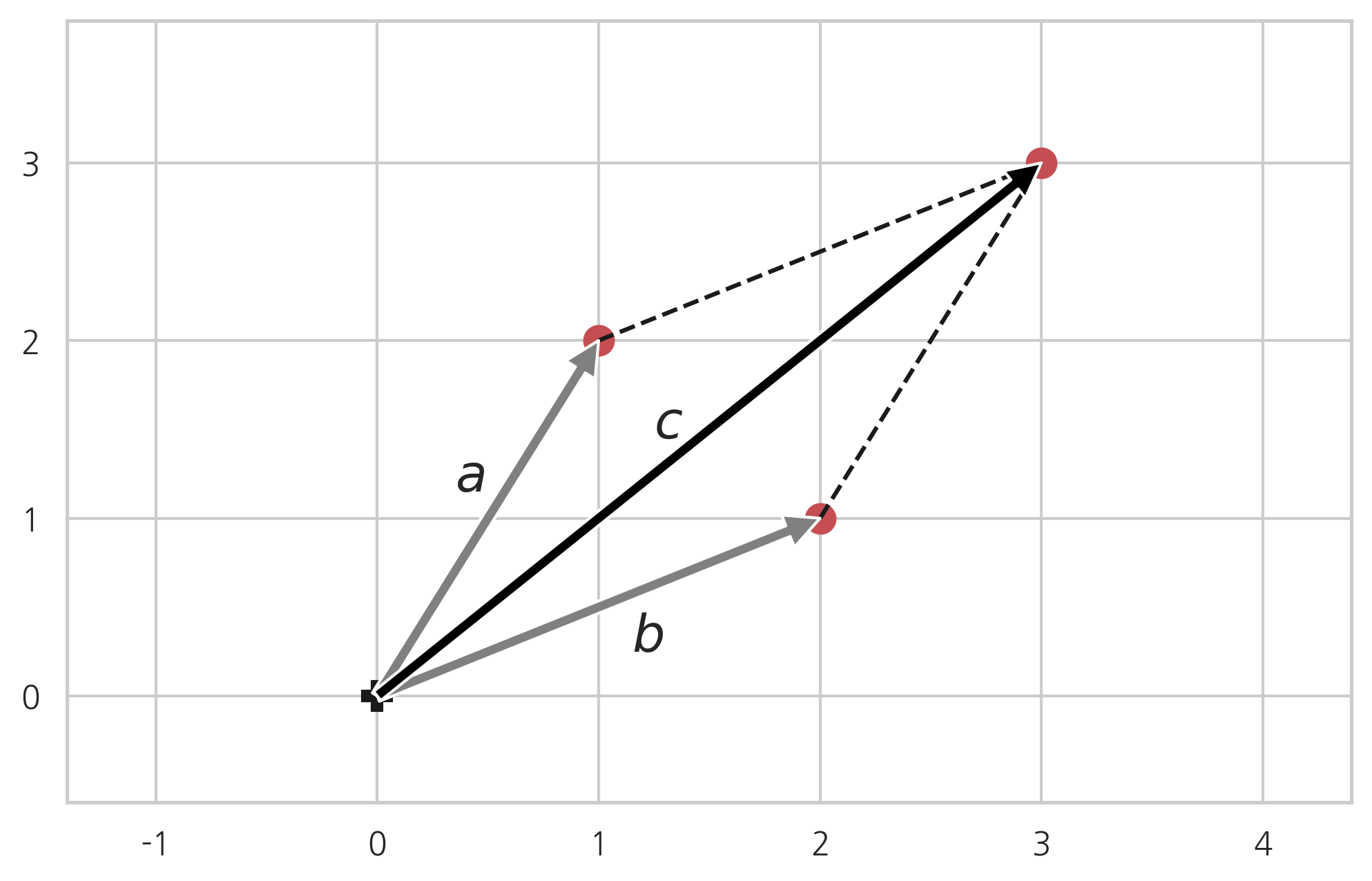

또는 벡터를 더하고자 하는 벡터의 끝점으로 평행이동했을 때 이동한 벡터가 가리키는 점의 위치로 생각할 수도 있다.

a = np.array([1, 2])
b = np.array([2, 1])
c = a + b
plt.annotate('', xy=a, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=c, xytext=a, arrowprops=gray)
plt.annotate('', xy=c, xytext=(0, 0), arrowprops=black)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(a[0], a[1], 'ro', ms=10)
plt.plot(c[0], c[1], 'ro', ms=10)
plt.text(0.35, 1.15, "$a$")
plt.text(1.45, 2.45, "$b$")
plt.text(1.25, 1.45, "$c$")
plt.xticks(np.arange(-2, 5))
plt.yticks(np.arange(-1, 4))
plt.xlim(-1.4, 4.4)
plt.ylim(-0.6, 3.8)
plt.show()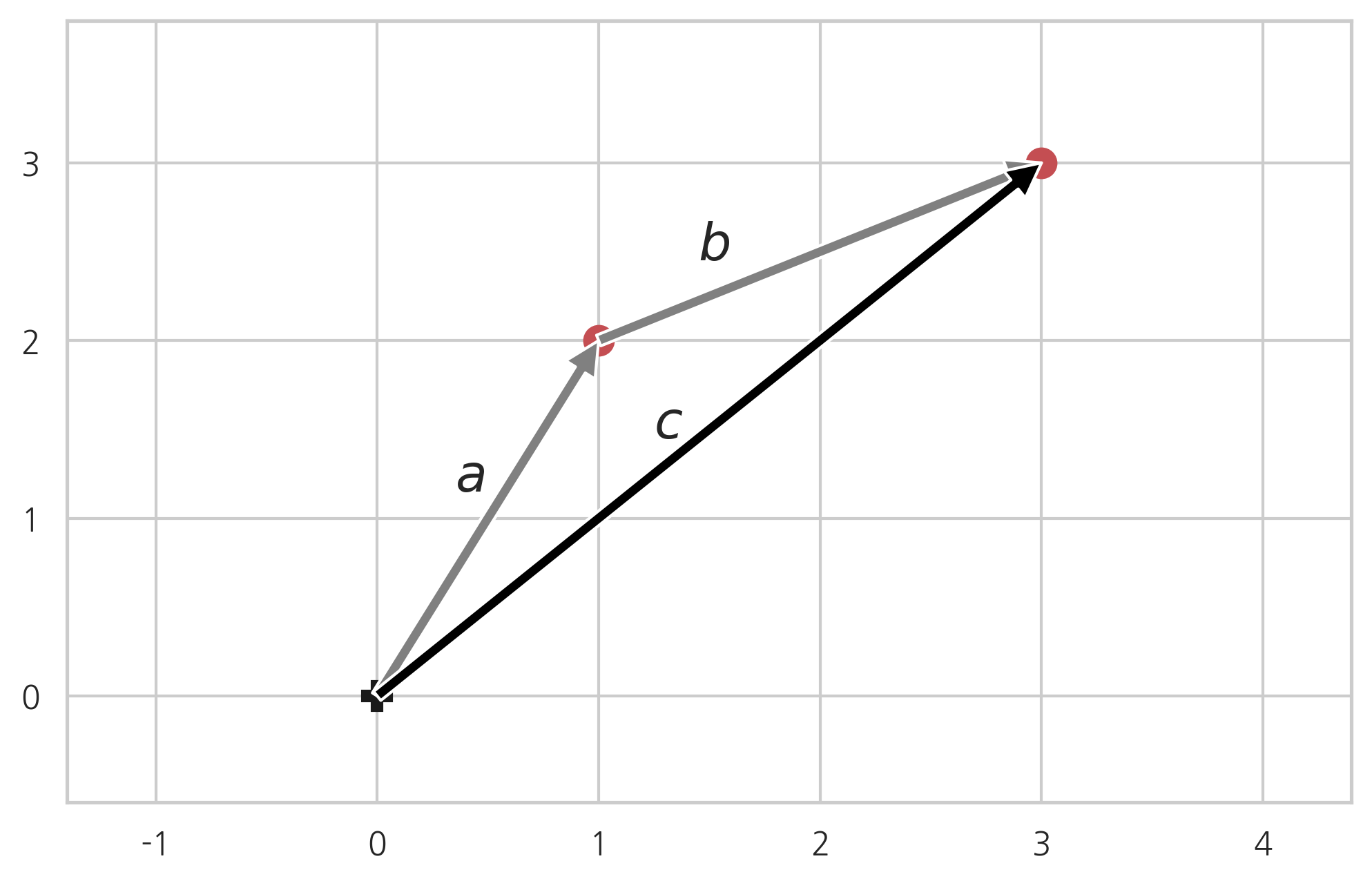

둘 중 어느 벡터를 평행이동해도 결과는 마찬가지다.

a = np.array([1, 2])
b = np.array([2, 1])
c = a + b
plt.annotate('', xy=b, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=c, xytext=b, arrowprops=gray)
plt.annotate('', xy=c, xytext=(0, 0), arrowprops=black)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(b[0], b[1], 'ro', ms=10)
plt.plot(c[0], c[1], 'ro', ms=10)
plt.text(2.45, 1.55, "$a$")
plt.text(1.25, 0.25, "$b$")
plt.text(1.25, 1.45, "$c$")
plt.xticks(np.arange(-2, 5))
plt.yticks(np.arange(-1, 4))
plt.xlim(-1.4, 4.4)
plt.ylim(-0.6, 3.8)
plt.show()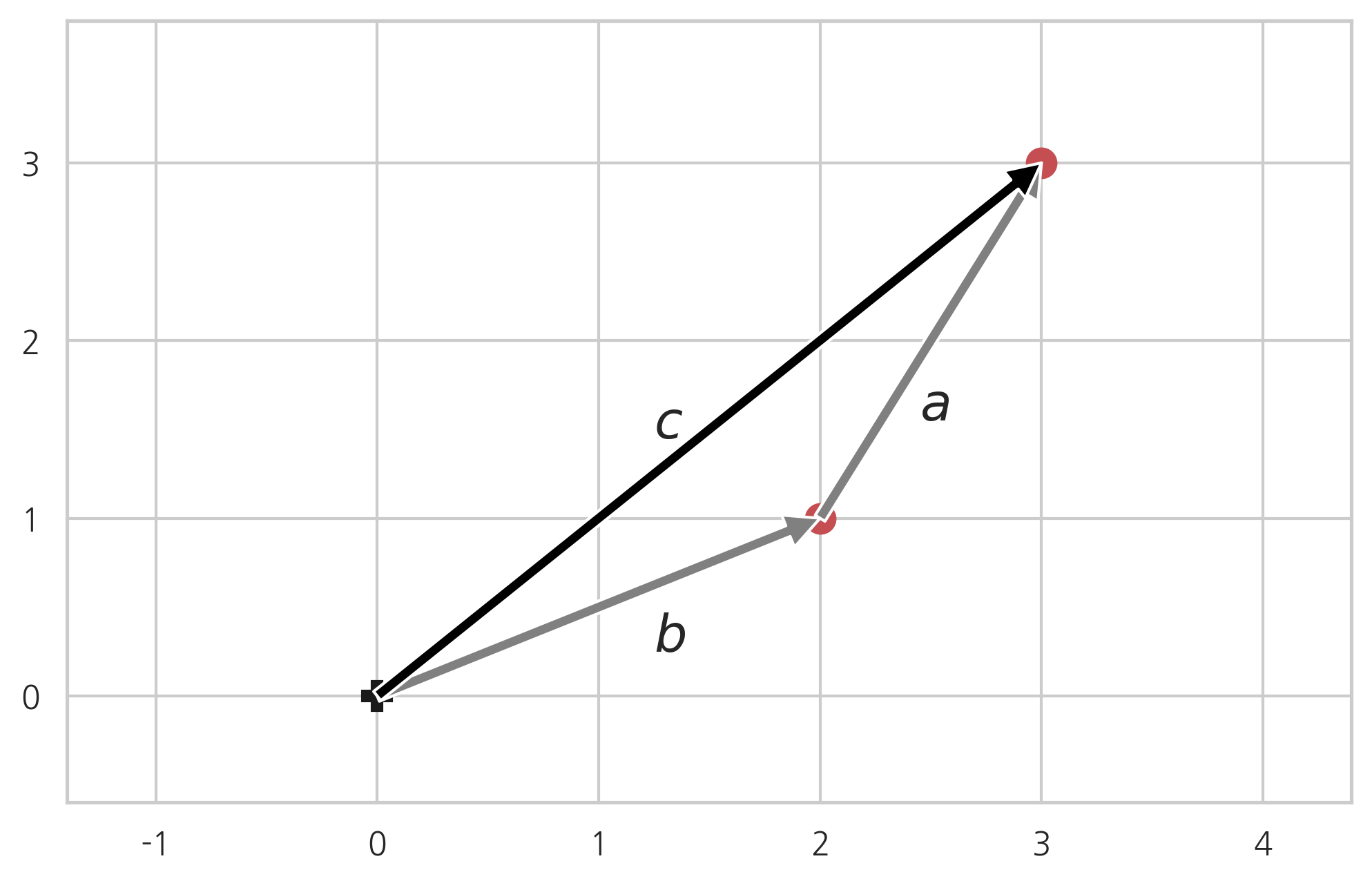

벡터의 선형조합

지금까지 벡터의 스칼라곱이 어떤 새로운 벡터가 되고 두 벡터의 합이 어떤 새로운 벡터가 되는지 살펴보았다. 여러 개의 벡터를 스칼라곱을 한 후 더한 것을 선형조합(linear combination)이라고 한다.

c1x1+c2x2+⋯+cNxN(3.1.6)c_1x_1 + c_2x_2 + \cdots + c_Nx_N \tag{3.1.6}

이 식에서 c1,⋯ ,cNc_1, \cdots, c_N은 스칼라 계수다.

x1 = np.array([1, 2])
x2 = np.array([2, 1])
x3 = 0.5 * x1 + x2
plt.annotate('', xy=0.5*x1, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=x2, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=x3, xytext=(0, 0), arrowprops=black)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(x1[0], x1[1], 'ro', ms=10)
plt.plot(x2[0], x2[1], 'ro', ms=10)
plt.plot(x3[0], x3[1], 'ro', ms=10)
plt.plot([x1[0], 0], [x1[1], 0], 'k--')
plt.text(0.6, 2.0, "$x_1$")
plt.text(-0.5, 0.5, "$0.5x_1$")
plt.text(1.15, 0.25, "$x_2$")
plt.text(2.5, 1.6, "$0.5x_1 + x_2$")
plt.xticks(np.arange(-2, 5))
plt.yticks(np.arange(-1, 4))
plt.xlim(-1.4, 4.4)
plt.ylim(-0.6, 3.8)
plt.show()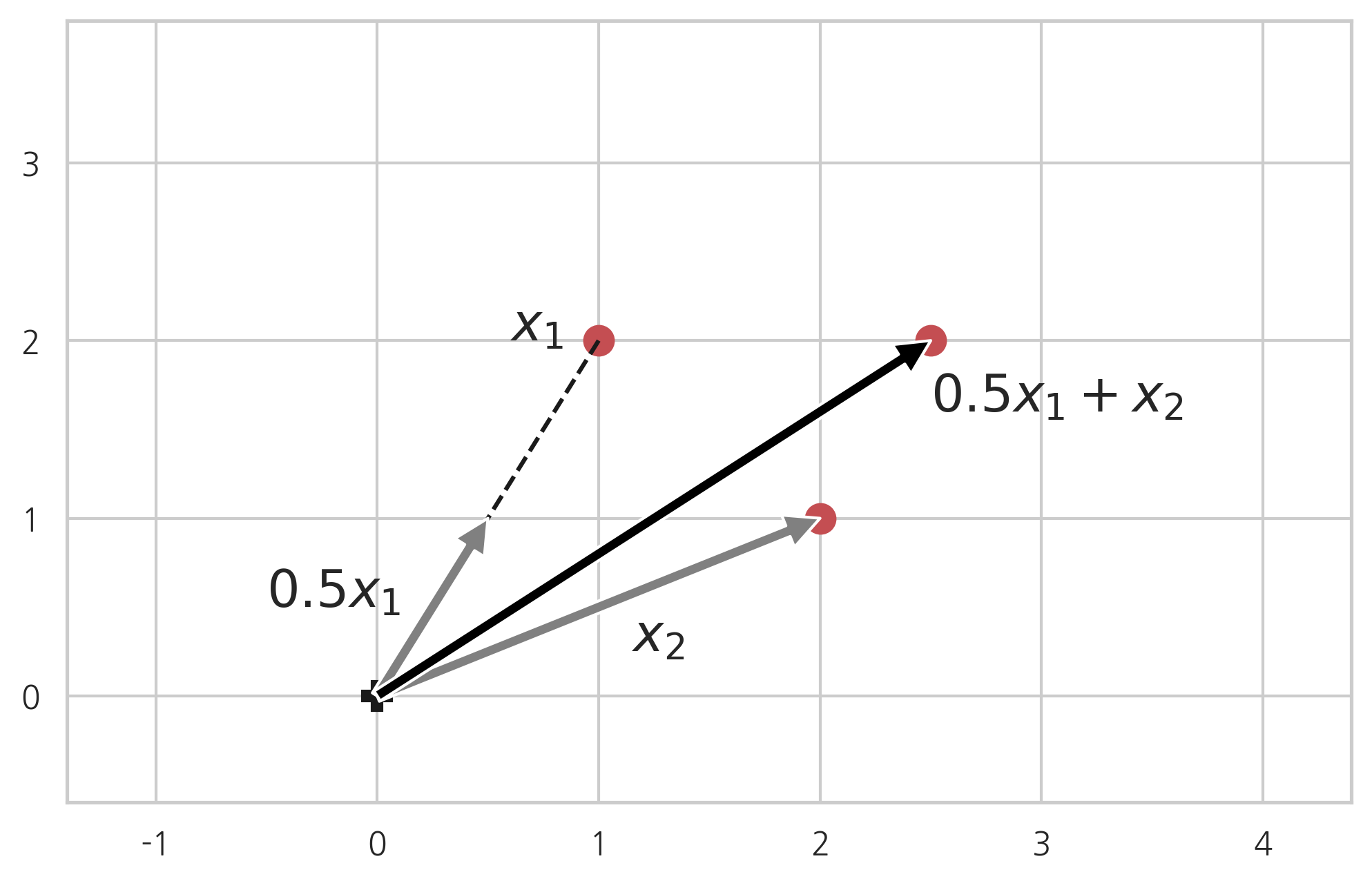

연습 문제 3.1.1

벡터 x1x_1, x2x_2가 다음과 같을 때, c1x1+c2x2c_1x_1+ c_2x_2가 다음 벡터와 같아지는 선형조합 계수 c1,c2c_1, c_2를 찾아라.

(힌트: 연립방정식의 해를 이용한다.)

x1=[12],    x2=[21](3.1.7)x_1 = \begin{bmatrix}1 \\ 2\end{bmatrix} ,\;\; x_2 = \begin{bmatrix}2 \\ 1\end{bmatrix} \tag{3.1.7}

(1)

c1x1+c2x2=[31](3.1.8)c_1x_1 + c_2x_2 = \begin{bmatrix}3 \\ 1\end{bmatrix} \tag{3.1.8}

(2)

c1x1+c2x2=[−1−1](3.1.9)c_1x_1 + c_2x_2 = \begin{bmatrix} -1 \\ -1\end{bmatrix} \tag{3.1.9}

✒️

import numpy as np
x = np.array([[1, 2], [2, 1]])
y1 = np.array([3, 1])
y2 = np.array([-1, -1])
c1 = np.linalg.solve(x, y1)
c2 = np.linalg.solve(x, y2)
c1, c2

벡터의 차

벡터의 차 a−b=ca - b = c는 벡터 bb가 가리키는 점으로부터 벡터 aa가 가리키는 점을 연결하는 벡터다. 그 이유는 벡터 bb에 벡터 a−ba-b를 더하면, 즉 벡터 bb와 벡터 a−ba-b를 연결하면 벡터 aa가 되어야 하기 때문이다.

a−b=c(3.1.10)a - b = c \tag{3.1.10}
b+c=b+(a−b)=a(3.1.11)b + c = b + (a-b) = a \tag{3.1.11}
a = np.array([1, 2])
b = np.array([2, 1])
c = a - b
plt.annotate('', xy=a, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=b, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=a, xytext=b, arrowprops=black)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(a[0], a[1], 'ro', ms=10)
plt.plot(b[0], b[1], 'ro', ms=10)
plt.text(0.35, 1.15, "$a$")
plt.text(1.15, 0.25, "$b$")
plt.text(1.55, 1.65, "$a-b$")
plt.xticks(np.arange(-2, 5))
plt.yticks(np.arange(-1, 4))
plt.xlim(-0.8, 2.8)
plt.ylim(-0.8, 2.8)
plt.show()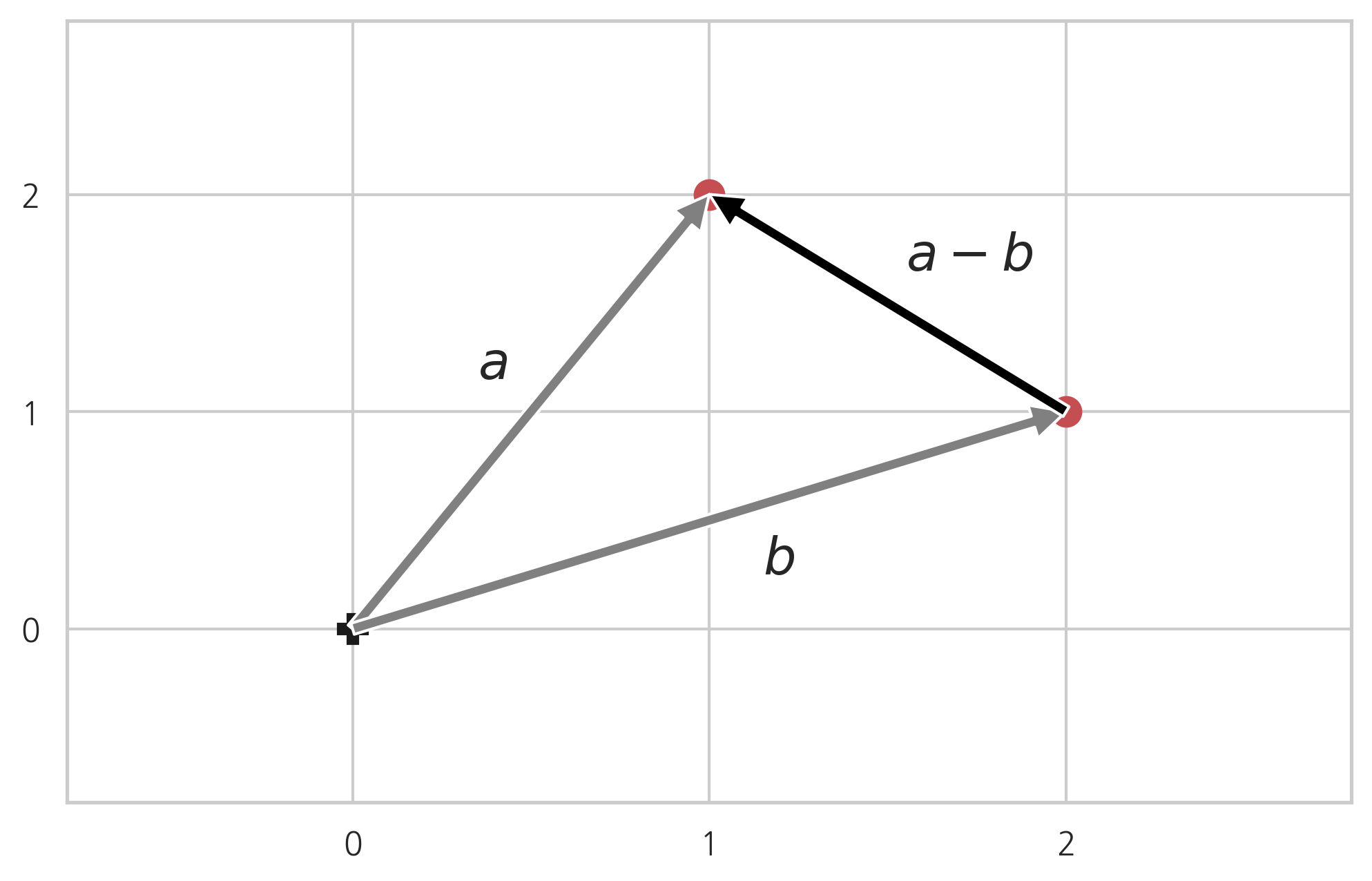

Word2Vec

나중에 인공신경망 부분에서 공부하게 될 word2vec 방법을 이용하면 단어(word)를 공간에서 점 또는 벡터(vector)로 표현할 수 있다. word2vec으로 만들어진 벡터는 단어의 의미에 따라 다음처럼 평행사변형 관계를 가질 수 있다.

일본=도쿄+(한국−서울)(3.1.12)\text{일본} = \text{도쿄} + (\text{한국} - \text{서울}) \tag{3.1.12}

한국 - 서울은 서울에서 한국으로 향하는 벡터다. 즉 의미론적으로 수도 이름을 나라 이름으로 바꾸는 행위(action) 에 비유할 수 있다. 이러한 행위를 도쿄에 대해서 적용한 결과가 도쿄 + (한국 - 서울)이다. word2vec 학습 결과에서 이렇게 계산한 위치에 가장 가까이 있는 단어를 찾으면 도쿄가 나온다.

a = np.array([2, 2])
b = np.array([3, 4])
c = np.array([4, 1])
d = a + (c - a)
e = b + (c - a)
plt.annotate('', xy=b, xytext=a, arrowprops=black)
plt.annotate('', xy=e, xytext=d, arrowprops=black)
plt.annotate('', xy=c, xytext=[0, 0], arrowprops=gray)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(a[0], a[1], 'ro', ms=10)
plt.plot(b[0], b[1], 'ro', ms=10)
plt.plot(c[0], c[1], 'ro', ms=10)
plt.text(1.6, 1.5, "서울")
plt.text(2.5, 4.3, "한국")
plt.text(3.5, 0.5, "도쿄")
plt.text(4.9, 3.2, "일본")
plt.xticks(np.arange(-2, 7))
plt.yticks(np.arange(-1, 6))
plt.xlim(-1.4, 6.4)
plt.ylim(-0.6, 5.8)
plt.show()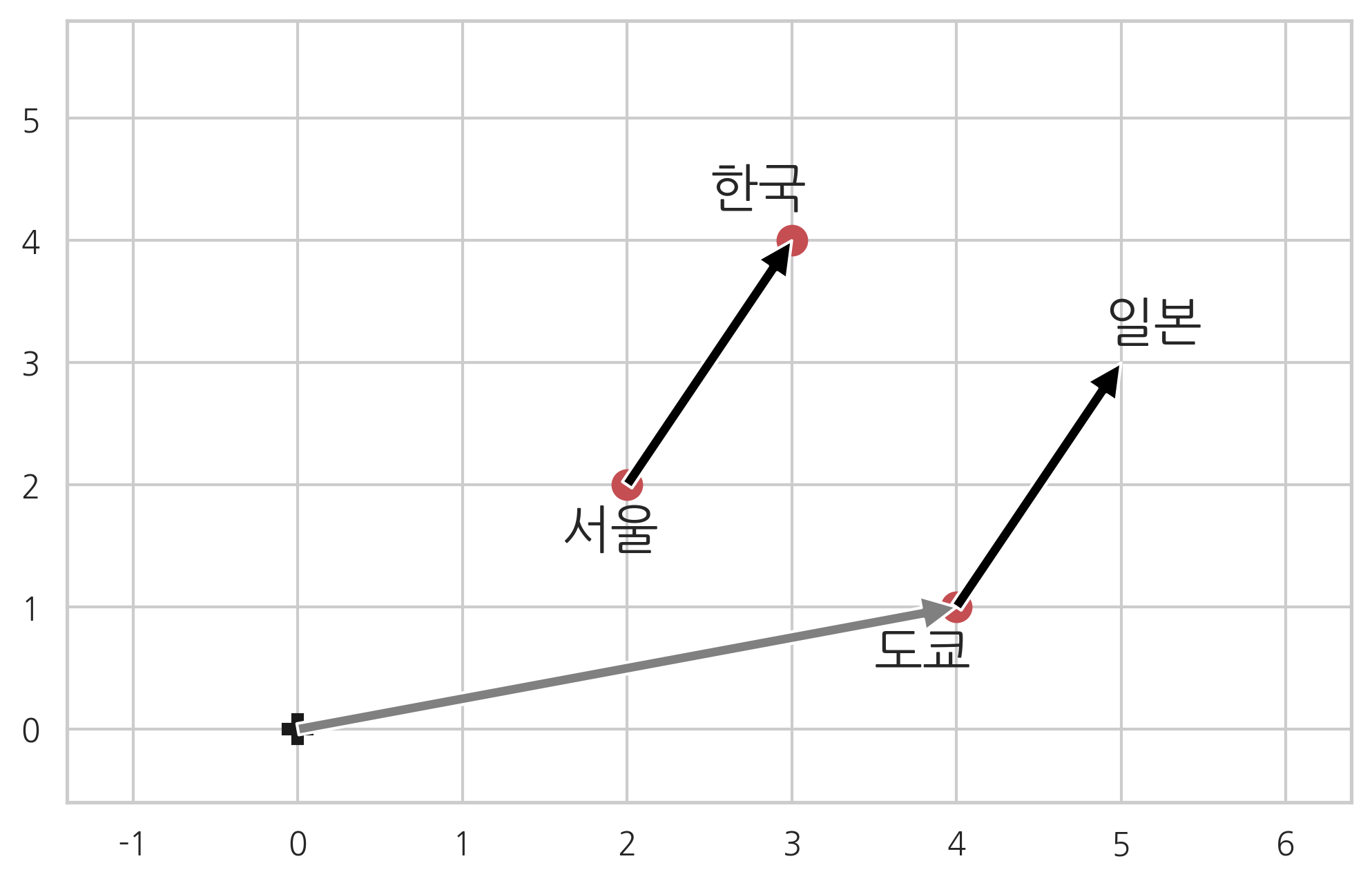

연습 문제 3.1.2

남자배우, 여자배우, 남자, 여자, 이렇게 4가지 단어에 대응하는 4개의 벡터에 대해 위와 같은 관계가 성립한다고 가정하자. 다음 식을 완성하라.

남자배우 = 여자배우 + ?

✒️
배우라는 새로운 단어에 대응하는 벡터를 생각해보면
배우 = 남자배우 - 남자 = 여자배우 - 여자 라 할 수 있고 각 변에 남자를 더하면
남자배우 = 여자배우 - 여자 + 남자

위에서 살펴본 일본=도쿄+(한국−서울)\text{일본} = \text{도쿄} + (\text{한국} - \text{서울})의 예시도 비슷하다.
(국가에서 수도를 빼는 것에 대응하는 벡터) = 일본 - 도쿄 = 한국 - 서울 에서 일본 벡터에 대해 정리하면 같은 결과가 얻어진다.

유클리드 거리

두 벡터가 가리키는 점 사이의 거리를 유클리드 거리(Euclidean distance) 라고 한다. 두 벡터의 유클리드 거리는 벡터의 차의 길이로 구할 수 있다.

벡터의 놈의 정의와 벡터의 차의 정의에서 유클리드 거리는 다음처럼 구한다.

∥a−b∥=∑i=1(ai−bi)2=∑i=1(ai2−2aibi+bi2)=∑i=1ai2+∑i=1bi2−2∑i=1aibi=∥a∥2+∥b∥2−2aTb(3.1.13)\begin{aligned} \| a - b \| &= \sqrt{\sum_{i=1} (a_i - b_i)^2} \\ &= \sqrt{\sum_{i=1} ( a_i^2 - 2 a_i b_i + b_i^2 )} \\ &= \sqrt{\sum_{i=1} a_i^2 + \sum_{i=1} b_i^2 - 2 \sum_{i=1} a_i b_i} \\ &= \sqrt{\| a \|^2 + \| b \|^2 - 2 a^Tb } \end{aligned} \tag{3.1.13}

즉,

∥a−b∥2=∥a∥2+∥b∥2−2aTb(3.1.14)\| a - b \|^2 = \| a \|^2 + \| b \|^2 - 2 a^T b \tag{3.1.14}

벡터의 내적과 삼각함수

두 벡터의 내적은 다음처럼 벡터의 길이 ∥a∥\|a\|, ∥b∥\|b\| 와 두 벡터 사이의 각도 θ\theta의 코사인 함수값으로 계산할 수도 있다.

aTb=∥a∥∥b∥cos⁡θ(3.1.15)a^Tb = \|a\|\|b\| \cos\theta \tag{3.1.15}

여기에서 cos⁡θ\cos\theta는 코사인(cosine) 이라고 하는 함수이다. 코사인은 사인(sine)이라고 하는 함수와 함께 정의할 수 있다. 사인과 코사인을 합쳐서 삼각함수라고 한다.

사인 sin⁡θ\sin\theta의 값은 θ\theta라는 각을 가지는 직각 삼각형에서 빗변(hypotenuse)과 높이(opposite)의 비율을 뜻한다.

코사인 cos⁡θ\cos\theta의 값은 θ\theta라는 각을 가지는 직각 삼각형에서 빗변(hypotenuse)과 밑변(adjacent)의 비율을 뜻한다.

sin⁡θ=ah(3.1.16)\sin\theta = \dfrac{a}{h} \tag{3.1.16}
cos⁡θ=bh(3.1.17)\cos\theta = \dfrac{b}{h} \tag{3.1.17}
plt.plot([0, 1], [0, 2], 'k-', lw=3)
plt.plot([0, 1], [0, 0], 'k-', lw=3)
plt.plot([1, 1], [0, 2], 'k-', lw=3)
plt.text(0.05, 1, "빗변 h")
plt.text(0.35, -0.2, "밑변 b")
plt.text(1.05, 1, "높이 a")
plt.text(0.12, 0.06, r"$\theta$")
plt.xticks(np.arange(-2, 4))
plt.yticks(np.arange(-1, 4))
plt.xlim(-1.1, 2.1)
plt.ylim(-0.5, 2.3)
plt.show()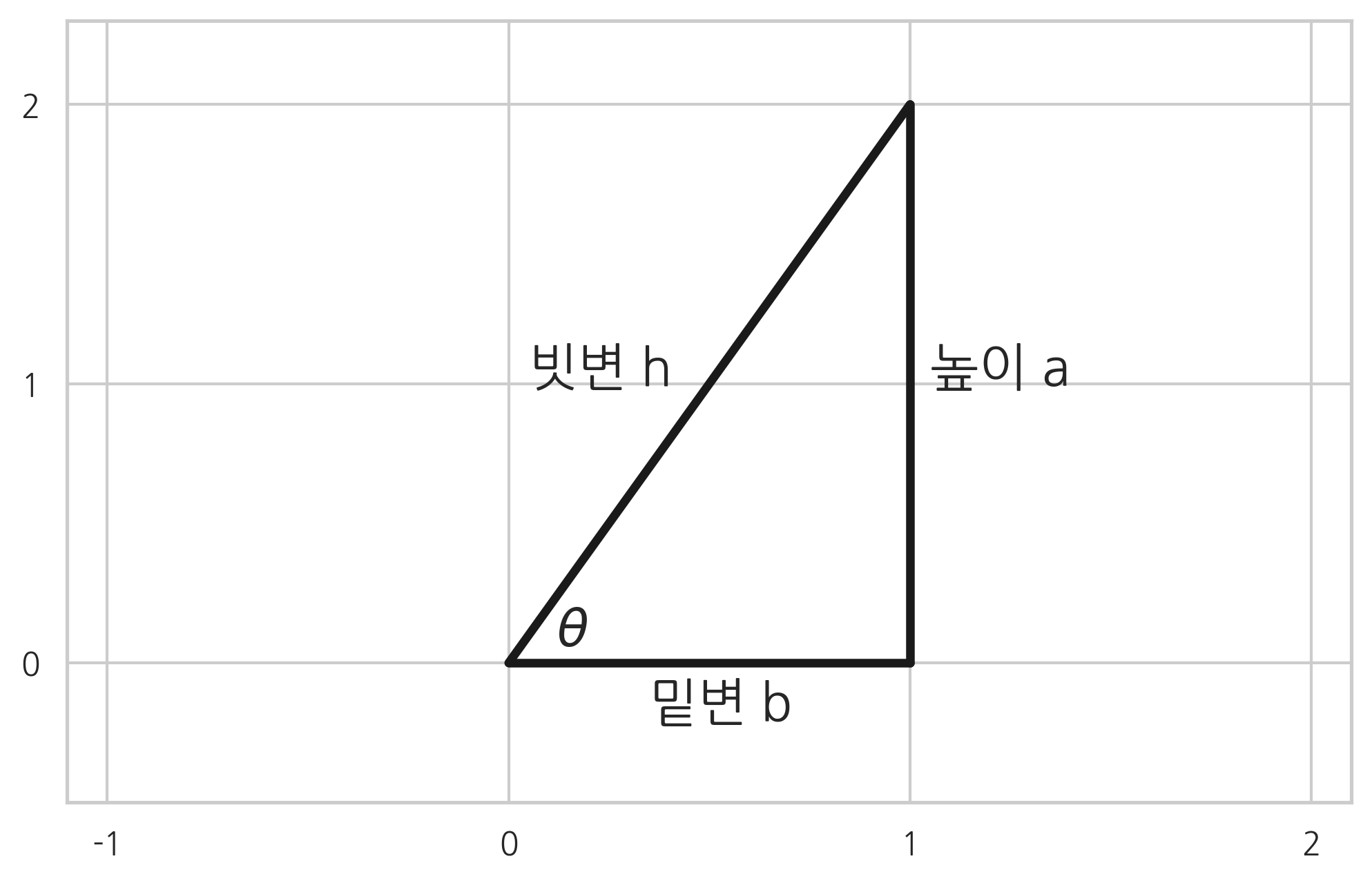

sin⁡θ\sin\theta의 값은 θ\theta가 0에 가까워질수록 0에 가까워지고 θ\theta가 90∘90{}^{\circ}에 가까워질수록 1에 가까워진다.

sin⁡0∘=0(3.1.18)\sin 0^{\circ} = 0 \tag{3.1.18}
sin⁡90∘=1(3.1.19)\sin 90^{\circ} = 1 \tag{3.1.19}

반대로 cos⁡θ\cos\theta의 값은 θ\theta가 0에 가까워질수록 1에 가까워지고 θ\theta가 90∘90{}^{\circ}에 가까워질수록 0에 가까워진다.

cos⁡0∘=1(3.1.20)\cos 0^{\circ} = 1 \tag{3.1.20}
cos⁡90∘=0(3.1.21)\cos 90^{\circ} = 0 \tag{3.1.21}

함수의 그래프로 표현하면 다음과 같다.

x = np.linspace(0, np.pi/2, 100)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x, y1, 'r--', lw=3,  label=r"$\sin\theta$")
plt.plot(x, y2, 'b-', lw=3, label=r"$\cos\theta$")
plt.legend()
plt.xticks([0, np.pi/4, np.pi/2], [r'$0^{\circ}$', r'$45^{\circ}$', r'$90^{\circ}$'])
plt.xlabel(r"$\theta$")
plt.title(r"$\sin\theta$와 $\cos\theta$의 그래프")
plt.show()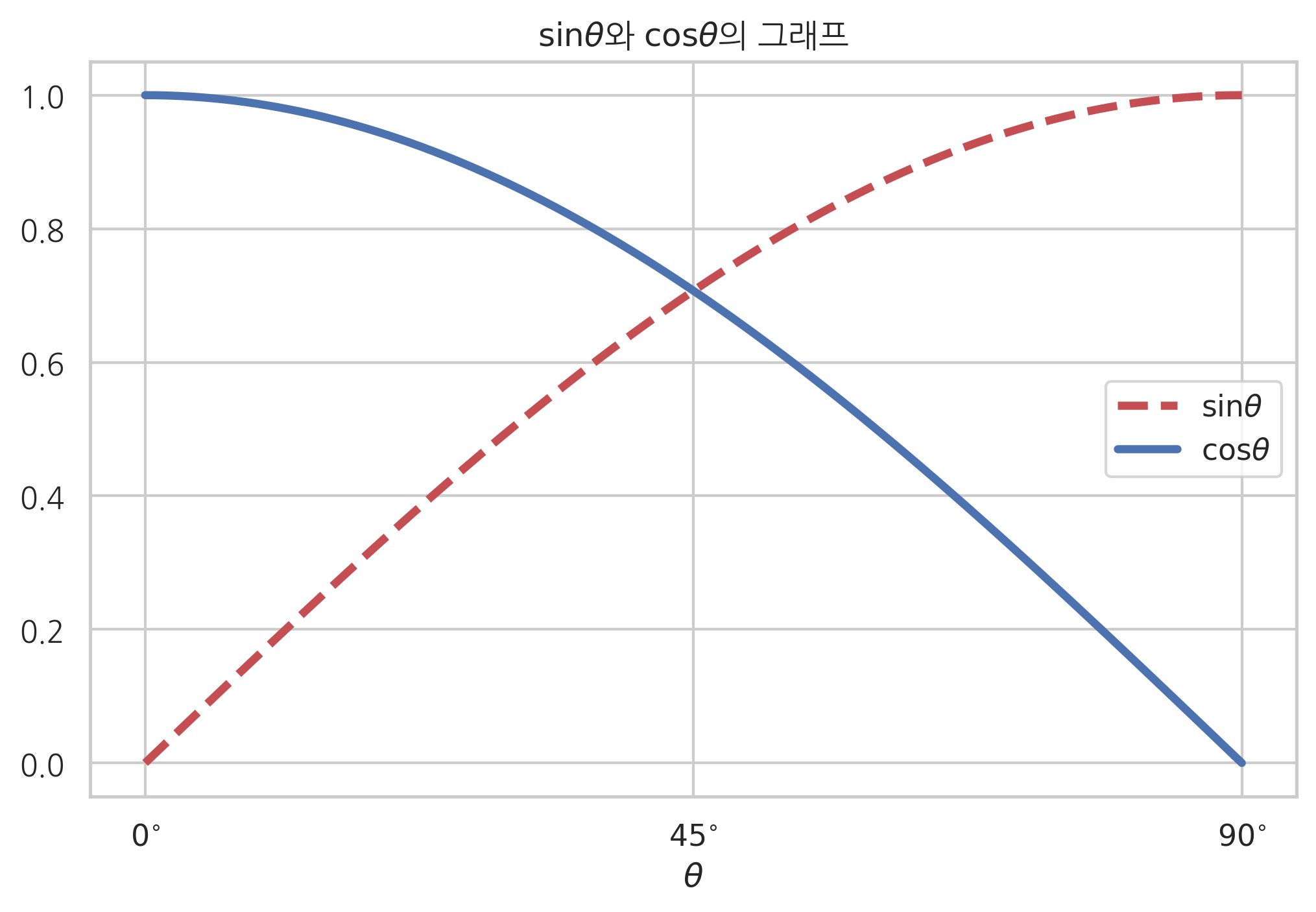

직교

두 벡터 aa와 bb가 이루는 각이 90도이면 서로 직교(orthogonal) 라고 하며 a⊥ba \perp b로 표시한다.

cos⁡90∘=0\cos 90^{\circ} = 0이므로 서로 직교인 두 벡터의 내적은 0이 된다.

aTb=bTa=0        ↔        a⊥b(3.1.22)a^T b = b^T a = 0 \;\;\;\; \leftrightarrow \;\;\;\; a \perp b \tag{3.1.22}

예를 들어 다음 두 벡터는 서로 직교한다.

a=[11],    b=[−11]        →        aTb=[11][−11]=−1+1=0(3.1.23)a = \begin{bmatrix}1 \\ 1\end{bmatrix} ,\;\; b = \begin{bmatrix}-1 \\ 1\end{bmatrix} \;\;\;\; \rightarrow \;\;\;\; a^T b = \begin{bmatrix}1 & 1\end{bmatrix} \begin{bmatrix}-1 \\ 1\end{bmatrix} = -1 + 1 = 0 \tag{3.1.23}
a = np.array([1, 1])
b = np.array([-1, 1])
a @ b
0

연습 문제 3.1.3

(1) 다음 벡터에 대해 직교하는 단위벡터를 찾아라.

x=[10](3.1.24)x = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \tag{3.1.24}

✒️
y = (0, 1), (0,-1)

(2) 다음 벡터에 대해 직교하는 단위벡터를 찾아라.

x=[11](3.1.25)x = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \tag{3.1.25}

y = 121\over\sqrt2(1, -1), 121\over\sqrt2(-1,1)

(3) 다음 두 벡터에 대해 모두 직교하는 단위벡터를 찾아라.

x=[110],    y=[100](3.1.26)x = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, \;\; y = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \tag{3.1.26}

a+b=0a+b=0
a=0a=0
c2=1c^2 = 1
∴\therefore z = (0, 0, 1), (0, 0, -1)

정규직교

만약 NN개의 단위벡터 v1,v2,⋯ ,vNv_1, v_2, \cdots, v_N가 서로 직교하면 정규직교(orthonormal) 라고 한다.

∥vi∥=1    ↔    viTvi=1(3.1.27)\|v_i\| = 1 \;\;\leftrightarrow \;\; v_i^Tv_i = 1 \tag{3.1.27}
viTvj=0    (i≠j)(3.1.28)v_i^T v_j = 0 \;\;(i \neq j) \tag{3.1.28}

연습 문제 3.1.4

직교하는 두 NN차원 벡터 a,ba, b에 대해 다음 식이 성립함을 보여라

∥a+b∥2=∥a∥2+∥b∥2(3.1.29)\| a + b \|^2 = \| a \|^2 + \| b \|^2 \tag{3.1.29}

✒️
좌변=(a+b)T(a+b)=(aT+bT)(a+b)=aTa+aTb+bTa+bTb=(a+b)^T(a+b)=(a^T+b^T)(a+b)=a^Ta+a^Tb+b^Ta+b^Tb
우변=aTa+bTb=a^Ta+b^Tb
a, b 가 서로 직교하므로 두 벡터를 내적한 값은 0이다.
즉 좌변을 전개한 식에서 2, 3번째 항이 0이므로 우변과 같아진다.

N=2N=2일 때 이 식은 피타고라스의 정리가 된다.

연습 문제 3.1.5

정규직교하는 세 개의 3차원 벡터 v1,v2,v3v_1, v_2, v_3로 이루어진 행렬 VV에 대해서 다음 등식이 성립함을 보여라.

V=[v1v2v3](3.1.30)V = \begin{bmatrix} v_1 & v_2 & v_3 \end{bmatrix} \tag{3.1.30}

(1)

VTV=I(3.1.31)V^TV = I \tag{3.1.31}

✒️
정규직교이므로 자기 자신과의 내적은 1, 다른 벡터와의 내적은 0이다.

VTV=[v1Tv1v1Tv2v1Tv3v2Tv1v2Tv2v2Tv3v3Tv1v3Tv2v3Tv3]=[100010001]=IV^TV = \begin{bmatrix} v_1^Tv_1 & v_1^Tv_2 & v_1^Tv_3 \\ v_2^Tv_1 & v_2^Tv_2 & v_2^Tv_3 \\ v_3^Tv_1 & v_3^Tv_2 & v_3^Tv_3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} =I

(2)

V−1=VT(3.1.32)V^{-1} = V^T \tag{3.1.32}

✒️
(3.1.31) 의 양변에 det을 취하면 V의 det 값이 0이 아니므로 역행렬이 존재하고
역행렬의 정의에 의해 (3.1.32)가 얻어진다.

코사인 유사도

두 벡터의 방향이 비슷할수록 벡터가 비슷하다고 간주하여 두 벡터 사이의 각의 코사인값을 코사인 유사도(cosine similarity) 라고 한다. 코사인값은 각도가 0일때 가장 커지므로 두 벡터가 같은 방향을 가리키고 있으면 코사인 유사도가 최댓값 1을 가진다.

cosine similarity=cos⁡θ=xTy∥x∥∥y∥(3.1.33)\text{cosine similarity} = \cos\theta = \dfrac{x^Ty}{\|x\|\|y\|} \tag{3.1.33}

코사인 유사도는 나중에 공부할 추천시스템(recommender system)에서 사용자의 취향이 얼마나 비슷한지를 계산할 때 사용된다. 코사인 유사도를 이용하면 다음처럼 코사인 거리(cosine distance) 도 정의할 수 있다.

cosine distance=1−cosine similarity=1−xTy∥x∥∥y∥(3.1.34)\text{cosine distance} = 1 - \text{cosine similarity} = 1 - \dfrac{x^Ty}{\|x\|\|y\|} \tag{3.1.34}

연습 문제 3.1.6

a, b, c, 3명의 사용자가 4개의 영화에 준 평점을 다음처럼 벡터로 표현하였다.

a=[4522],    b=[4020],    c=[2201](3.1.35)a = \begin{bmatrix} 4 \\ 5 \\ 2 \\ 2 \end{bmatrix}, \;\; b = \begin{bmatrix} 4 \\ 0 \\ 2 \\ 0 \end{bmatrix}, \;\; c = \begin{bmatrix} 2 \\ 2 \\ 0 \\ 1 \end{bmatrix} \tag{3.1.35}

(1) a, b, c 사이의 유클리드 거리를 구하라. 어느 두 사용자가 가장 가까운가? 또 어느 두 사용자가 가장 멀리 떨어져 있는가?
(2) a, b, c 사이의 코사인 거리를 구하라. 어느 두 사용자가 가장 가까운가? 또 어느 두 사용자가 가장 멀리 떨어져 있는가?
✒️

∥a−b∥=∑i=1(ai−bi)2=∑i=1(ai2−2aibi+bi2)=∑i=1ai2+∑i=1bi2−2∑i=1aibi=∥a∥2+∥b∥2−2aTb(3.1.13)\begin{aligned} \| a - b \| &= \sqrt{\sum_{i=1} (a_i - b_i)^2} \\ &= \sqrt{\sum_{i=1} ( a_i^2 - 2 a_i b_i + b_i^2 )} \\ &= \sqrt{\sum_{i=1} a_i^2 + \sum_{i=1} b_i^2 - 2 \sum_{i=1} a_i b_i} \\ &= \sqrt{\| a \|^2 + \| b \|^2 - 2 a^Tb } \end{aligned} \tag{3.1.13}
cosine distance=1−cosine similarity=1−xTy∥x∥∥y∥(3.1.34)\text{cosine distance} = 1 - \text{cosine similarity} = 1 - \dfrac{x^Ty}{\|x\|\|y\|} \tag{3.1.34}

import numpy as np
a = np.array([4, 5, 2, 2])
b = np.array([4, 0, 2, 0])
c = np.array([2, 2, 0, 1])
def u_dist(x, y):
    return np.linalg.norm(x - y)
def cos_dist(x, y):
    return 1 - (x @ y) / (np.linalg.norm(x) * np.linalg.norm(y))
print("{}와 {} 사이의 유클리드 거리:{}".format('a', 'b', u_dist(a, b)))
print("{}와 {} 사이의 유클리드 거리:{}".format('a', 'c', u_dist(a, c)))
print("{}와 {} 사이의 유클리드 거리:{}".format('b', 'c', u_dist(b, c)))
print("{}와 {} 사이의 코사인 거리:{}".format('a', 'b', cos_dist(a, b)))
print("{}와 {} 사이의 코사인 거리:{}".format('a', 'c', cos_dist(a, c)))
print("{}와 {} 사이의 코사인 거리:{}".format('b', 'c', cos_dist(b, c)))
a와 b 사이의 유클리드 거리:5.385164807134504 
a와 c 사이의 유클리드 거리:4.242640687119285 
b와 c 사이의 유클리드 거리:3.605551275463989 
a와 b 사이의 코사인 거리:0.36112343500006017 
a와 c 사이의 코사인 거리:0.04761904761904767 
b와 c 사이의 코사인 거리:0.40371520600005606

유클리드 거리: b, c가 가장 가깝다. a, b가 가장 멀다.
코사인 거리: a, c가 가장 가깝다. b, c가 가장 멀다.

벡터의 분해와 성분

어떤 두 벡터 aa, bb의 합이 다른 벡터 cc가 될 때 cc가 두 벡터 성분(component) aa, bb으로 분해(decomposition) 된다고 말한다.

연습 문제 3.1.7

다음 벡터를 두 개의 벡터로 분해하는 방법을 두 가지 이상 찾고 평면 위에 각각 화살표로 표기하라.

x=[10](3.1.36)x = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \tag{3.1.36}

✒️
x = (1, 0) = (1, 1) + (0, -1) # red line
x = (1, 0) = (1, -1) + (0, 1) # blue line

import matplotlib.pylab as plt
plt.arrow(0,0,1,0, head_width=0.05, head_length=0.1)
plt.arrow(0,0,1,1, head_width=0.05, head_length=0.1, color='r')
plt.arrow(1,1,0,-1, head_width=0.05, head_length=0.1, color='r')
plt.arrow(0,0,1,-1, head_width=0.05, head_length=0.1, color='b')
plt.arrow(1,-1,0,1, head_width=0.05, head_length=0.1, color='b')
plt.show()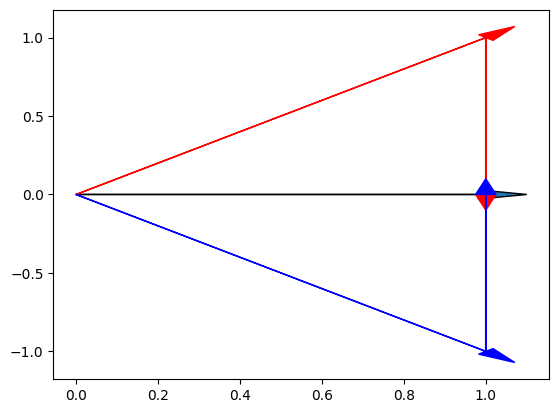

투영성분과 직교성분

벡터 aa를 다른 벡터 bb에 직교하는 성분과 벡터 bb에 평행한 성분으로로 분해할 수 있는데, 평행한 성분을 벡터 bb에 대한 투영성분(projection), 벡터 bb에 직교하는 성분을 벡터 bb에 대한 직교성분(rejection) 이라고 하며 각각 다음과 같이 표기한다.

a∥b(3.1.37)a^{\Vert b} \tag{3.1.37}
a⊥b(3.1.38)a^{\perp b} \tag{3.1.38}

투영성분의 길이는 다음처럼 구할 수 있다.

∥a∥b∥=∥a∥cos⁡θ=∥a∥∥b∥cos⁡θ∥b∥=aTb∥b∥=bTa∥b∥=aTb∥b∥(3.1.39)\| a^{\Vert b} \| = \|a\|\cos\theta = \dfrac{\|a\|\|b\|\cos\theta}{\|b\|} = \dfrac{a^Tb}{\|b\|} = \dfrac{b^Ta}{\|b\|} = a^T\dfrac{b}{\|b\|} \tag{3.1.39}

만약 벡터 bb 자체가 이미 단위벡터이면 단위벡터에 대한 투영길이는 내적이 된다.

∥a∥b∥=aTb(3.1.40)\| a^{\Vert b} \| = a^Tb \tag{3.1.40}

투영성분 성분 벡터는 투영성분 길이와 벡터 bb 방향의 단위벡터의 곱이다.

a∥b=aTb∥b∥b∥b∥=aTb∥b∥2b(3.1.41)a^{\Vert b} = \dfrac{a^Tb}{\|b\|} \dfrac{b}{\|b\|}= \dfrac{a^Tb}{\|b\|^2}b \tag{3.1.41}

직교성분 벡터는 원래의 벡터에서 투영성분 성분 벡터를 뺀 나머지다.

a⊥b=a−a∥b(3.1.42)a^{\perp b} = a - a^{\Vert b} \tag{3.1.42}
a = np.array([1, 2])
b = np.array([2, 0])
a2 = (a @ b) / np.linalg.norm(b) * np.array([1, 0])
a1 = a - a2
plt.annotate('', xy=b, xytext=(0, 0), arrowprops=green)
plt.annotate('', xy=a2, xytext=(0, 0), arrowprops=blue)
plt.annotate('', xy=a1, xytext=(0, 0), arrowprops=blue)
plt.annotate('', xy=a, xytext=(0, 0), arrowprops=red)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(a[0], a[1], 'ro', ms=10)
plt.plot(b[0], b[1], 'ro', ms=10)
plt.text(0.35, 1.15, "$a$")
plt.text(1.55, 0.15, "$b$")
plt.text(-0.5, 1.05, "$a^{\perp b}$")
plt.text(0.50, 0.15, "$a^{\Vert b}$")
plt.xticks(np.arange(-10, 10))
plt.yticks(np.arange(-10, 10))
plt.xlim(-1.2, 4.1)
plt.ylim(-0.5, 3.2)
plt.show()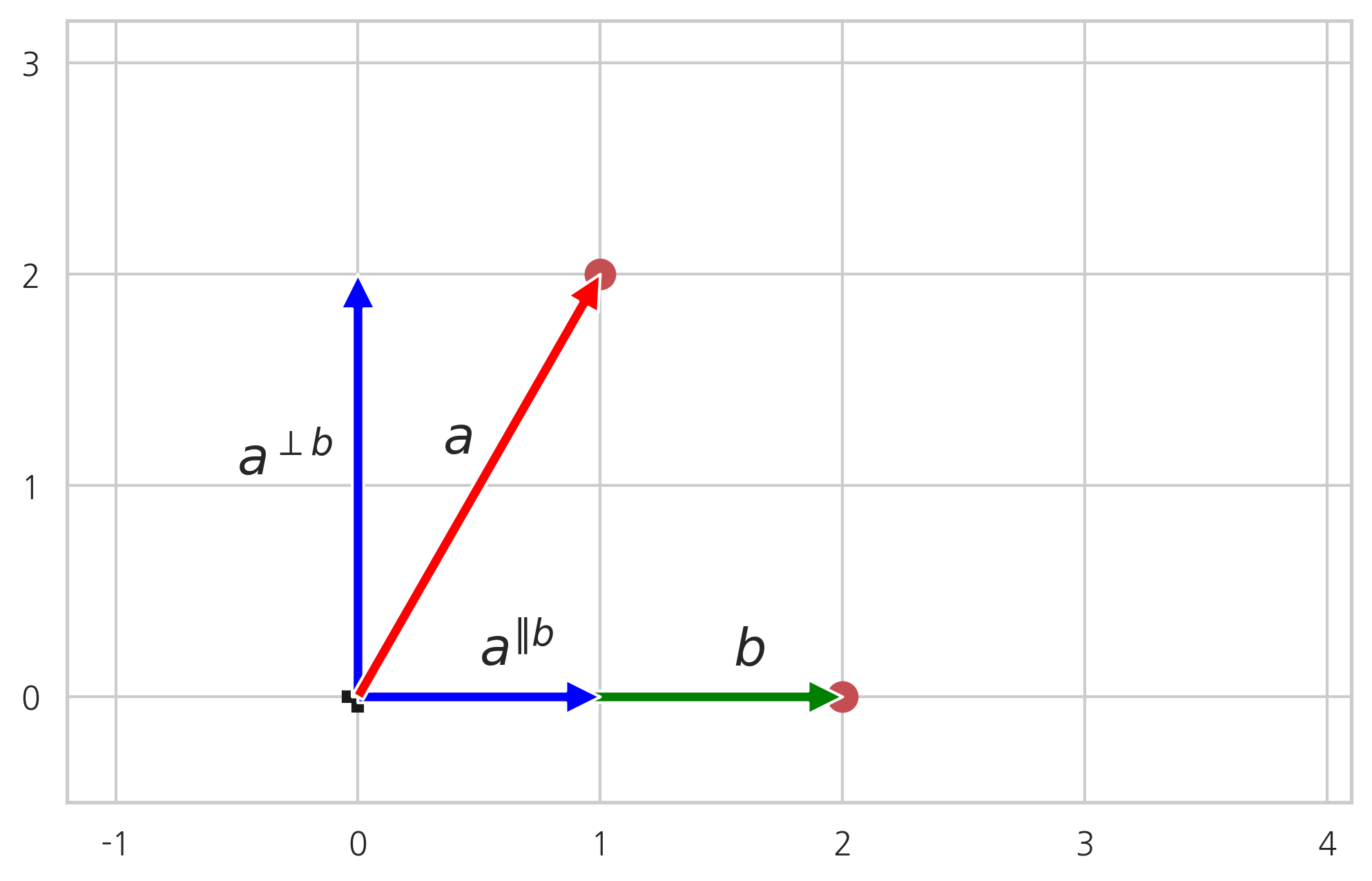

연습 문제 3.1.8

a=[12],    b=[20](3.1.43)a=\begin{bmatrix}1 \\ 2\end{bmatrix}, \;\; b=\begin{bmatrix}2 \\ 0\end{bmatrix} \tag{3.1.43}

일 때, 투영성분 a∥ba^{\Vert b}, 직교성분 a⊥ba^{\perp b}를 구하라.
✒️

a∥b=aTb∥b∥b∥b∥=aTb∥b∥2b(3.1.41)a^{\Vert b} = \dfrac{a^Tb}{\|b\|} \dfrac{b}{\|b\|}= \dfrac{a^Tb}{\|b\|^2}b \tag{3.1.41}
import numpy as np
def decomp(x, y):
    projection = ((x @ y) / (np.linalg.norm(y))**2) * y
    rejection = x - projection
    return projection, rejection
a = np.array([1,2])
b = np.array([2,0])
decomp(a, b)
(array([1., 0.]), array([0., 2.]))

연습 문제 3.1.9

만약 vv가 원점을 지나는 직선의 방향을 나타내는 단위벡터라고 하자. 이때 그 직선 위에 있지 않는 어떤 점 xx와 그 직선과의 거리의 제곱이 다음과 같음을 증명하라.

∥x∥2−(xTv)2(3.1.44)\| x \|^2 - (x^Tv)^2 \tag{3.1.44}

✒️
xx를 vv와 평행한 성분x∥vx^{\Vert v}과 수직인 성분x⊥vx^{\perp v}으로 분해하면 직선과의 거리의 제곱은 x⊥vx^{\perp v}의 크기의 제곱과 같다. vv는 단위벡터이므로 ∥v∥2=1\|v\|^2=1이므로

x∥v=xTv∥v∥2v=(xTv)vx^{\Vert v} = \dfrac{x^Tv}{\|v\|^2}v=(x^Tv)v 이고 ∥x⊥v∥2=∥x−(xTv)v∥2=(x−(xTv)v)T(x−(xTv)v)\|x^{\perp v}\|^2 = \|x-(x^Tv)v\|^2=(x-(x^Tv)v)^T(x-(x^Tv)v)
=(xT−(xTv)vT)(x−(xTv)v)=∥x∥2−(xTv)2=(x^T-(x^Tv)v^T)(x-(x^Tv)v)=\| x \|^2 - (x^Tv)^2

v = np.array([2, 1]) / np.sqrt(5)
x = np.array([1, 3])
plt.plot(0, 0, 'kP', ms=10)
plt.annotate('', xy=v, xytext=(0, 0), arrowprops=black)
plt.plot([-2, 8], [-1, 4], 'b--', lw=2)
plt.plot([1, 2], [3, 1], 'g:', lw=2)
plt.plot(x[0], x[1], 'ro', ms=10)
plt.text(0.1, 0.5, "$v$")
plt.text(0.6, 3.2, "$x$")
plt.xticks(np.arange(-3, 15))
plt.yticks(np.arange(-1, 5))
plt.xlim(-3, 7)
plt.ylim(-1, 5)
plt.show()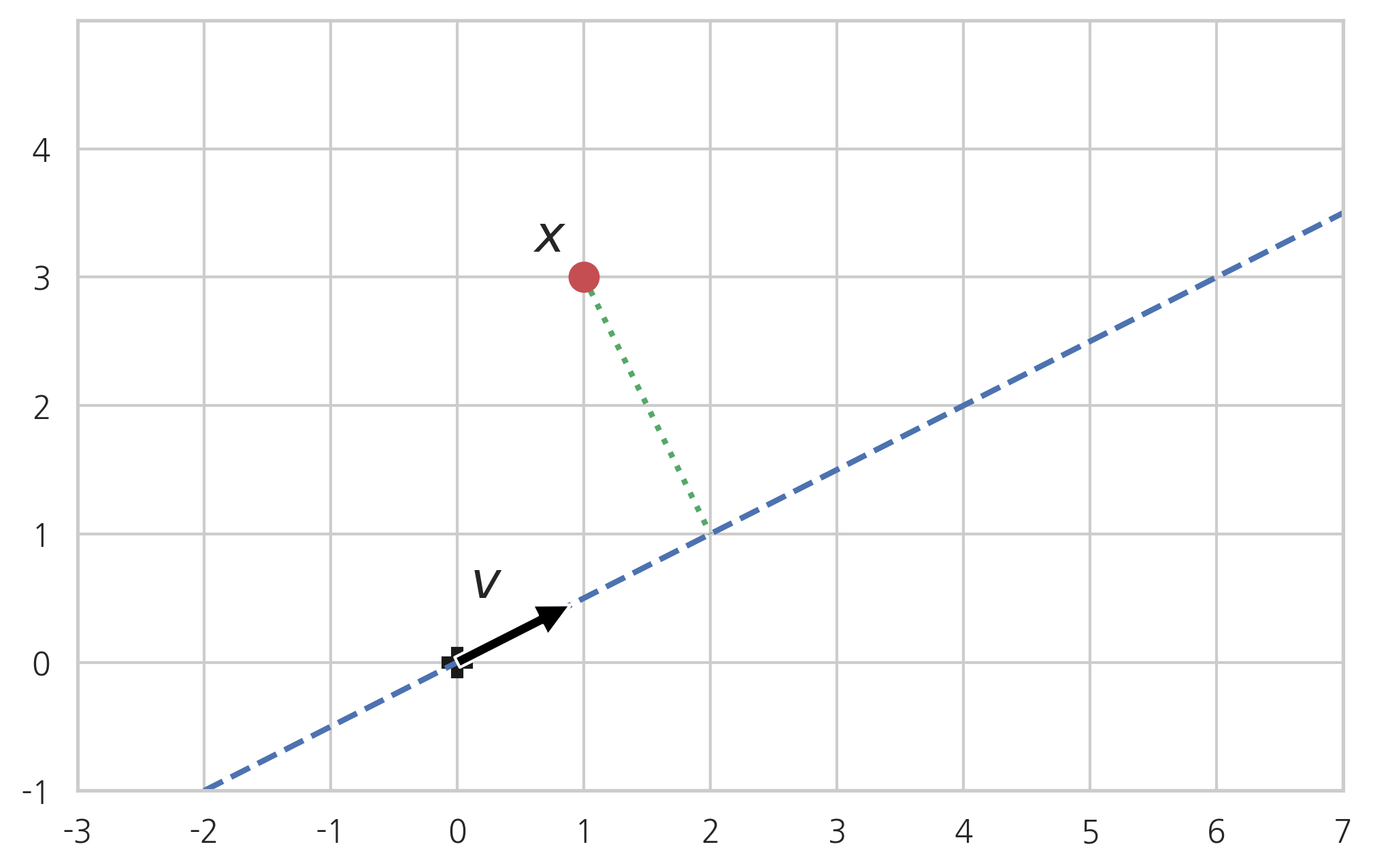

직선의 방정식

어떤 벡터 ww가 있을 때

  • 원점에서 출발한 벡터 ww가 가리키는 점을 지나면서

  • 벡터 ww에 수직인

직선의 방정식을 구해보자.

위 두 조건을 만족하는 직선 상의 임의의 점을 가리키는 벡터를 xx라고 하면, 벡터 xx가 가리키는 점과 벡터 ww가 가리키는 점을 이은 벡터 x−wx - w는 조건에 따라 벡터 ww와 직교해야 한다. 따라서 다음 식이 성립한다.

wT(x−w)=0(3.1.45)w^T(x - w) = 0 \tag{3.1.45}

정리하면 다음과 같아진다.

wT(x−w)=wTx−wTw=wTx−∥w∥2(3.1.46)w^T(x - w) = w^Tx - w^Tw = w^Tx - \| w \|^2 \tag{3.1.46}
wTx−∥w∥2=0(3.1.47)w^Tx - \| w \|^2 = 0 \tag{3.1.47}

이 직선과 원점 사이의 거리는 벡터 ww의 놈 ∥w∥\|w\|이다.

∥w∥(3.1.48)\|w\| \tag{3.1.48}
w = np.array([1, 2])
x1 = np.array([3, 1])
x2 = np.array([-1, 3])
plt.annotate('', xy=w, xytext=(0, 0), arrowprops=black)
plt.annotate('', xy=x1, xytext=(0, 0), arrowprops=green)
plt.annotate('', xy=x2, xytext=(0, 0), arrowprops=green)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(w[0], w[1], 'ro', ms=10)
plt.plot(x1[0], x1[1], 'ro', ms=10)
plt.plot(x2[0], x2[1], 'ro', ms=10)
plt.plot([-3, 5], [4, 0], 'r-', lw=5)
plt.text(-0.2, 1.5, "벡터 $w$")
plt.text(1.55, 0.25, "$x_1$")
plt.text(-0.9, 1.40, "$x_2$")
plt.text(1.8, 1.8, "$x_1 - w$")
plt.text(-0.2, 2.8, "$x_2 - w$")
plt.text(3.6, 0.8, "직선 $x$")
plt.xticks(np.arange(-2, 5))
plt.yticks(np.arange(-1, 5))
plt.xlim(-2, 5)
plt.ylim(-0.6, 3.6)
plt.show()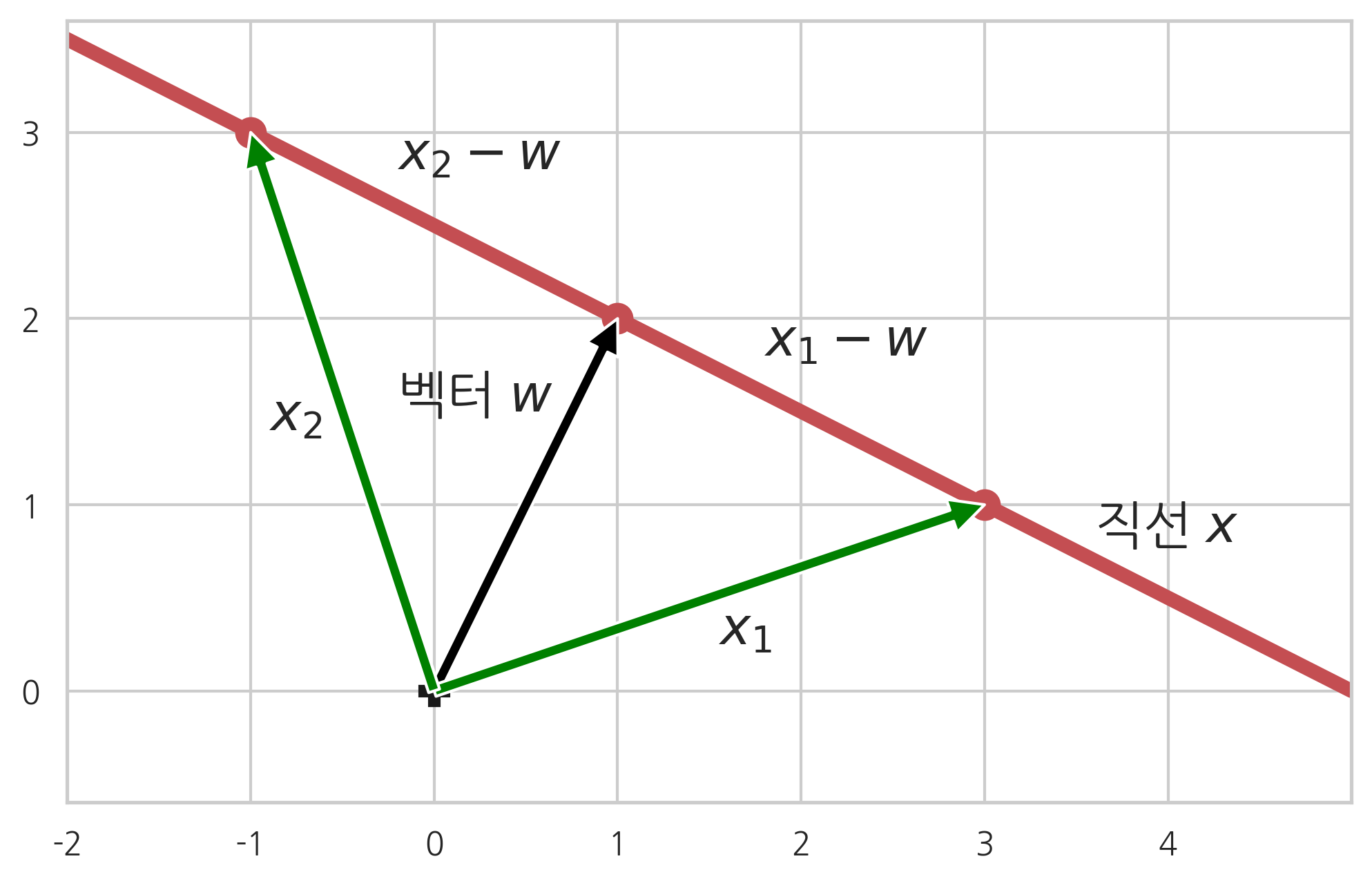

예를 들어

w=[12](3.1.49)w = \begin{bmatrix}1 \\ 2\end{bmatrix} \tag{3.1.49}

일 때

∥w∥2=5(3.1.50)\| w \|^2 = 5 \tag{3.1.50}
[12][x1x2]−5=x1+2x2−5=0(3.1.51)\begin{bmatrix}1 & 2\end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \end{bmatrix} - 5 = x_1 + 2x_2 - 5 = 0 \tag{3.1.51}
x1+2x2=5(3.1.52)x_1 + 2x_2 = 5 \tag{3.1.52}

이 방정식은 벡터 ww가 가리키는 점 (1,2)(1, 2)를 지나면서 벡터 ww에 수직인 직선을 뜻한다. 이 직선과 원점 사이의 거리는 ∥w∥=5\|w\|=\sqrt{5}이다.

이번에는 벡터 ww가 가리키는 점을 지나야 한다는 조건을 없애고 단순히

  • 벡터 ww에 수직인

직선 xx의 방정식을 구해보자.

이때는 직선이 ww가 아니라 ww와 방향이 같고 길이가 다른 벡터 w′=cww'=cw을 지날 것이다. cc는 양의 실수이다.

위에서 했던 방법으로 다시 직선의 방정식을 구하면 다음과 같다.

w′Tx−∥w′∥2=cwTx−c2∥w∥2=0(3.1.53)w'^Tx - \| w' \|^2 = cw^Tx - c^2 \| w \|^2 = 0 \tag{3.1.53}
wTx−c∥w∥2=0(3.1.54)w^Tx - c \| w \|^2 = 0 \tag{3.1.54}

여기에서 c∥w∥2c \| w \|^2는 임의의 수가 될 수 있으므로 단순히 벡터 ww에 수직인 직선의 방정식은 다음과 같이 나타낼 수 있다.

wTx−w0=0(3.1.55)w^Tx - w_0 = 0 \tag{3.1.55}

이 직선과 원점 사이의 거리는 다음과 같다.

c∥w∥=w0∥w∥(3.1.56)c \| w \| = \dfrac{w_0}{\|w\|} \tag{3.1.56}
w = np.array([1, 2])
plt.annotate('', xy=w, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=0.5 * w, xytext=(0, 0), arrowprops=black)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(0.5 * w[0], 0.5 * w[1], 'ro', ms=10)
plt.plot([-2, 5], [2.25, -1.25], 'r-', lw=5)
plt.text(-0.7, 0.8, "벡터 $cw$")
plt.text(-0.1, 1.6, "벡터 $w$")
plt.text(1, 1, "직선 $x$")
plt.xticks(np.arange(-2, 5))
plt.yticks(np.arange(-1, 5))
plt.xlim(-2, 5)
plt.ylim(-0.6, 3.6)
plt.show()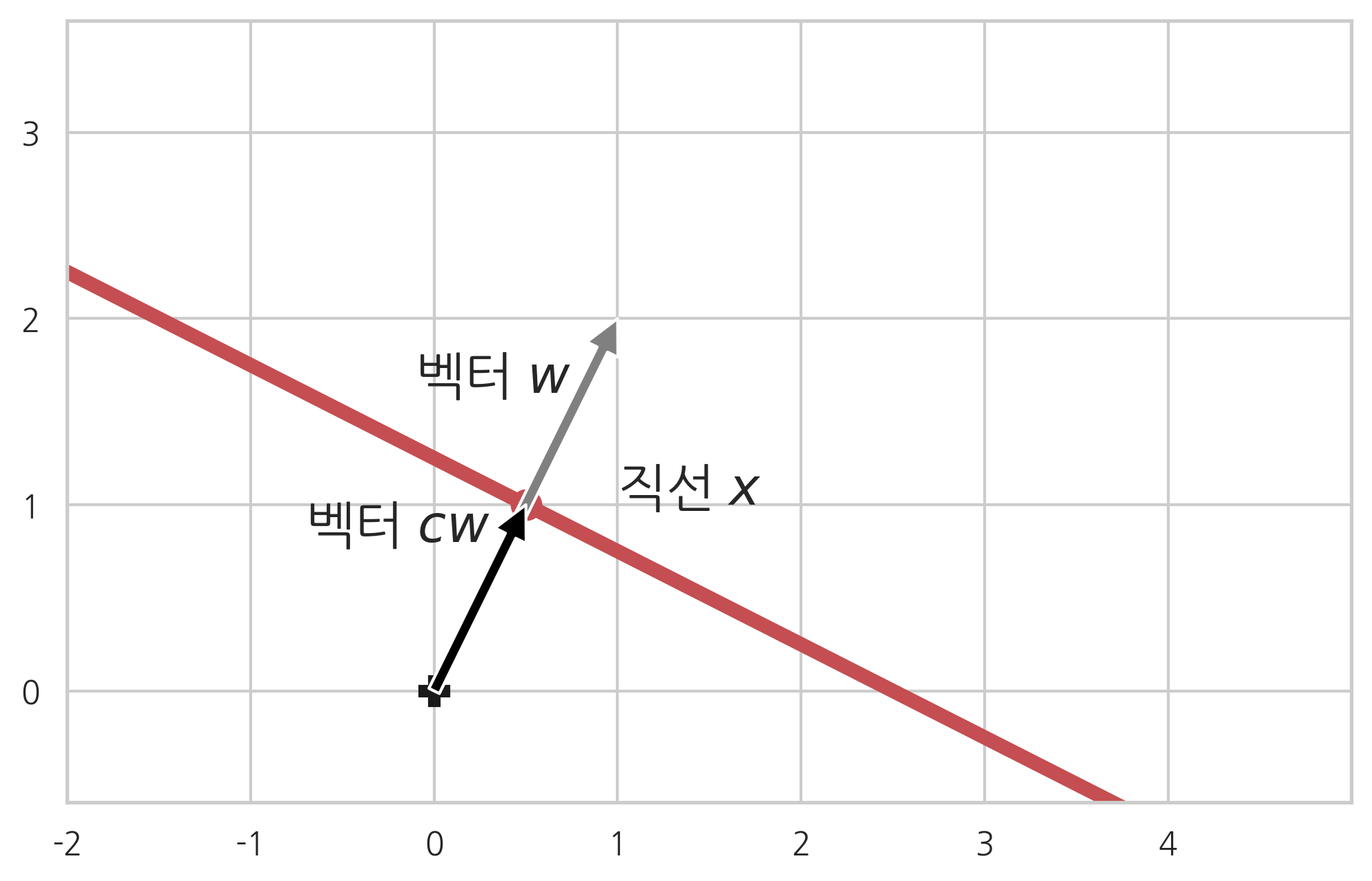

예를 들어 c=0.5c=0.5이면 벡터 w=[1,2]Tw=[1, 2]^T에 수직이고 원점으로부터의 거리가 52\frac{\sqrt{5}}{2}인 직선이 된다.

x1+2x2−2.5=0(3.1.57)x_1 + 2x_2 - 2.5 = 0 \tag{3.1.57}

연습 문제 3.1.10

직선 wTx−w0=0w^Tx - w_0 = 0과 원점 사이의 거리가 다음과 같다는 것을 증명하라.

w0∥w∥(3.1.58)\dfrac{w_0}{\|w\|} \tag{3.1.58}

✒️
주어진 직선에서 w0=c∥w∥2w_0=c\|w\|^2 라 하면 wTx−c∥w∥2=wT(x−cw)=0w^Tx - c\|w\|^2 = w^T(x-cw)=0 이므로
해당 직선은 cwcw가 가르키는 점을 지나며 w에 수직인 직선을 의미하고
이 때 원점에서 직선까지의 거리는 c∥w∥=w0∥w∥c\|w\|=\dfrac{w_0}{\|w\|}이다.

직선과 점의 거리

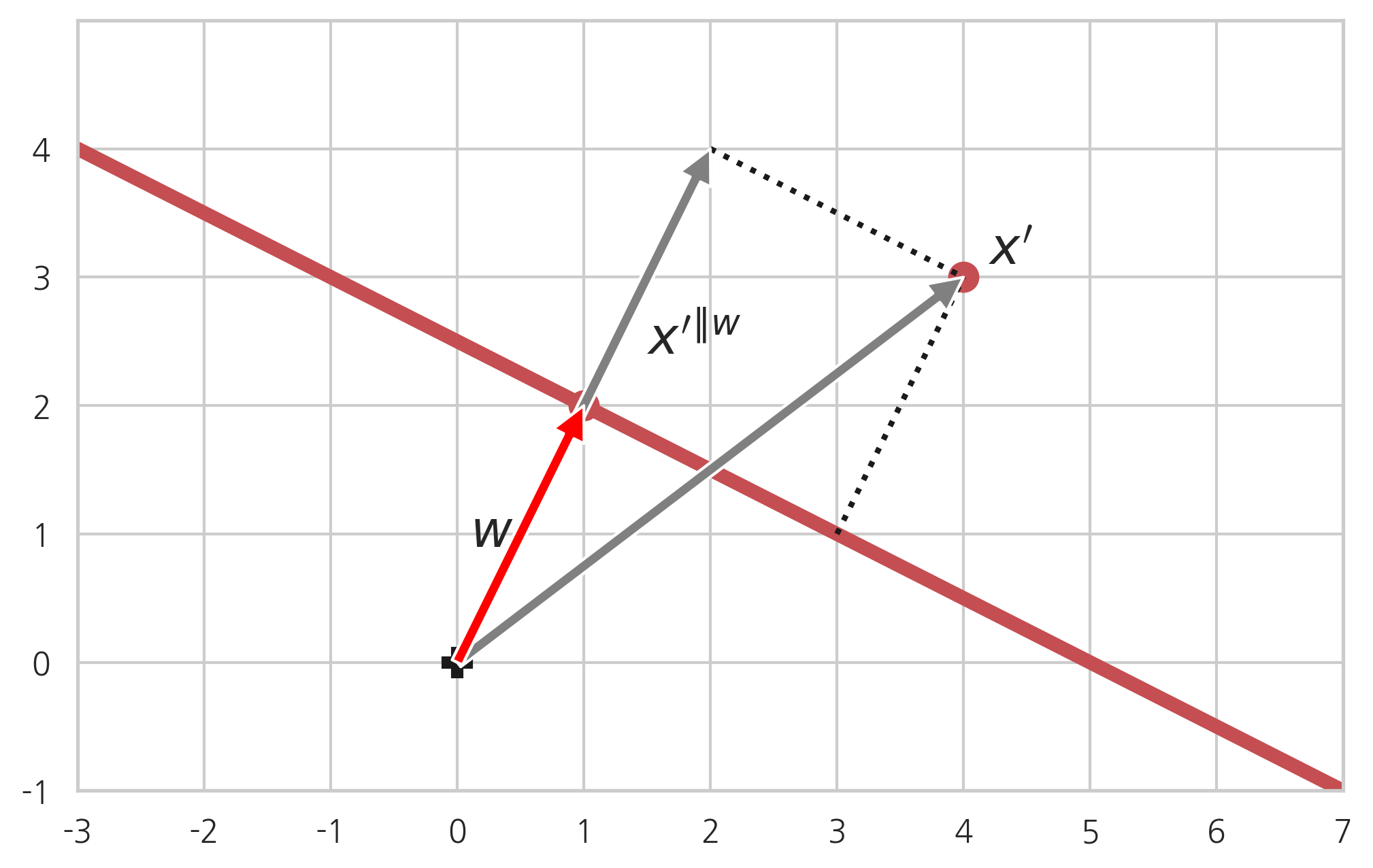
이번에는 직선 wTx−∥w∥2=0w^Tx - \|w\|^2 = 0 과 이 직선 위에 있지 않은 점 x′x' 사이의 거리를 구해보자.

벡터 ww에 대한 벡터 x′x'의 투영성분 x′∥wx'^{\Vert w}의 길이는 다음과 같다.

∥x′∥w∥=wTx′∥w∥(3.1.59)\|x'^{\Vert w}\| = \dfrac{w^Tx'}{\|w\|} \tag{3.1.59}

직선과 점 x′x' 사이의 거리는 이 길이에서 원점에서 직선까지의 거리 ∥w∥\|w\|를 뺀 값의 절댓값이다.

∣∥x′∥w∥−∥w∥∣=∣wTx′∥w∥−∥w∥∣=∣wTx′−∥w∥2∣∥w∥(3.1.60)\left| \|x'^{\Vert w}\| - \|w\| \right| = \left| \dfrac{w^Tx'}{\|w\|} - \|w\| \right| = \dfrac{\left|w^Tx' - \|w\|^2 \right|}{\|w\|} \tag{3.1.60}

직선의 방정식이 wTx−w0=0w^Tx - w_0 = 0이면 직선과 점의 거리는 다음과 같다.

∣wTx′−w0∣∥w∥(3.1.61)\dfrac{\left|w^Tx' - w_0 \right|}{\|w\|} \tag{3.1.61}

이 공식은 나중에 분류 방법의 하나인 서포트 벡터 머신(SVM: Support Vector Machine)에서 사용된다.

연습 문제 3.1.11

직선의 방정식이 wTx−w0=0w^Tx - w_0 = 0이면 직선과 점의 거리는 다음과 같다는 것을 증명하라.

∣wTx′−w0∣∥w∥(3.1.62)\dfrac{\left|w^Tx' - w_0 \right|}{\|w\|} \tag{3.1.62}

✒️

w = np.array([1, 2])
x1 = np.array([4, 3])
x2 = np.array([1, 2]) * 2
plt.annotate('', xy=x1, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=x2, xytext=(0, 0), arrowprops=gray)
plt.annotate('', xy=w, xytext=(0, 0), arrowprops=red)
plt.plot(0, 0, 'kP', ms=10)
plt.plot(w[0], w[1], 'ro', ms=10)
plt.plot(x1[0], x1[1], 'ro', ms=10)
plt.plot([-3, 7], [4, -1], 'r-', lw=5)
plt.plot([2, 4], [4, 3], 'k:', lw=2)
plt.plot([3, 4], [1, 3], 'k:', lw=2)
plt.text(0.1, 0.9, "$w$")
plt.text(4.2, 3.1, "$x'$")
plt.text(1.5, 2.4, "$x'^{\Vert w}$")
plt.xticks(np.arange(-3, 15))
plt.yticks(np.arange(-1, 5))
plt.xlim(-3, 7)
plt.ylim(-1, 5)
plt.show()

profile
JKH
Connecting my favorite things
이전 포스트

[Linear algebra] 2.4 선형 연립방정식과 역행렬

다음 포스트

[Linear algebra] 3.2 좌표와 변환

0개의 댓글

관련 채용 정보