다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다
5.2 Properties of determinant
- 이전 시간에, elementary row operation을 하면 det의 값이 바뀐다고 배웠다.
그럼에도 불구하고, 바뀌는 정도가 우리가 tracking하기 좋아서, 충분히 elementary row operation를 통해 원행렬을 좀 더 쉬운 행렬로 바꿔서 det를 구하도록 한다.

(pf1)
- n-1 일때 성립한다고 가정하자. n 일때는 성립할까?
- 어떤 행렬의 특정한 두 row의 위치를 바꾸어서, 서로 다른 행렬을 만들어낸다.
- 위에서 선택한 두 row를 제외한 다른 row를 선택하여, det operation을 진행한다
aCa+bCb+cCc+dCd
이때, cofactor Ca를 계산하기 위해, a가 있는 행,열을 지우고 남은 sub matrix에 대해서 det를 계산 (recursively) - cofactor Ca와 □의 값은 얼마나 다를까?
n-1일 때 성립한다는 성질을 이용하면, □자리에 오는 값은 1번 성질에 의해 (-Ca)가 온다 - 1번 성질 증명 완료
(pf2)
- A는 똑같은 두 개의 행을 가진다.
- 이 두 행의 위치를 바꾼 행렬이 (A|) (A=A|)
(pf3)
(주의)
|cA|=/= c|A|
|cA|= (c^n)|A|
- 4번 성질에 따라 A의 n개의 행에 모두 c를 곱한 것이므로,
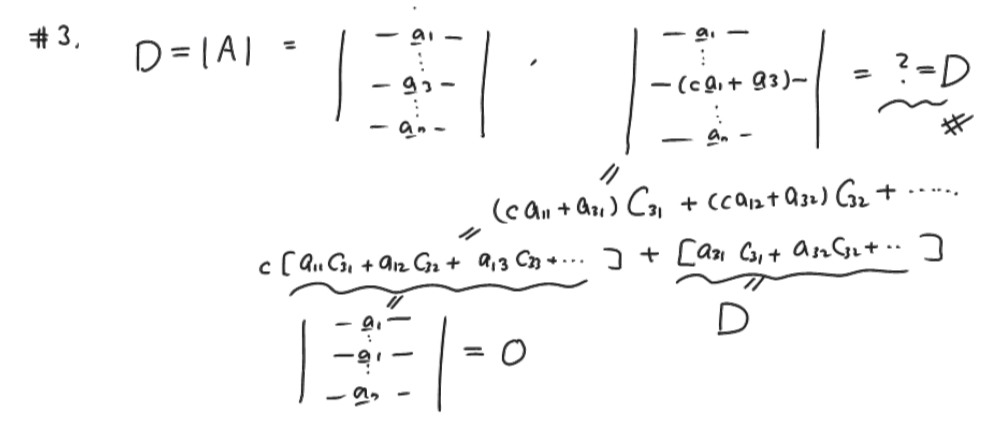
- (pf2)
A(2x2)에 대해서 살펴보고,
A(3x3) 이상에 대해서는, 귀납법으로 살펴본다.
A(n-1xn-1)에 대해서 이 사실이 성립한다고 가정하고, A(nxn)에 대해서 성립한다는 것을 보이자
행 <-> 열 로 바꿔서 생각+ transpose로 생각 - (pf3)
특정 zero row(column)에 대해서 determinant operation을 전개하면 증명 가능 - (pf4)
비례관계 = 상수배
한 row의 상수배는 det의 상수배 이다
해당 비례 상수를 앞으로 끄집어내면, det안의 행렬에는 완전하게 같은 두 행이 존재하게 된다

- (mxn) matrix 안에 (rxr) sub matrix 가 있을 때, 그 submatrix의 det는 0이 아니다(해당 sub matrix가 굳이 뭉쳐 있을 필요는 없다. 흩어져 있어도 된다)
- 조금 덜 지워서 (r+1xr+1) matrix의 det는 0 이다.
- 즉 sub matrix의 크기에 따라 해당 sub matrix의 det의 값은 달라진다
- 이때의 threshold point 가 rank와 같다
(pf)
-
If 주어진 행렬 A(mxn)이 공교롭게도 echelon form으로 쓰여져 있다고 하자 (rank=3)
(1) 위의 theorem에 따르면, det가 nonzero인 3x3 submatrix가 존재한다.
0이 속하는 컬럼을 모두 지우면, 대각선에는 0이 아닌 원소(pivot)이 오는 3x3 submatrix가 남게 된다. 이 행렬의 det는 모든 대각 원소의 곱이므로, 0이 아니다!
(2) r보다 한 차수를 키워서 (r+1xr+1)인 submatrix을 생각해보면, 그 어떠한 submatrix라도 0이 속하게 된다 -
If 주어진 행렬 A(mxn)이 echelon form이 아니라고 하자
행렬 A -> elchelon form으로 만들어서,
(1) 쓸데없는(0이 포함된) 행,열을 확인하고, 이를 원행렬 A에서 지운다.
남는 원소들(초록 동그라미) from 원행렬 -> 남는 원소들(초록 동그라미) from echelon form를 보면,
det(남는 원소들(초록 동그라미) from echelon form) =/=0
elementary row operation 을 하면 det의 값은 바뀌어도, 0으로 바뀌거나, 그 반대가 되지는 않기 때문에,
det(남는 원소들(초록 동그라미) from 원행렬)=/=0
(2) 덜 지우면,
det(남는 원소들(초록 동그라미) from echelon form) =0 (0이 포함되어있으므로)
=> det(남는 원소들(초록 동그라미) from 원행렬) =0 (0이 포함되어있으므로)


