다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다
5.1 Determinant
- determinant : 어떤 행렬이 주어졌을 때, 그 행렬에 대응되는 어떤 real number를 돌려주는 operation
- C(i,j) : cofactor of (i,j)
- 원소 A(i,j)와 곱해지는 값 -> 자릿수 개념
- C(i,j) = (-1) ^(i+j) M(i,j)
- M(i,j) : minor of (i,j)
- A에서 ith row, jth column의 모든 원소를 지운다.
- A의 크기는 (nxn) -> (n-1xn-1)이 된다.
- sub matrix (남은 원소로 이루어진 행렬)의 det값을 이용해서, a11C11 + ... + a1nC1n을 해서 (한 사이즈 큰 행렬의) det값을 구할 수 있게 된다.
- defined recursively

det operation; a11C11 + ... + a1nC1n 에서 각 칼럼의 첫번째 원소의 값만 특별대우를 해주는 걸까?
사실, 굳이 첫번째 원소가 아니어도 된다.
det A = Σ(n, k=1) aik Cik
= Σ(n, k=1) ajk Cjk (j=1,2,...n) -> 각 칼럼의 두번째 값에 대해서 계산해도 가능하다.
- nxn 행렬이 있다
- determinant는 여러 항들의 합인데, 각 항들은 n개의 원소의 곱으로 이루어져있다.
- n개들의 원소는 어떻게 뽑아낼까?
- 첫번째 row에서 하나의 원소를 정했다면, 두번쨰 row에서는 그것과 같은 칼럼에 오지 않는 원소를 뽑고, ~~
- 이렇게 뽑힌 n 개의 원소를 곱하고 ~~
- 모든 가능한 경우의 수를 뽑아서 곱한 후 다 더해도 det가 된다.
- 몇개의 항들의 합으로 이루어져 있을까?
- 첫 번쨰 row에서 원소를 뽑을 수 있는 경우의 수는 n
- 두 번째 row에서 원소를 뽑을 수 있는 경우의 수는 n-1
- 세 번째 row에서 원소를 뽑을 수 있는 경우의 수는 n-2
- n!개의 덧셈을 수행하면 det를 구할 수 있다.
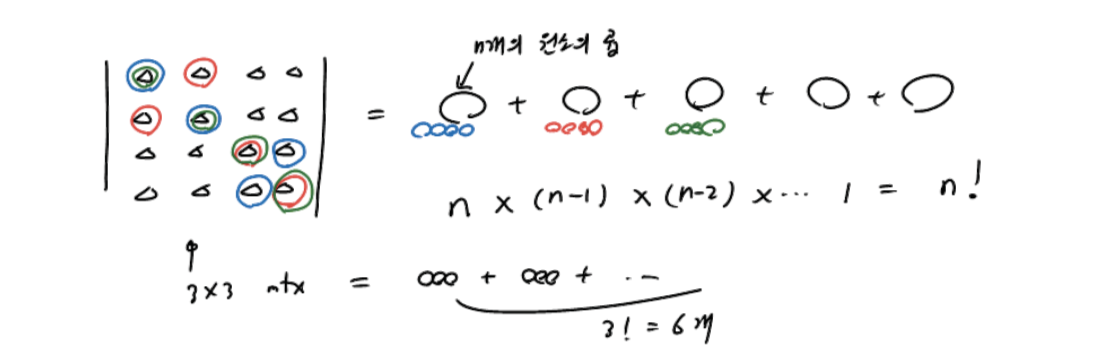
example
- triangular matrix의 det는 대각선의 모든 원소들의 곱이다.
- upper tri mat의 경우에도 동일하다; column을 기준으로 생각해보자
- 잘 생각해보자!
- gauss elimination process 를 통해 rank를 구할 수 있었던 이유는 elementary row operation이 rank를 바꾸지 않았기 때문이다 (그래서 우리가 마음놓고 행렬을 좀 더 쉬운 행렬로 나타내서 rank를 구할 수 있었다)
- 주어진 행렬에 elementary row operation을 해도 det값이 바뀌지 않으면, elementary row operation을 해서 det를 구할 수 있었을 텐데, 그게 아니다ㅠ
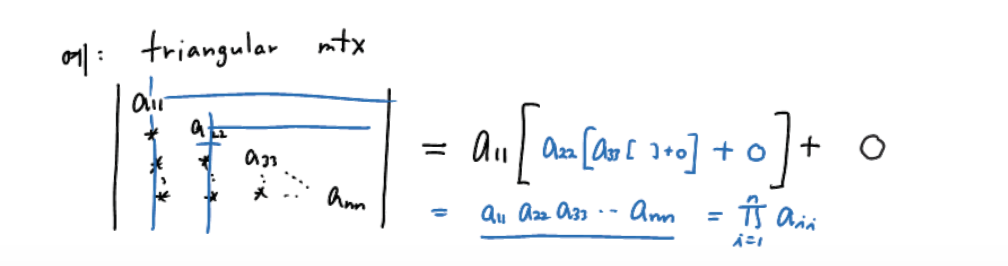
- 잘 생각해보자!
