etl 공학수학1 강의
1.3. Rank of a matrix, Linear independence of vectors(-ing)

다음은 etl.snu의 선형대수학 강의를 듣고 정리한 내용입니다For v1,v2,...,vm ∈ Rn,linear combination; 선형조합c1v1 + c2v2 + ...+cmvm (상수배를 한 벡터끼리 더함)IF c1v1 + c2v2 + ...+cmvm = 0
2.4.1 vector space and its basis
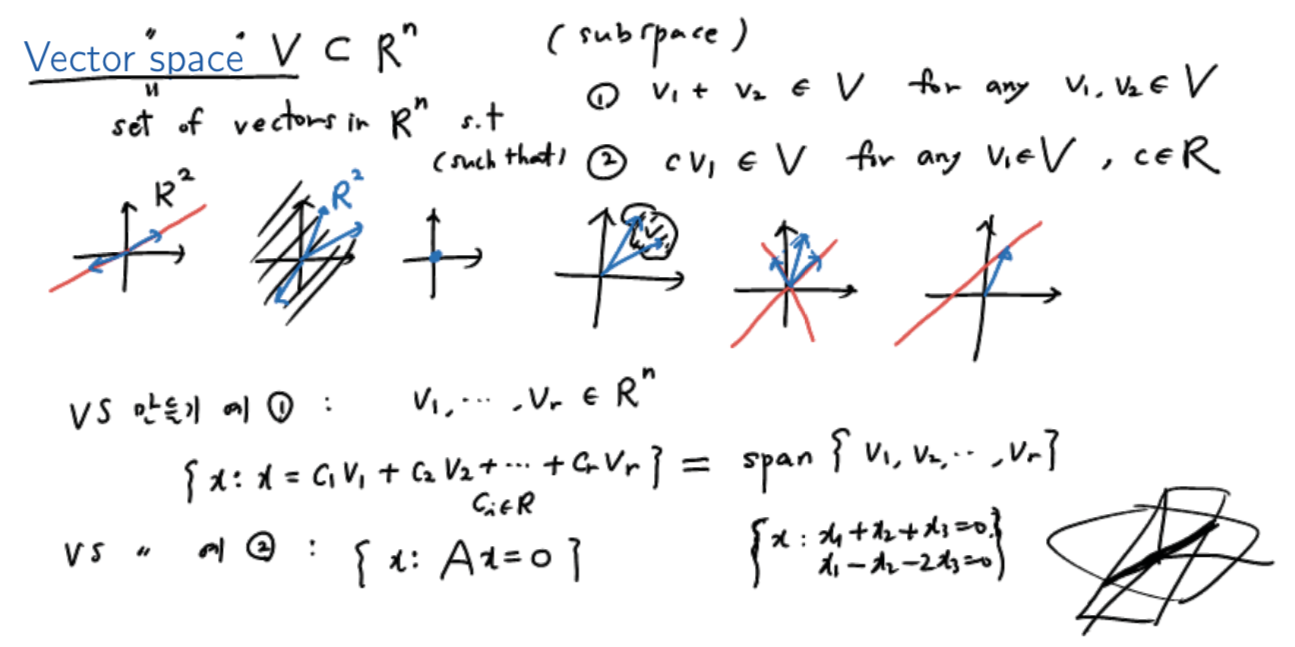
벡터 공간; 벡터들의 "집합"vector space V는 Rn 공간(컬럼 벡터들이 모인)의 부분집합인 벡터 공간굳이 집합이 아닌 "space"라는 말을 쓰는 이유?v1+v2 ∈V for any v1,v2∈ Vcv1 ∈V for any v1∈V, c∈R예1. R2 공간에
3.4.2 Column space and null space

다음은 etl.snu의 선형대수학 강의를 듣고 정리한 내용입니다column들을 선형조합해서 만드는 spaceA∈R(mxn)에 관한 유용한 subspace(vector space)A:Rn에 속하는 임의의 벡터 x에 대해서, y=Ax를 만족하는 모든 y의 집합Ax=a1x1
4.4.3 Existence and uniqueness of solutions

다음은 etl.snu의 선형대수학 강의를 듣고 정리한 내용입니다Existenceb라는 컬럼 벡터는 a라는 컬럼벡터들의 선형조합으로 바꾸어 생각해볼 수 있다.즉, b는 a(i)벡터들에 대해서 독립일 수가 없다 -> b는 역할을 하지 못한다! \-> rankA b =ra
5.4.4 Vector space in general

다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다이제는 Rn 공간에서 벗어나서 좀 더 추상화된 벡터 공간을 생각해보자이때의 벡터는 여러가지 object를 가르킬 수 있다! 마치 라잌 "원소"의 느낌의 term (다항식, 2x2 matrix,...)R2x2
6.5.1 Determinant

다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다determinant : 어떤 행렬이 주어졌을 때, 그 행렬에 대응되는 어떤 real number를 돌려주는 operationC(i,j) : cofactor of (i,j)원소 A(i,j)와 곱해지는 값 -
7.5.2 Properties of determinant

다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다이전 시간에, elementary row operation을 하면 det의 값이 바뀐다고 배웠다.그럼에도 불구하고, 바뀌는 정도가 우리가 tracking하기 좋아서, 충분히 elementary row ope
8.6.1~2 Inverse of a matrix & Gauss-Jordan elimination

다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다
9.6.3 Formula for the inverse & Properties

6.3 Formula for the inverse 6.4 Properties of inverse and nonsingular matrices