references:
https://lovit.github.io/nlp/machine%20learning/2018/10/16/spherical_kmeans/
https://github.com/lovit/clustering4docs
- kmeans 는 유클리드 거리를 기반으로 클러스터링 실행
- 그러나, 문서 클러스터링의 경우, 유클리드 거리가 아닌, 코사인 유사도를 이용하는 것이 더 좋다 → 이러한 코사인 유사도를 이용한 kmeans를 spherical k-means라고 함
why spherical k-means?
(1) why k-means?
- 문서 군집화의 경우, 문서의 개수가 매우 많기 때문에, 다른 클러스터링보다 적은 계산 비용을 요구하는 kmeans가 좋다
- 같은 partition에 속한 데이터 간에는 서로 비슷하며, 서로 다른 partition에 속한 데이터간에는 이질적이도록 만든다.
(2) why cosine distance?
-
BoW model처럼 희소 벡터로 표현되는 고차원 데이터간의 거리를 정의할 때 유클리드 거리는 부적합
→ 벡터의 크기에 영향을 받으므로 -
코사인 유사도
→ 벡터의 크기가 무시됨
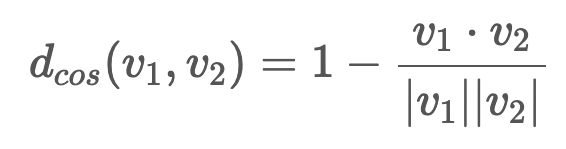
-
고차원의 sparse vectors 간의 거리 척도는 두 벡터에 포함된 공통 성분의 무엇인지를 측정하는 것이 중요하기 때문에 Jaccard distance, Pearson correlation, Cosine distance 와 같은 척도를 쓰면 거리가 잘 정의되나, Euclidean distance 를 이용하면 안된다고 말합니다.
how to construct spherical k-means?
(1) input 으로 입력되는 행렬 x 의 모든 rows 를 unit vectors 로 만들기
(2) centroid update 를 할 때, 벡터의 합을 L2 normalize 하여 centroid 를 unit vector 로 만들기
(기존의 kmeans의 centroid update에서는, 한 군집에 포함된 모든 벡터의 합을 rows 의 개수로 나눔)
→ Lloyd k-means 처럼 한 군집 안의 벡터의 합을 rows 의 개수로 나누는 것은 L1 normalize 의 효과가 있으며, centroid 의 크기가 1 이라는 보장이 없습니다. 그렇기 때문에 다음 번 반복 계산에서 모든 rows 와 centroids 간의 거리를 계산할 때 군집의 centroid vector 의 크기에 영향을 받게 됩니다.
→ 이렇게 두 경우만 바꾸면 Euclidean distance 를 이용하는 것과 Cosine distance 를 이용하는 것이 동일한 학습 결과를 가집니다. 모든 벡터의 크기가 1 이라면 Euclidean distance 기준으로 가장 가까운 벡터는 벡터의 내적이 가장 큰 (Cosine similarity 가 가장 큰) 벡터이기 때문입니다.
