데이터 전처리

LEEEEE·2022년 1월 3일

전처리의 중요성

“데이터 분석의 8할은 데이터 전처리이다.”라는 말이 있다. 그렇다면 왜 데이터 분석에서 전처리가 중요한 것일까?

이유는 전처리에 따라 데이터 분석의 질이 달라지기 때문이다. 전처리가 충분하지 않거나 잘못된 데이터를 사용할 경우 분석 결과의 신뢰도가 떨어지고, 예측 모델의 정확도도 떨어질 것이다. 이런 이유로 전처리가 중요하다.

오늘은 결측치, 중복된 데이터, 이상치, 정규화, 원-핫 인코딩, 구간화에 대해 알아보자!

사용한 데이터

관세청 수출입 무역 통계 사용

결측치(Missing Data)

결측치는 데이터가 누락되어 있는 것을 의미한다. 이런 결측치를 처리하는 방법은 크게 2가지가 있다.

1) 결측치가 있는 데이터를 제거한다.
2) 결측치를 어떤 값으로 대체한다.

결측치를 대체하는 방법은 다양한데 데이터마다 특성을 반영하여 해결해야 한다.

결측치는 전체 데이터 건수에서 각 컬럼별 값이 있는 데이터 수를 빼주면 알 수 있다.

print('컬럼별 결측치 개수')
len(trade) - trade.count()
/------------------------/
# 출력
컬럼별 결측치 개수
기간        0
국가명       0
수출건수      3
수출금액      4
수입건수      3
수입금액      3
무역수지      4
기타사항    199
dtype: int64

기타사항 컬럼이 전부 결측치인 것을 확인할 수 있다. 해당 컬럼을 삭제하려면 .drop('삭제할 컬럼명')을 사용하면 된다.

trade = trade.drop('기타사항', axis=1)
trade.head()
/-----------------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
0	2015년 01월	중국	116932.0	12083947.0	334522.0	8143271.0	3940676.0
1	2015년 01월	미국	65888.0		5561545.0	509564.0	3625062.0	1936484.0
2	2015년 01월	일본	54017.0		2251307.0	82480.0		3827247.0	-1575940.0
3	2015년 02월	중국	86228.0		9927642.0	209100.0	6980874.0	2946768.0
4	2015년 02월	미국	60225.0		5021264.0	428678.0	2998216.0	2023048.0

그렇다면 결측치가 있는 행은 어떻게 확인할까?
DataFrame.isnull()을 이용하면 데이터 별로 결측치 여부를 True, False로 반환한다. DataFrame.any(axis=1)는 행마다 하나라도 True가 있으면 True, 그렇지 않으면 False를 반환한다.

trade.isnull()
/------------/
# 출력
	기간	국가명	수출건수	수출금액	수입건수	수입금액	무역수지
0	False	False	False	False	False	False	False
1	False	False	False	False	False	False	False
2	False	False	False	False	False	False	False
3	False	False	False	False	False	False	False
4	False	False	False	False	False	False	False
...	...	...	...	...	...	...	...
194	False	False	False	False	False	False	False
195	False	False	False	False	False	False	False
196	False	False	True	True	True	True	True
197	False	False	True	True	True	True	True
198	False	False	True	True	True	True	True
199 rows × 7 columns

trade.isnull().any(axis=1)
/------------------------/
# 출력
0      False
1      False
2      False
3      False
4      False
       ...  
194    False
195    False
196     True
197     True
198     True
Length: 199, dtype: bool

trade.isnull().any(axis=1)을 다시 DataFrame에 넣어주면 값이 True인 데이터만 추출해 준다.

trade[trade.isnull().any(axis=1)]
/-------------------------------/
# 출력
	기간		국가명	수출건수	수출금액	수입건수	수입금액	무역수지
191	2020년 04월	미국	105360.0	NaN	1141118.0	5038739.0	NaN
196	2020년 06월	중국	NaN	NaN	NaN	NaN	NaN
197	2020년 06월	미국	NaN	NaN	NaN	NaN	NaN
198	2020년 06월	일본	NaN	NaN	NaN	NaN	NaN

index 191 데이터는 수출금액과 무역수지 컬럼이 빠져있고, index 196, 197, 198은 기간, 국가명을 제외하고 모두 결측치다. 이 경우 index 191 데이터는 삭제하기보다 특정 값으로 대체하는 것이 좋다. 반면 index 196, 197, 198은 제거하는 것이 바람직하다.

DataFrame의 dropna는 결측치를 삭제해 주는 메서드다. subset 옵션으로 특정 컬럼들을 선택했다. how 옵션으로 선택한 컬럼 전부가 결측치인 행을 삭제하겠다는 의미로 'all'을 선택합니다('any': 하나라도 결측치인 경우). inplace 옵션으로 해당 DataFrame 내부에 바로 적용시켜보자.

trade.dropna(how='all', subset=['수출건수', '수출금액', '수입건수', '수입금액', '무역수지'], inplace=True)
print("👽 It's okay, no biggie.")
trade[trade.isnull().any(axis=1)]
/--------------------------------------------------------------------------------------------------/
# 출력
👽 It's okay, no biggie.
	기간		국가명	수출건수		수출금액	수입건수		수입금액		무역수지
191	2020년 04월	미국	105360.0	NaN	1141118.0	5038739.0	NaN

아래는 index 191과 같이 수치형 데이터를 보완할 방법을 제시한다.
1) 특정 값을 지정해 줄 수 있다. 그러나 결측치가 많은 경우, 모두 같은 값으로 대체한다면 데이터의 분산이 실제보다 작아지는 문제가 생길 수 있다.

2) 평균, 중앙값 등으로 대체할 수 있다. 1번에서 특정 값으로 대체했을 때와 마찬가지로 결측치가 많은 경우 데이터의 분산이 실제보다 작아지는 문제가 발생할 수 있다.

3) 다른 데이터를 이용해 예측값으로 대체할 수 있다. 예를 들어 머신러닝 모델로 2020년 4월 미국의 예측값을 만들고, 이 값으로 결측치를 보완할 수 있다.

4) 시계열 특성을 가진 데이터의 경우 앞뒤 데이터를 통해 결측치를 대체할 수 있다. 예를 들어 기온을 측정하는 센서 데이터에서 결측치가 발생할 경우, 전후 데이터의 평균으로 보완할 수 있다.

4번의 방법으로 보완해보자.
DataFrame.loc[행 라벨, 열 라벨]을 입력하면 해당 라벨을 가진 데이터를 출력해준다.

trade.loc[[188, 191, 194]]
/------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
188	2020년 03월	미국	97117.0		7292838.0	1368345.0	5388338.0	1904500.0
191	2020년 04월	미국	105360.0	NaN		1141118.0	5038739.0	NaN
194	2020년 05월	미국	126598.0	4600726.0	1157163.0	4286873.0	313853.0

이전 달과 다음 달의 평균으로 값을 채워보자.

trade.loc[191, '수출금액'] = (trade.loc[188, '수출금액'] + trade.loc[194, '수출금액'] )/2
trade.loc[[191]]
/-----------------------------------------------------------------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
191	2020년 04월	미국	105360.0	5946782.0	1141118.0	5038739.0	NaN

무역수지 컬럼은 수출금액과 수입금액의 차이를 이용하여 채워보자.

trade.loc[191, '무역수지'] = trade.loc[191, '수출금액'] - trade.loc[191, '수입금액'] 
trade.loc[[191]]
/------------------------------------------------------------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
191	2020년 04월	미국	105360.0	5946782.0	1141118.0	5038739.0	908043.0

중복된 데이터

데이터를 수집하는 과정에서 중복된 데이터가 생길 수 있다. 같은 값을 가진 데이터 없이 행(row)별로 값이 유일해야 한다면 중복된 데이터를 제거해야 한다.

trade.duplicated()
/----------------/
# 출력
0      False
1      False
2      False
3      False
4      False
       ...  
191    False
192    False
193    False
194    False
195    False
Length: 196, dtype: bool

trade[trade.duplicated()]
/-----------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
187	2020년 03월	중국	248059.0	10658599.0	358234.0	8948918.0	1709682.0

trade[(trade['기간']=='2020년 03월')&(trade['국가명']=='중국')]
/----------------------------------------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
186	2020년 03월	중국	248059.0	10658599.0	358234.0	8948918.0	1709682.0
187	2020년 03월	중국	248059.0	10658599.0	358234.0	8948918.0	1709682.0

186, 187이 중복되어 있다. pandas에서는 DataFrame.drop_duplicates를 통해 중복된 데이터를 손쉽게 삭제할 수 있다.

trade.drop_duplicates(inplace=True)
print("👽 It's okay, no biggie.")
trade[(trade['기간']=='2020년 03월')&(trade['국가명']=='중국')]
/----------------------------------------------------------/
# 출력
👽 It's okay, no biggie.
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
186	2020년 03월	중국	248059.0	10658599.0	358234.0	8948918.0	1709682.0

아래와 같은 데이터 프레임이 있다고 해보자.

df = pd.DataFrame({'id':['001', '002', '003', '004', '002'], 
                   'name':['Park Yun', 'Kim Sung', 'Park Jin', 'Lee Han', 'Kim Min']})
df
/------------------------------------------------------------------------------------/
# 출력
	id	name
0	001	Park Yun
1	002	Kim Sung
2	003	Park Jin
3	004	Lee Han
4	002	Kim Min

id가 겹치는 데이터가 2개 있다. id 값은 고유한 값이라고 했을 때, 둘 중 하나는 삭제해야한다. 인덱스 값이 클수록 나중에 들어온 데이터이다. 이런 경우에는 나중에 들어온 중복 값만 남겨야한다. DataFrame.drop_duplicates의 subset, keep 옵션을 통해 손쉽게 중복을 제거할 수 있다.
더 자세한 내용은 링크에서 알아보자.

df.drop_duplicates(subset=['id'], keep='last')
/--------------------------------------------/
# 출력
	id	name
0	001	Park Yun
2	003	Park Jin
3	004	Lee Han
4	002	Kim Min

이상치(Outlier)

이상치란 대부분 값의 범위에서 벗어나 극단적으로 크거나 작은 값을 의미한다. Min-Max Scaling 해보면 대부분의 값은 0에 가깝고 이상치만 1에 가까운 값을 가지게 될 것이다. 이런 몇몇의 이상치 때문에 대부분의 값이 의미가 없어지게 된다. 극단적인 값이 생기는 경우를 제외하고 데이터를 고려하고 싶은 경우 이상치를 제거하고 분석한다.

가장 먼저 생각해 볼 수 있는 간단하고 자주 사용되는 방법은 평균과 표준편차를 이용하는 z score 방법이다.

평균을 빼주고 표준편차로 나눠 z score를 계산한다. 그리고 z score가 특정 기준을 넘어서는 데이터에 대해 이상치라고 판단한다. 기준을 작게 하면 이상치라고 판단하는 데이터가 많아지고, 기준을 크게 하면 이상치라고 판단하는 데이터가 적어진다.

이상치 판단 후에는 어떻게 할까?
1) 가장 간단한 방법으로 이상치를 삭제할 수 있다. 이상치를 원래 데이터에서 삭제하고, 이상치끼리 따로 분석하는 방안도 있다.

2) 이상치를 다른 값으로 대체할 수 있다. 데이터가 적으면 이상치를 삭제하기보다 다른 값으로 대체하는 것이 나을 수 있다. 예를 들어 최댓값, 최솟값을 설정해 데이터의 범위를 제한할 수 있다.

3) 혹은 결측치와 마찬가지로 다른 데이터를 활용하여 예측 모델을 만들어 예측값을 활용할 수도 있다.

4) 아니면 binning을 통해 수치형 데이터를 범주형으로 바꿀 수도 있다.

z-score method

이상치인 데이터의 인덱스를 리턴하는 outlier라는 함수를 만들었다. 데이터프레임 df, 컬럼 col, 기준 z를 인풋으로 받는다.

abs(df[col] - np.mean(df[col])) : 데이터에서 평균을 빼준 것에 절대값을 취한다.
abs(df[col] - np.mean(df[col]))/np.std(df[col]) : 위에 한 작업에 표준편차로 나눠준다.
df[abs(df[col] - np.mean(df[col]))/np.std(df[col])>z].index : 값이 z보다 큰 데이터의 인덱스를 추출한다.

def outlier(df, col, z):
    return df[abs(df[col] - np.mean(df[col]))/np.std(df[col])>z].index
print("👽 It's okay, no biggie.")
trade.loc[outlier(trade, '무역수지', 1.5)]
/---------------------------------------------------------------------/
# 출력
👽 It's okay, no biggie.
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
6	2015년 03월	중국	117529.0	11868032.0	234321.0	7226911.0	4641121.0
75	2017년 02월	중국	159062.0	11118131.0	188555.0	6600637.0	4517495.0
80	2017년 03월	일본	65093.0		2395932.0	165734.0	5157589.0	-2761657.0
96	2017년 09월	중국	183442.0	13540683.0	295443.0	8443414.0	5097269.0
99	2017년 10월	중국	137873.0	12580474.0	244977.0	7932403.0	4648071.0
101	2017년 10월	일본	63510.0		1847999.0	127696.0	4418583.0	-2570584.0
102	2017년 11월	중국	421194.0	14000887.0	307790.0	9253318.0	4747569.0
105	2017년 12월	중국	218114.0	13848364.0	290347.0	8600132.0	5248232.0
114	2018년 03월	중국	232396.0	13576667.0	267249.0	8412516.0	5164151.0
116	2018년 03월	일본	80142.0		2603450.0	159601.0	5226141.0	-2622691.0
120	2018년 05월	중국	214145.0	13851900.0	307183.0	9279720.0	4572180.0
123	2018년 06월	중국	257130.0	13814241.0	279023.0	8713018.0	5101223.0
126	2018년 07월	중국	181772.0	13721233.0	293164.0	8869278.0	4851955.0
129	2018년 08월	중국	199010.0	14401521.0	280033.0	8525532.0	5875989.0
132	2018년 09월	중국	171328.0	14590529.0	280337.0	7889890.0	6700639.0
135	2018년 10월	중국	169809.0	14767041.0	319876.0	9963108.0	4803932.0

trade.loc[outlier(trade, '무역수지', 2)]
/-------------------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
129	2018년 08월	중국	199010.0	14401521.0	280033.0	8525532.0	5875989.0
132	2018년 09월	중국	171328.0	14590529.0	280337.0	7889890.0	6700639.0

trade.loc[outlier(trade, '무역수지', 3)]
/-------------------------------------/
# 출력
기간	국가명	수출건수	수출금액	수입건수	수입금액	무역수지

무역수지의 이상치를 확인하는데 기준 되는 값이 클수록 이상치가 적어지는 것을 확인할 수 있다.
이제 not_outlier라는 함수를 통해 무역수지가 이상치 값이 아닌 데이터만 추출하도록 한다.

def not_outlier(df, col, z):
    return df[abs(df[col] - np.mean(df[col]))/np.std(df[col]) <= z].index
print("👽 It's okay, no biggie.")
trade.loc[not_outlier(trade, '무역수지', 1.5)]
/-----------------------------------------------------------------------/
# 출력
👽 It's okay, no biggie.
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
0	2015년 01월	중국	116932.0	12083947.0	334522.0	8143271.0	3940676.0
1	2015년 01월	미국	65888.0		5561545.0	509564.0	3625062.0	1936484.0
2	2015년 01월	일본	54017.0		2251307.0	82480.0		3827247.0	-1575940.0
3	2015년 02월	중국	86228.0		9927642.0	209100.0	6980874.0	2946768.0
4	2015년 02월	미국	60225.0		5021264.0	428678.0	2998216.0	2023048.0
...	...	...	...	...	...	...	...
191	2020년 04월	미국	105360.0	5946782.0	1141118.0	5038739.0	-1.0
192	2020년 04월	일본	134118.0	1989323.0	141207.0	3989562.0	-2000239.0
193	2020년 05월	중국	185320.0	10746069.0	349007.0	8989920.0	1756149.0
194	2020년 05월	미국	126598.0	4600726.0	1157163.0	4286873.0	313853.0
195	2020년 05월	일본	166568.0	1798128.0	133763.0	3102734.0	-1304606.0
179 rows × 7 columns

IRQ method

z-score 방법은 몇 가지 뚜렷한 한계점을 가지고 있다. z-score 방법의 대안으로 사분위 범위수 IQR(Interquartile range) 로 이상치를 알아내는 방법을 알아보자.

np.random.seed(2020)
data = np.random.randn(100)  # 평균 0, 표준편차 1의 분포에서 100개의 숫자를 샘플링한 데이터 생성
data = np.concatenate((data, np.array([8, 10, -3, -5])))      # [8, 10, -3, -5])를 데이터 뒤에 추가함
data
/------------------------------------------------------------------------------------------------/
# 출력
array([-1.76884571,  0.07555227, -1.1306297 , -0.65143017, -0.89311563,
       -1.27410098, -0.06115443,  0.06451384,  0.41011295, -0.57288249,
       -0.80133362,  1.31203519,  1.27469887, -1.2143576 ,  0.31371941,
       -1.44482142, -0.3689613 , -0.76922658,  0.3926161 ,  0.05729383,
        2.08997884,  0.04197131, -0.04834072, -0.51315392, -0.08458928,
       -1.21545008, -1.41293073, -1.48691055,  0.38222486,  0.937673  ,
        1.77267804,  0.87882801,  0.33171912, -0.30603567,  1.24026615,
       -0.21562684,  0.15592948,  0.09805553,  0.83209585,  2.04520542,
       -0.31681392, -1.31283291, -1.75445746,  0.10209408, -1.36150208,
        0.48178488, -0.20832874, -0.09186351,  0.70268816,  0.10365506,
        0.62123638,  0.95411497,  2.03781352, -0.48445122,  0.2071549 ,
        1.64424216, -0.4882074 , -0.01782826,  0.46891556,  0.27987266,
       -0.64664972, -0.54406002, -0.16008985,  0.03781172,  1.03383296,
       -1.23096117, -1.24673665,  0.29572055,  2.1409624 , -0.92020227,
       -0.06000238,  0.27978391, -1.53126966, -0.30293101, -0.14601413,
        0.27746159, -0.13952066,  0.69515966, -0.11338746, -1.233267  ,
       -0.79614131, -0.46739138,  0.65890607, -0.41063115,  0.17344356,
        0.28946174,  1.03451736,  1.22661712,  1.71998252,  0.40806834,
        0.32256894,  1.04722748, -1.8196003 , -0.42582157,  0.12454883,
        2.31256634, -0.96557586, -0.34627486,  0.96668378, -0.92550192,
        8.        , 10.        , -3.        , -5.        ])

fig, ax = plt.subplots()
ax.boxplot(data)
plt.show()
/----------------------/
# 출력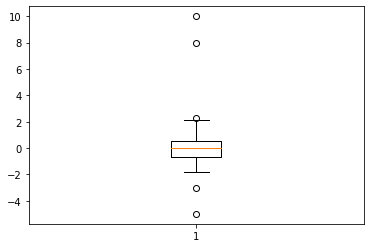

우리는 사분위 범위수 IQR(Interquartile range)을 이용하여 이상치를 찾아낼 수 있다.
즉, IQR은 제 3사분위수에서 제 1사분위 값을 뺀 값으로 데이터의 중간 50%의 범위라고 생각하면 된다.

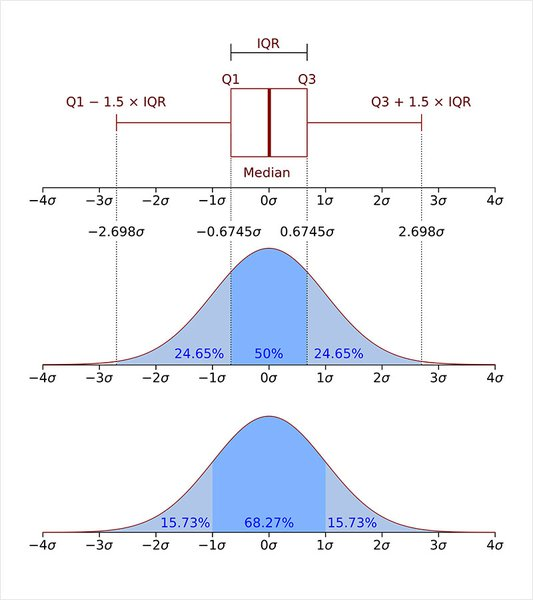
[출처 : https://en.wikipedia.org/wiki/Interquartile_range]

IQR을 구하기 위해 우선 제1사분위수와 제 3사분위수를 구한다.

Q3, Q1 = np.percentile(data, [75 ,25])
IQR = Q3 - Q1
IQR
/------------------------------------/
# 출력
1.1644925829790964

data[(Q1-1.5*IQR > data)|(Q3+1.5*IQR < data)]
/-------------------------------------------/
# 출력
array([ 2.31256634,  8.        , 10.        , -3.        , -5.        ])

링크를 보면 이상치에 대한 것을 알 수 있다.

정규화(Normalization)

trade 데이터를 보면 수입건수, 수출건수와 수입금액, 수출금액, 무역수지는 단위가 다르다는 것을 알 수 있다.
이처럼 컬럼마다 스케일이 크게 차이가 나는 데이터를 입력하면 머신러닝 모델 학습에 문제가 발생할 수 있다. 그래서 일반적으로 컬럼 간에 범위가 크게 다를 경우 전처리 과정에서 데이터를 정규화한다.

정규화를 하는 방법은 다양하지만, 가장 잘 알려진 표준화(Standardization)와 Min-Max Scaling을 알아보도록 하자.

Standardization 데이터의 평균은 0, 분산은 1로 변환
Min-Max Scaling 데이터의 최솟값은 0, 최댓값은 1로 변환

x = pd.DataFrame({'A': np.random.randn(100)*4+4,
                 'B': np.random.randn(100)-1})
x
/----------------------------------------------/
# 출력
	A		B
0	6.205792	-1.485248
1	-0.604047	-0.727779
2	3.018785	-0.517099
3	3.323325	-0.414949
4	6.167679	-0.582630
...	...	...
95	5.062917	-1.122239
96	-0.166839	-2.487547
97	-4.230178	0.589513
98	-0.562115	0.779614
99	5.984528	-1.724450

100 rows × 2 columns

# 데이터 x를 Standardization 기법으로 정규화합니다. 
x_standardization = (x - x.mean())/x.std()
x_standardization
/--------------------------------------------/
# 출력
	A		B
0	0.559307	-0.314995
1	-1.132240	0.407499
2	-0.232338	0.608450
3	-0.156691	0.705884
4	0.549839	0.545945
...	...	...
95	0.275419	0.031252
96	-1.023639	-1.271014
97	-2.032961	1.663966
98	-1.121824	1.845290
99	0.504345	-0.543153

100 rows × 2 columns

# 데이터 x를 min-max scaling 기법으로 정규화합니다. 
x_min_max = (x-x.min())/(x.max()-x.min())
x_min_max
/---------------------------------------------/
# 출력
	A		B
0	0.607216	0.426240
1	0.267692	0.571821
2	0.448318	0.612312
3	0.463502	0.631944
4	0.605316	0.599717
...	...	...
95	0.550235	0.496008
96	0.289490	0.233606
97	0.086901	0.824995
98	0.269782	0.861531
99	0.596184	0.380268

100 rows × 2 columns

다음 이미지는 데이터를 Standardization 기법으로 정규화를 했을 때 분포가 어떻게 바뀌는지 보여준다. 즉, 각 컬럼의 평균은 0으로, 분산은 1로 데이터를 바꿔준다.

fig, axs = plt.subplots(1,2, figsize=(12, 4),
                        gridspec_kw={'width_ratios': [2, 1]})

axs[0].scatter(x['A'], x['B'])
axs[0].set_xlim(-5, 15)
axs[0].set_ylim(-5, 5)
axs[0].axvline(c='grey', lw=1)
axs[0].axhline(c='grey', lw=1)
axs[0].set_title('Original Data')

axs[1].scatter(x_standardization['A'], x_standardization['B'])
axs[1].set_xlim(-5, 5)
axs[1].set_ylim(-5, 5)
axs[1].axvline(c='grey', lw=1)
axs[1].axhline(c='grey', lw=1)
axs[1].set_title('Data after standardization')

plt.show()
/------------------------------------------------------------/
# 출력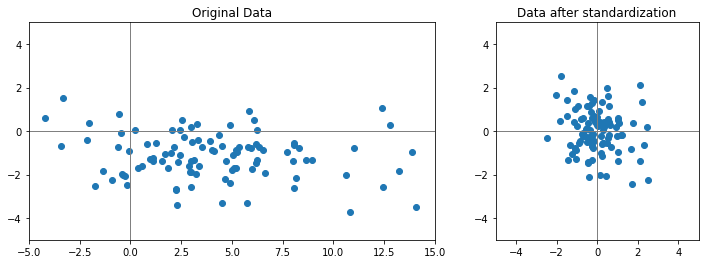

다음 이미지는 동일한 데이터를 min-max scaling 기법으로 정규화를 했을 때 분포가 어떻게 바뀌는지 보여준다. 즉, 각 컬럼의 최솟값은 0, 최댓값은 1로 바꿔준다.

fig, axs = plt.subplots(1,2, figsize=(12, 4),
                        gridspec_kw={'width_ratios': [2, 1]})

axs[0].scatter(x['A'], x['B'])
axs[0].set_xlim(-5, 15)
axs[0].set_ylim(-5, 5)
axs[0].axvline(c='grey', lw=1)
axs[0].axhline(c='grey', lw=1)
axs[0].set_title('Original Data')

axs[1].scatter(x_min_max['A'], x_min_max['B'])
axs[1].set_xlim(-5, 5)
axs[1].set_ylim(-5, 5)
axs[1].axvline(c='grey', lw=1)
axs[1].axhline(c='grey', lw=1)
axs[1].set_title('Data after min-max scaling')

plt.show()
/-----------------------------------------------------------/
# 출력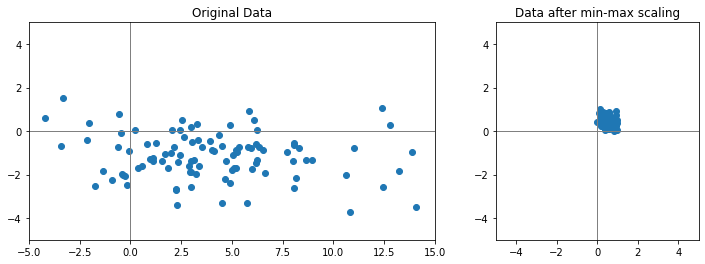

Standardization

우선 정규화를 시켜야 할 수치형 컬럼들을 cols 변수에 담은 후, 데이터에서 평균을 빼고, 표준편차로 나눠주도록 하자.

# trade 데이터를 Standardization 기법으로 정규화합니다. 
cols = ['수출건수', '수출금액', '수입건수', '수입금액', '무역수지']
trade_Standardization= (trade[cols]-trade[cols].mean())/trade[cols].std()
trade_Standardization.head()
/----------------------------------------------------------/
# 출력
	수출건수		수출금액		수입건수		수입금액		무역수지
0	-0.007488	1.398931	-0.163593	1.283660	1.257750
1	-0.689278	-0.252848	0.412529	-0.964444	0.402889
2	-0.847838	-1.091156	-0.993148	-0.863844	-1.095288
3	-0.417598	0.852853	-0.576399	0.705292	0.833812
4	-0.764918	-0.389673	0.146306	-1.276341	0.439812

standardization 방법으로 정규화시킨 trade_Standardization을 확인해 보자. 각 컬럼의 평균들을 보면 거의 0에 가깝고, 표준편차는 1에 가까운 것을 확인할 수 있다.

trade_Standardization.describe()
/------------------------------/
# 출력
	수출건수		수출금액		수입건수		수입금액		무역수지
count	1.950000e+02	1.950000e+02	1.950000e+02	1.950000e+02	1.950000e+02
mean	-1.093143e-16	6.832142e-17	1.821904e-17	-5.465713e-17	-1.821904e-17
std	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00
min	-9.194976e-01	-1.231761e+00	-9.984408e-01	-1.276341e+00	-1.601039e+00
25%	-5.937426e-01	-1.041338e+00	-7.673625e-01	-7.911669e-01	-1.114265e+00
50%	-4.373265e-01	-1.564700e-01	-3.429346e-01	-4.137392e-01	1.446030e-01
75%	4.420459e-01	1.037200e+00	3.927781e-01	8.827841e-01	7.478066e-01
max	5.486317e+00	2.078416e+00	3.239068e+00	2.376092e+00	2.434975e+00

Min-Max Scaling

데이터에서 최솟값을 빼주고, '최댓값-최솟값'으로 나눠준다.

# trade 데이터를 min-max scaling 기법으로 정규화합니다. 
trade[cols] = (trade[cols]-trade[cols].min())/(trade[cols].max()-trade[cols].min())
trade.head()
/---------------------------------------------------------------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지
0	2015년 01월	중국	0.142372	0.794728	0.197014	0.700903	0.708320
1	2015년 01월	미국	0.035939	0.295728	0.332972	0.085394	0.496512
2	2015년 01월	일본	0.011187	0.042477	0.001249	0.112938	0.125310
3	2015년 02월	중국	0.078351	0.629759	0.099597	0.542551	0.603281
4	2015년 02월	미국	0.024131	0.254394	0.270146	0.000000	0.505660

Min-Max Scaling 방법으로 정규화시킨 후, 각 컬럼의 최솟값(min)은 0이고, 최댓값(max)은 1임을 확인할 수 있다.

trade.describe()
/--------------/
# 출력
	수출건수		수출금액		수입건수		수입금액		무역수지
count	195.000000	195.000000	195.000000	195.000000	195.000000
mean	0.143541	0.372113	0.235620	0.349450	0.396688
std	0.156108	0.302099	0.235988	0.273790	0.247769
min	0.000000	0.000000	0.000000	0.000000	0.000000
25%	0.050853	0.057527	0.054532	0.132836	0.120608
50%	0.075271	0.324844	0.154691	0.236172	0.432516
75%	0.212548	0.685450	0.328311	0.591147	0.581972
max	1.000000	1.000000	1.000000	1.000000	1.000000

❗주의

train 데이터와 test 데이터가 나눠져 있는 경우 train 데이터를 정규화시켰던 기준 그대로 test 데이터도 정규화 시켜줘야 한다.

train = pd.DataFrame([[10, -10], [30, 10], [50, 0]])
test = pd.DataFrame([[0, 1], [10, 10]])

train_min = train.min()
train_max = train.max()

train_min_max = (train - train_min)/(train_max - train_min)
test_min_max =  (test - train_min)/(train_max - train_min)    # test를 min-max scaling할 때도 train 정규화 기준으로 수행
train_min_max
/-----------------------------------------------------------------------------------------------------------------/
# 출력
	0	1
0	0.0	0.0
1	0.5	1.0
2	1.0	0.5

test_min_max
/----------/
# 출력
	0	1
0	-0.25	0.55
1	0.00	1.00

scikit-learn의 StandardScaler, MinMaxScaler를 사용하는 방법도 있다.

from sklearn.preprocessing import MinMaxScaler
train = [[10, -10], [30, 10], [50, 0]]
test = [[0, 1]]
scaler = MinMaxScaler()
scaler.fit_transform(train)
/--------------------------------------------/
# 출력
array([[0. , 0. ],
       [0.5, 1. ],
       [1. , 0.5]])

scaler.transform(test)
/--------------------/
# 출력
array([[-0.25,  0.55]])

원-핫 인코딩(One-Hot Encoding)

머신러닝이나 딥러닝 프레임워크에서 범주형을 지원하지 않는 경우 원-핫 인코딩을 해야한다.
원-핫 인코딩이란 카테고리별 이진 특성을 만들어 해당하는 특성만 1, 나머지는 0으로 만드는 방법이다.

pandas에서 get_dummies 함수를 통해 손쉽게 원-핫 인코딩을 할 수 있다.

#trade 데이터의 국가명 컬럼 원본
print(trade['국가명'].head())  

# get_dummies를 통해 국가명 원-핫 인코딩
country = pd.get_dummies(trade['국가명'])
country.head()
/---------------------------------------/
# 출력
0    중국
1    미국
2    일본
3    중국
4    미국
Name: 국가명, dtype: object
	미국	일본	중국
0	0	0	1
1	1	0	0
2	0	1	0
3	0	0	1
4	1	0	0

pd.concat 함수로 데이터프레임 trade와 country를 합쳐준다.

trade = pd.concat([trade, country], axis=1)
trade.head()
/------------------------------------------/
# 출력
	기간		국가명	수출건수		수출금액		수입건수		수입금액		무역수지		미국	일본	중국
0	2015년 01월	중국	0.142372	0.794728	0.197014	0.700903	0.708320	0	0	1
1	2015년 01월	미국	0.035939	0.295728	0.332972	0.085394	0.496512	1	0	0
2	2015년 01월	일본	0.011187	0.042477	0.001249	0.112938	0.125310	0	1	0
3	2015년 02월	중국	0.078351	0.629759	0.099597	0.542551	0.603281	0	0	1
4	2015년 02월	미국	0.024131	0.254394	0.270146	0.000000	0.505660	1	0	0

이제 필요없어진 국가명 컬럼을 삭제한다.

trade.drop(['국가명'], axis=1, inplace=True)
trade.head()
/-----------------------------------------/
# 출력
	기간		수출건수		수출금액		수입건수		수입금액		무역수지		미국	일본	중국
0	2015년 01월	0.142372	0.794728	0.197014	0.700903	0.708320	0	0	1
1	2015년 01월	0.035939	0.295728	0.332972	0.085394	0.496512	1	0	0
2	2015년 01월	0.011187	0.042477	0.001249	0.112938	0.125310	0	1	0
3	2015년 02월	0.078351	0.629759	0.099597	0.542551	0.603281	0	0	1
4	2015년 02월	0.024131	0.254394	0.270146	0.000000	0.505660	1	0	0

구간화(Binning)

데이터를 구간별로 나누는 것을 구간화라고 한다.
소득 데이터 셋이 있다고 하자.

salary = pd.Series([4300, 8370, 1750, 3830, 1840, 4220, 3020, 2290, 4740, 4600, 
                    2860, 3400, 4800, 4470, 2440, 4530, 4850, 4850, 4760, 4500, 
                    4640, 3000, 1880, 4880, 2240, 4750, 2750, 2810, 3100, 4290, 
                    1540, 2870, 1780, 4670, 4150, 2010, 3580, 1610, 2930, 4300, 
                    2740, 1680, 3490, 4350, 1680, 6420, 8740, 8980, 9080, 3990, 
                    4960, 3700, 9600, 9330, 5600, 4100, 1770, 8280, 3120, 1950, 
                    4210, 2020, 3820, 3170, 6330, 2570, 6940, 8610, 5060, 6370,
                    9080, 3760, 8060, 2500, 4660, 1770, 9220, 3380, 2490, 3450, 
                    1960, 7210, 5810, 9450, 8910, 3470, 7350, 8410, 7520, 9610, 
                    5150, 2630, 5610, 2750, 7050, 3350, 9450, 7140, 4170, 3090])

salary.hist()
/------------------------------------------------------------------------------/
# 출력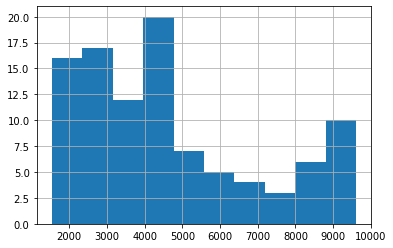

pandas의 cut과 qcut을 이용해 수치형 데이터를 범주형 데이터로 변형시키도록 한다.

cut을 사용하기 위해서는 구간을 정해준다.

bins = [0, 2000, 4000, 6000, 8000, 10000]
ctg = pd.cut(salary, bins=bins)
ctg
/---------------------------------------/
# 출력
0      (4000, 6000]
1     (8000, 10000]
2         (0, 2000]
3      (2000, 4000]
4         (0, 2000]
          ...      
95     (2000, 4000]
96    (8000, 10000]
97     (6000, 8000]
98     (4000, 6000]
99     (2000, 4000]
Length: 100, dtype: category
Categories (5, interval[int64, right]): [(0, 2000] < (2000, 4000] < (4000, 6000] < (6000, 8000] < (8000, 10000]]

salary[0]는 4300으로 4000에서 6000 사이에 포함되었다는 것을 확인할 수 있다.

print('salary[0]:', salary[0])
print('salary[0]가 속한 카테고리:', ctg[0])
/---------------------------------------/
# 출력
salary[0]: 4300
salary[0]가 속한 카테고리: (4000, 6000]

구간별로 값이 몇 개가 속해 있는지 value_counts()로 확인해보자.

ctg.value_counts().sort_index()
/-----------------------------/
# 출력
(0, 2000]        12
(2000, 4000]     34
(4000, 6000]     29
(6000, 8000]      9
(8000, 10000]    16
dtype: int64

이렇게 특정 구간을 지정해 줘도 되고, 구간의 개수를 지정해 줄 수도 있다. bins 옵션에 정수를 입력하면 데이터의 최솟값에서 최댓값을 균등하게 bins 개수만큼 나눠준다.

ctg = pd.cut(salary, bins=6)
ctg
/--------------------------/
# 출력
0      (4230.0, 5575.0]
1      (8265.0, 9610.0]
2     (1531.93, 2885.0]
3      (2885.0, 4230.0]
4     (1531.93, 2885.0]
            ...        
95     (2885.0, 4230.0]
96     (8265.0, 9610.0]
97     (6920.0, 8265.0]
98     (2885.0, 4230.0]
99     (2885.0, 4230.0]
Length: 100, dtype: category
Categories (6, interval[float64, right]): [(1531.93, 2885.0] < (2885.0, 4230.0] < (4230.0, 5575.0] < (5575.0, 6920.0] < (6920.0, 8265.0] < (8265.0, 9610.0]]

ctg.value_counts().sort_index()
/-----------------------------/
# 출력
(1531.93, 2885.0]    27
(2885.0, 4230.0]     24
(4230.0, 5575.0]     21
(5575.0, 6920.0]      6
(6920.0, 8265.0]      7
(8265.0, 9610.0]     15
dtype: int64

qcut은 구간을 일정하게 나누는 것이 아니라 데이터의 분포를 비슷한 크기의 그룹으로 나눠준다.

ctg = pd.qcut(salary, q=5)
ctg
/------------------------/
# 출력
0       (3544.0, 4648.0]
1       (7068.0, 9610.0]
2     (1539.999, 2618.0]
3       (3544.0, 4648.0]
4     (1539.999, 2618.0]
             ...        
95      (2618.0, 3544.0]
96      (7068.0, 9610.0]
97      (7068.0, 9610.0]
98      (3544.0, 4648.0]
99      (2618.0, 3544.0]
Length: 100, dtype: category
Categories (5, interval[float64, right]): [(1539.999, 2618.0] < (2618.0, 3544.0] < (3544.0, 4648.0] < (4648.0, 7068.0] < (7068.0, 9610.0]]

print(ctg.value_counts().sort_index())
print(".\n.\n🛸 Well done!")
/------------------------------------/
# 출력
(1539.999, 2618.0]    20
(2618.0, 3544.0]      20
(3544.0, 4648.0]      20
(4648.0, 7068.0]      20
(7068.0, 9610.0]      20
dtype: int64
.
.
🛸 Well done!