1. Spline곡선의 종류와 성질

• 부드러운 곡선의 모양을 3차 이상의 다항식으로 표현
  • 제어점(Control Point)을 지정하여 곡선의 형태를 생성
  • 3차 이상의 곡선을 미지수가 4개이니, 4개 이상의 조건이 주어짐

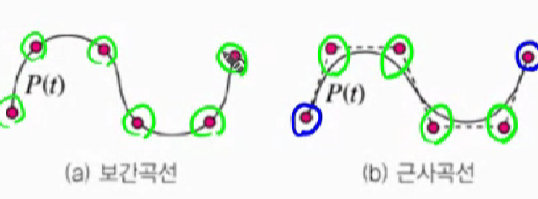
1.1 보간 곡선과 근사 곡선

조건을 어떻게 주느냐에 따라 다른 곡선이 만들어진다.

• 보간 (Interpolation) : 주어진 제어점을 통과
  • Hermite, Cardinal
• 근사 (Approximation) : 제어점을 연결하는 선의 모양에 근사
  • Bezier, NURBS

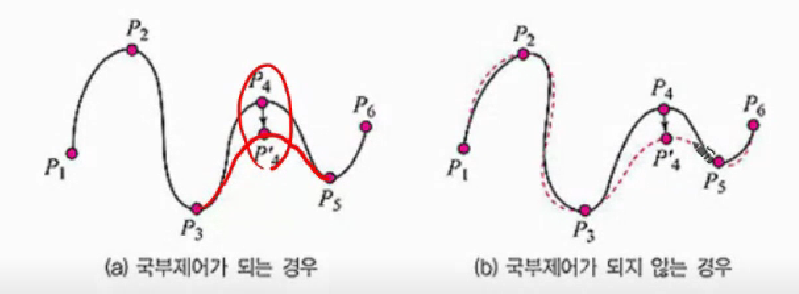
1.2 곡선의 국부제어

• 국부제어 : 제어점 하나가 바뀔 때 영향을 미치는 부분

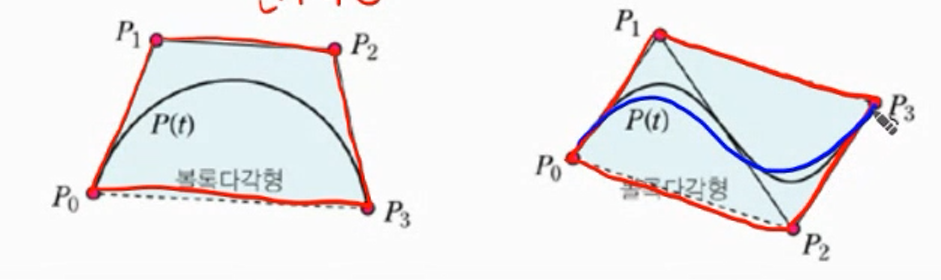
1.3 볼록다각형(Convex Hull) 내포성

• 곡선은 항상 Convex Hull 내에 포함
  • 보간 곡선은 convex hull 내포성을 포함하지 않음
  • 근사 곡선은 만족
• 곡선의 개활적인 모양을 파악, 곡선 클라핑에도 이용

1.4 3차 스플라인 곡선

y = ax^3 + bx^2 + cx + d
f(x) = ax^3 + bx^2 + cx + d

• 미지수(unknown parameters)가 4개, 조건도 4개가 주어짐
• 연속성(continuity,조건)
  • C^0 연속성 : 두 곡선이 단순히 연결, 양쪽 곡선의 좌표값이 동일
  • C^1 연속성 : 곡선의 기울기가 동일, 즉, 1차 도함수가 동일
  • C^2 연속성 : 양쪽 곡선의 곡률이 동일, 1차 및 2차 도함수가 동일
    
• spline curve
  1) 2차원
  

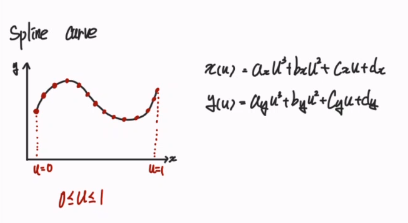
2. Hermite

• 보간 곡선
• C^0 : 2개, C^1 : 2개
• x(0), x(1), x'(0) = dx, x'(1) = dx이 주어짐
• 보간곡선은 구간마다 독립적으로 수행, u[0,1]
  • 한 구간 : u = 0, u = 1 인 부분

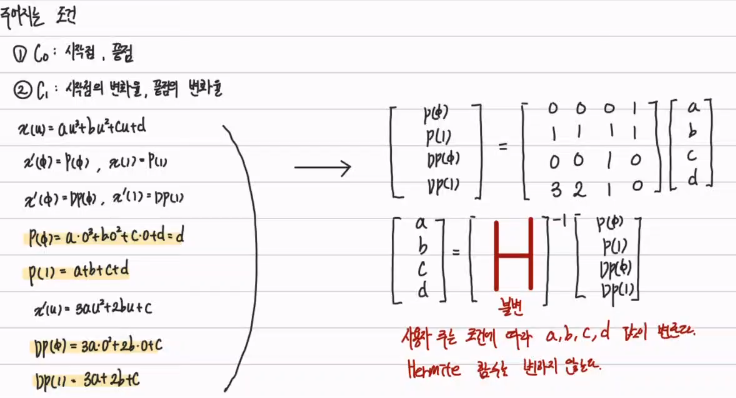
3. Beizer

• 근사 곡선
• Blending function로 이항정리 함수를 사용
• 연속성이 주어지지 않음
• 좌표 값으로만 계산
• 전체 구간에서 u=[0,1]
  

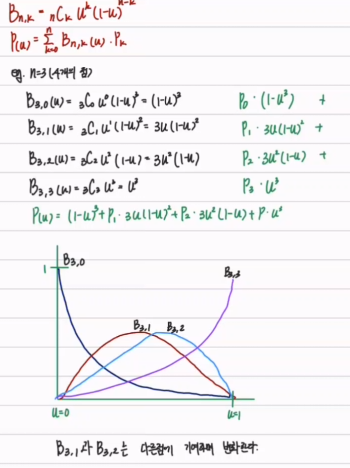
4. B-Spline

4.1 Uniform B-Spline

동일한 curve를 점마다 배치

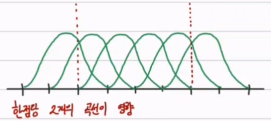
4.2 None-Uniform Rotation B-Spline (NURBS)

간격과 weight가 불변

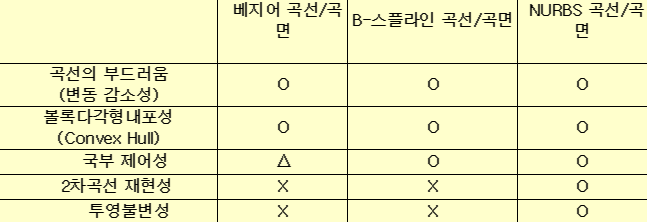
5. 곡선 비교