프랙탈의 생성원리는 임의적 반복 알고리즘에 있다. 규칙을 몇 가지 정한 후 무작위로 규칙을 반복적용하는 방식이다. 따라서 자기 순환적 복제를 한다는 특징이 있다.
P1 = F(P0)
P2 = F(P1)
P3 = F(P2)
P4 = F(P3) ...1. 자기 유사 Fractal
1.1. Koch curve(점 좌표 -> 선)
- 자기자신의 1/3, 2/3 지점에 점 좌표를 추가한 뒤 그 점들에서 기울기가 60인 직선을 그려 만나는 점 좌표를 하나 더 추가하는 방식이다.
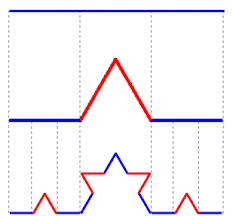
- 구현 코드
void kochcurve(int depth) {
int i;
int pointNum = 9;
//깊이 만큼 반복한다.
for (int step = 0; step < depth; step++)
{
//점의 수가 Point의 3배 만큼 더 많아지니 더해준다.(나는 Cycle로 초기점을 줘서 하나빼줬다.)
pointNum += (pointNum - 1) * 3;
//증가된 점 수만큼 초기점의 index를 띄어준다.
for (int i = 0; i < pointNum; i += 4) {
temp[i].x = point_koch[i / 4].x;
temp[i].y = point_koch[i / 4].y;
}
//새 점을 그리는 반복문
for (int i = 0; i < pointNum; i++) {
//1/3, 2/3 지점을 구해준다.
if ((i % 4) == 1)
{
temp[i].x = temp[i - 1].x + (temp[i + 3].x - temp[i - 1].x) / 3;
temp[i].y = temp[i - 1].y + (temp[i + 3].y - temp[i - 1].y) / 3;
temp[i + 2].x = temp[i + 3].x - (temp[i + 3].x - temp[i - 1].x) / 3;
temp[i + 2].y = temp[i + 3].y - (temp[i + 3].y - temp[i - 1].y) / 3;
}
//중간점을 cos(60), sin(60)으로 구해준다.
else if ((i % 4) == 2)
{
temp[i].x = (cos(radian(60)) * (temp[i + 1].x - temp[i - 1].x) - sin(radian(60)) * (temp[i + 1].y - temp[i - 1].y)) + temp[i - 1].x;
temp[i].y = (sin(radian(60)) * (temp[i + 1].x - temp[i - 1].x) + cos(radian(60)) * (temp[i + 1].y - temp[i - 1].y)) + temp[i - 1].y;
}
point_koch[i].x = temp[i].x;
point_koch[i].y = temp[i].y;
}
}
//다 그린 점을 이어준다.(DDA알고리즘은 단순하니 생략함)
for (i = 0; i < pointNum - 1; i++) {
lineDDA((int)(point_koch[i].x + 0.5), (int)(point_koch[i].y + 0.5), (int)(point_koch[i + 1].x + 0.5), (int)(point_koch[i + 1].y + 0.5), 0);
}
}1.2. Sierpinsk gasket
두 점의 중 점을 찍다보면 안찍히는 부분이 있음.
- 초기 점 3개를 설정
- 점 s를 설정
- 초기 점 3개 중 임의의 점을 선택(랜덤)
- 중점을 계산한 후 그 부분에 점 찍기
- 찍은 점을 다시 s로 설정
- 위 부분 반복

void seirpinskigasket(void) {
int i;
int sx, sy, cx, cy, rd;
//초기점을 설정
point gasket[3] = { {30,300}, {400, 30}, {400, 560} };
//초기점을 Bimage에 찍어줌
for (i = 0; i < 3; i++) {
Bimage[(int)gasket[i].x][(int)gasket[i].y] = 0;
}
초기 점을 sx, sy에 넣어줌
sx = gasket[0].x;
sy = gasket[0].y;
for (i = 0; i < 10000000; i++) {
rd = rand() % 3; //초기 점 3개 중 임의의 점 구하기
//s와 임의의 점 사이의 중앙 부분을 구한다.(0.5더해주는건 반올림)
cx = (int)((double)(sx + gasket[rd].x) / 2.0 + 0.5);
cy = (int)((double)(sy + gasket[rd].y) / 2.0 + 0.5);
//구한 부분에 점을 찍어 준다.
Bimage[cx][cy] = 0;
//구한 부분을 다시 s로 설정
sx = cx;
sy = cy;
}
return;
}1.3. Binary split tree
- 점 두 개를 입력 받아 해당 점을 선으로 그은 위 특정 각도로 더 짧은 부분에 점을 찍음
- 이 과정을 반복
- 랜덤은 적절한 각도와 길이를 랜덤으로 설정해주면 됨
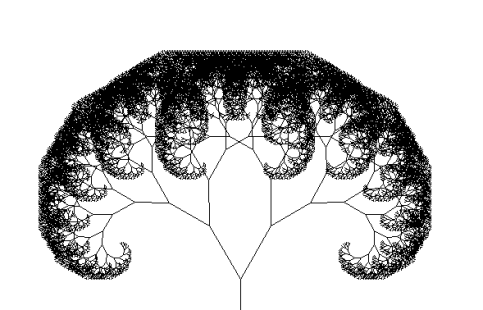
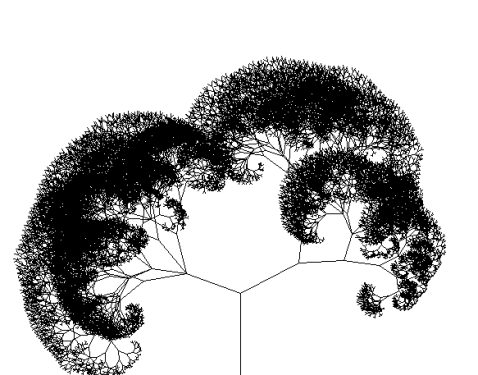
void binaryTree(int x1, int y1, int x2, int y2, int level)
{
int step = level;
double dx, dy, tx, ty;
if (step < 0) {
return;
}
lineDDA(x1, y1, x2, y2, 0);
if (x2 > x1) tx = x2 - abs(x2 - x1) * 0.75; else tx = x2 + abs(x2 - x1) * 0.75;
if (y2 > y1) ty = y2 - abs(y2 - y1) * 0.75; else ty = y2 + abs(y2 - y1) * 0.75;
dx = cos(radian(150)) * (double)(tx - x2) - sin(radian(150)) * (double)(ty - y2) + x2;
dy = sin(radian(150)) * (double)(tx - x2) + cos(radian(150)) * (double)(ty - y2) + y2;
binaryTree(x2, y2, dx, dy, step - 1);
dx = cos(radian(150)) * (double)(tx - x2) + sin(radian(150)) * (double)(ty - y2) + x2;
dy = -sin(radian(150)) * (double)(tx - x2) + cos(radian(150)) * (double)(ty - y2) + y2;
binaryTree(x2, y2, dx, dy, step - 1);
}2. 불변 Fractal
2.1 Mandelbrot
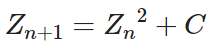
- 복소수 Z를 제곱한 뒤, C를 더해 새로운 Z를 만드는 과정을 반복
- 어떤 C값에서는 Z가 계속 증가하지만 어떤 C값에서는 Z가 아주작은 두 허수 사이를 왕복
- Z의 값이 무한히 발산하지 않는 각각의 C값을 화면 위에 점으로 표현
- openGL로 drawing(mouse로 원하는 부분을 확대가능)

#define CRT_SECURE_NO_WARNINGS
#include <math.h>
#include <gl/glut.h>
#define M 500
#define Z 10
double h = 3., w = 3.;
double cx = -0.0, cy = 0.0;
int init_Flag = 1, m_Flag = 0;
unsigned char image[M][M];
int TLX, TLY, BRX, BRY;
void Mandelbrot(void)
{
double x, y, absolute;
double zx, zy, z2x, z2y;
double m_cx, m_cy;
for (int i = 0; i < M; i++)
{
for (int j = 0; j < M; j++)
{
//scaleing1, scaleing2, translation1, translation2
y = i * (h / (M - 1)) + cy - h / 2;
x = j * (w / (M - 1)) + cx - w / 2;
zx = 0;
zy = 0;
m_cx = x;
m_cy = y;
//발산 확인
for (int k = 0; k < 400; k++)
{
z2x = zx * zx - zy * zy; //정수 부분(i의 제곱은 -1)
z2y = zx * zy * 2; //복소수 부분
zx = z2x + m_cx;
zy = z2y + m_cy;
absolute = zx * zx + zy * zy; //절대값 구할거니 제곱해줌 근데 발산만 검사하면 되니 루트는 안씌어줘도 됨
if (absolute > 4.) break;
}
if (absolute > 4.) absolute = 1.;
image[i][j] = (unsigned char)(absolute * 255.);
}
}
}
void Display(void)
{
int i, j;
glClearColor(1.0, 1.0, 1.0, 1.0);
if (init_Flag == 1)
{
glClear(GL_COLOR_BUFFER_BIT);
Mandelbrot();
}
init_Flag = 0;
glBegin(GL_POINTS);
for (i = 0; i < M; i++)
{
for (j = 0; j < M; j++)
{
glColor3ub(image[i][j], image[i][j], image[i][j]);
glVertex3i(j, i, 0);
}
}
glEnd();
if (m_Flag == 1)
{
glBegin(GL_LINE_LOOP);
glColor4f(1.0, 0.0, 0.0, 0.0);
glVertex3i(TLX, M - TLY, Z);
glVertex3i(TLX, M - BRY, Z);
glVertex3i(BRX, M - BRY, Z);
glVertex3i(BRX, M - TLY, Z);
glEnd();
}
glutSwapBuffers();
}
void Reshape(int w, int h)
{
glViewport(0, 0, w, h);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(M / 2., M / 2.0f, M / 2.0f,
M / 2.0f, M / 2.0f, 0.0f,
0.0f, 1.0f, 0.0f);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(-250.0, 250.0, -250.0, 250.0, 100.0, 1000.0);
}
void MouseMove(GLint x, GLint y)
{
BRX = x;
BRY = y;
glutPostRedisplay();
}
void MouseClick(GLint Button, GLint State, GLint x, GLint y)
{
int px, py;
int wideW;
if (Button == GLUT_LEFT_BUTTON && State == GLUT_DOWN)
{
TLX = x;
TLY = y;
m_Flag = 1;
}
if (Button == GLUT_LEFT_BUTTON && State == GLUT_UP)
{
BRX = x;
BRY = y;
px = (TLX + BRX) / 2; py = (TLY + BRY) / 2;
if (abs(BRX - TLX) > abs(BRY - TLY))
{
wideW = abs(BRX - TLX);
}
else
{
wideW = abs(BRY - TLY);
}
cx += (px - M / 2) * w / M; cy -= (py - M / 2) * h / M;
h = w = wideW * h / M;
init_Flag = 1;
m_Flag = 0;
Display();
}
}
void MyInit()
{
glShadeModel(GL_SMOOTH);
}
int main(int argc, char** argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_RGBA | GL_DOUBLE);
glutInitWindowSize(M, M);
glutCreateWindow("openGL");
glutReshapeFunc(Reshape);
glutMotionFunc(MouseMove);
glutMouseFunc(MouseClick);
glutDisplayFunc(Display);
glutMainLoop();
}