최소 신장 트리(Minimum Spanning Tree)
주어진 가중치 그래프에서 사이클이 없이 모든 점들을 연결시킨 트리 중에서 간선들의 가중치 합이 최소인 트리
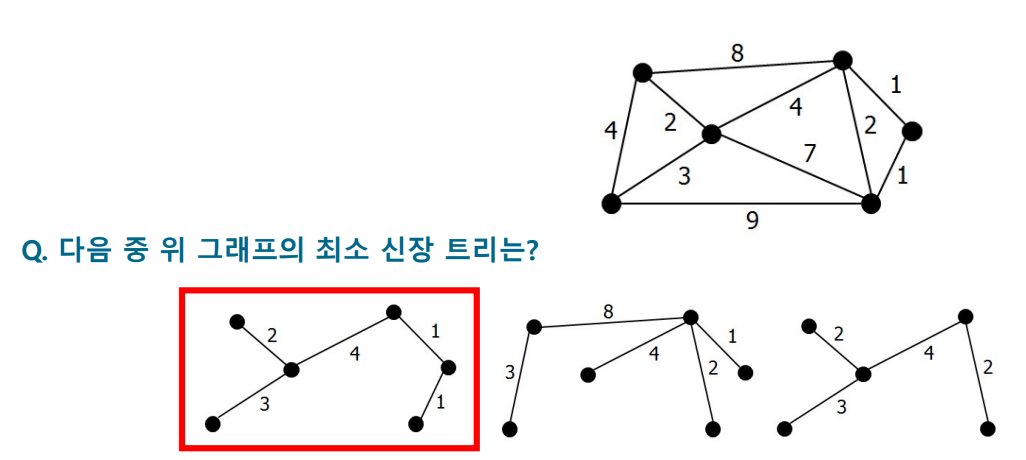
- 주어진 그래프의 신장 트리를 찾는 법
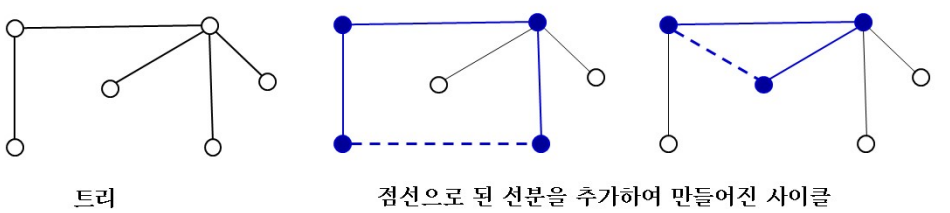
- 사이클이 발생하지 않도록 모든 정점을 연결
- 그래프 내의 정점의 수 = n
- 신장 트리에는 정확히 (n-1)개의 간선이 존재
- 트리에는 간선을 하나 추가시키면 반드시 사이클이 생성 됨
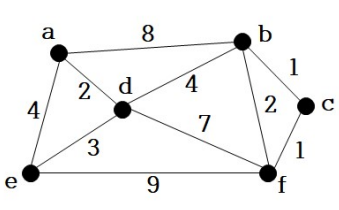
Kruskal의 MST 알고리즘
- 최소 신장 트리가 최소 비용의 간선으로 구성됨과 동시에 사이클을 포함하지 않는다는 조건에 근거하여 고안된 알고리즘
- 각 단계에서 사이클을 이루지 않는 최소 가중치를 갖는 간선을 선택
- Kruskal 알고리즘의 MST 구축 순서
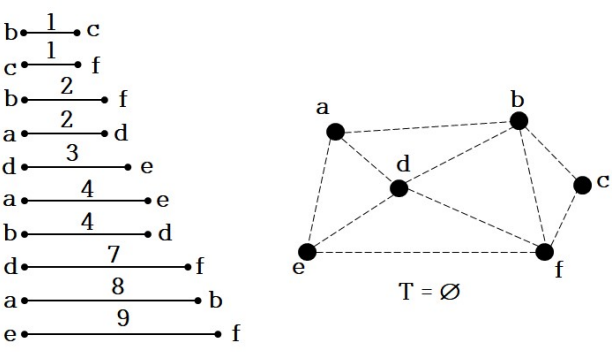
- 그래프 내의 모든 간선들을 가중치에 따라 오름차순으로 정렬
- 정렬된 간선들의 리스트에서 맨 앞에 위치한 간선을 선택
- 선택한 간선이 사이클을 생성하는지 확인한 후 사이클을 생성하지 않으면 해당 간선을 그래프에 추가
- 선택한 간선이 사이클을 생성하는 겨우 그 간선은 제외후 간선 선택을 반복
1. 수행과정 예시
-
해당 간선을 길이에 따라 정렬
-
길이가 작은 간선부터 선택하여 추가
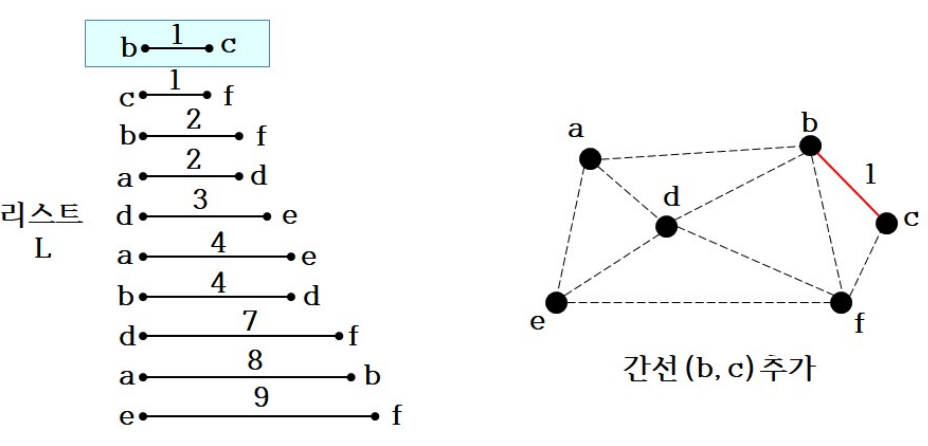
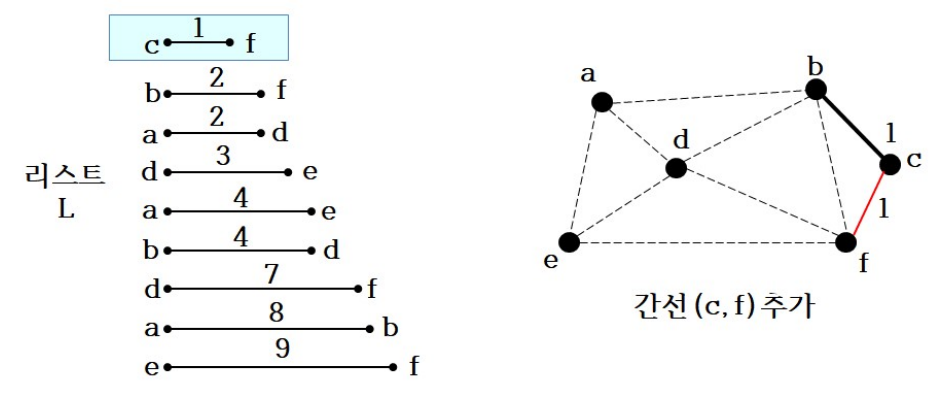
-
사이클이 나오는 경우 간선을 버림
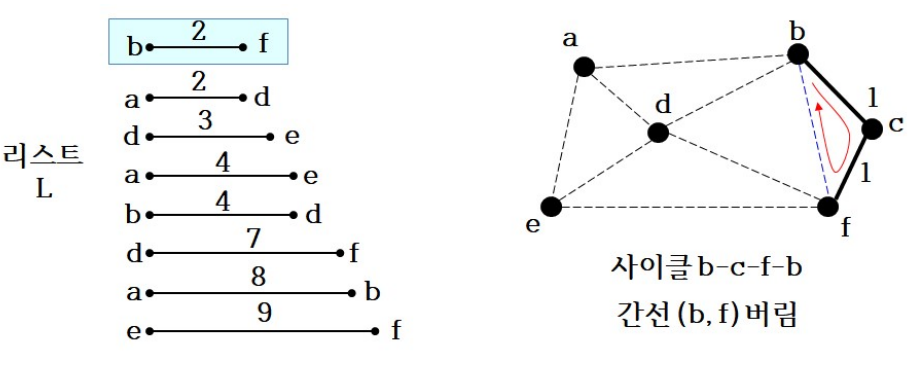
-
다시 간선 선택 반복
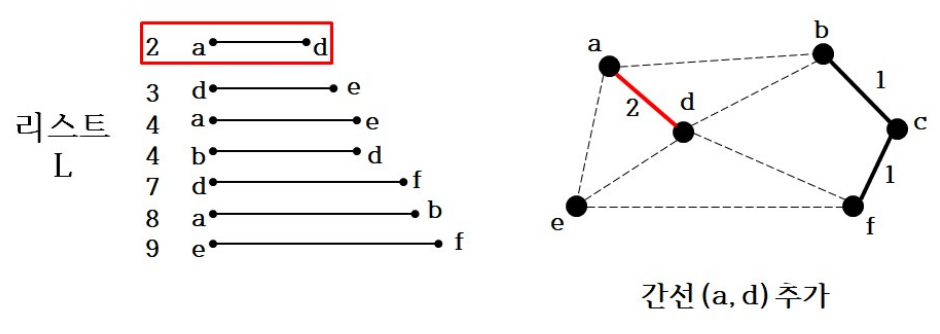
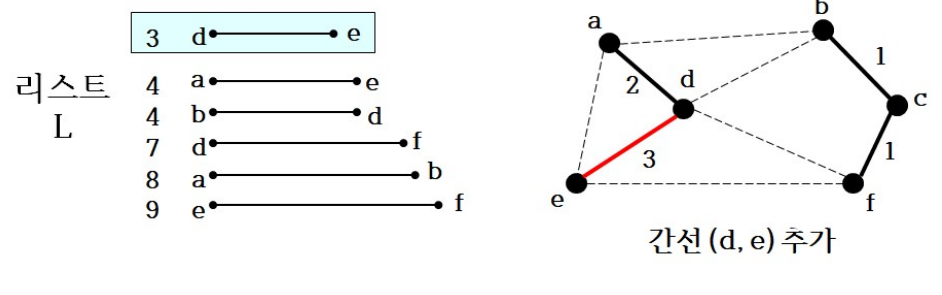
-
사이클 발생!->버림
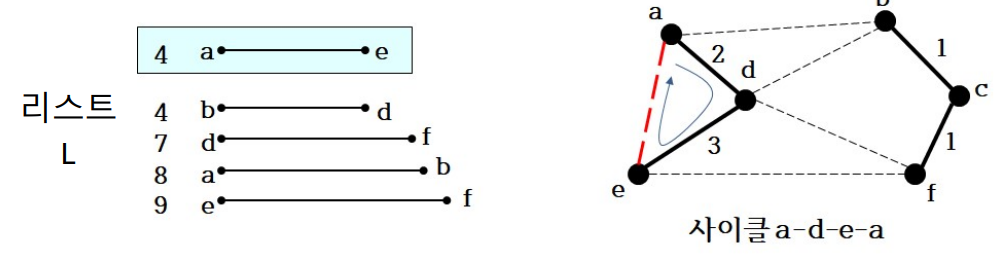
-
다시 간선 선택
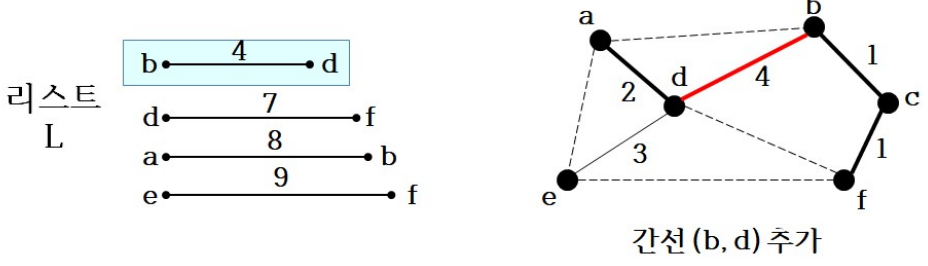
-
최종 MST
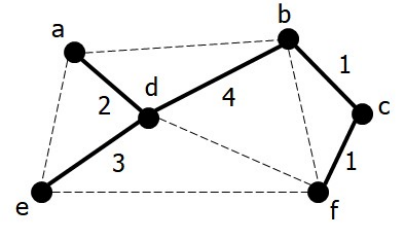
2. 사이클 발생 여부 확인법
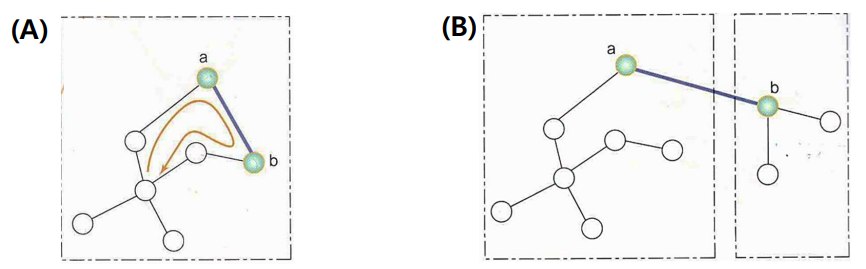
- (A) 간선의 양 끝 정점 모두 같은 집합에 속하면 해당 간선을 추가했을 때 사이클이 형성
- (B) 간선이 양 끝 정점이 서로 다른 집합에 속하는 경우 해당 간선을 추가해도 사이클이 형성되지 않음
- 이를 효과적으로 수행하기 위해 Union-find연산
3. Union-Find
3.1. 분리 집합의 표현방법
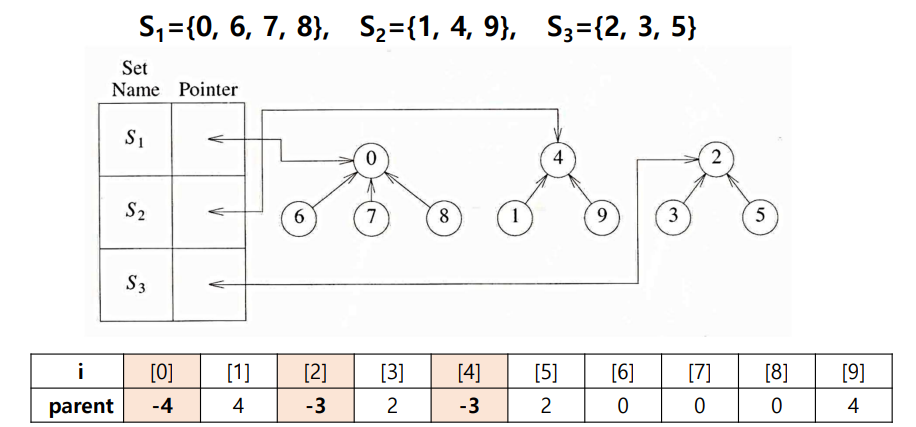
- 분리 집합은 서로 어떤 원소도 공통으로 가지지 않는 두 개 이상의 깁합을 의미하며, 이들은 각각의 집합은 트리로 표현 가능
- 각 집합은 해당 집합을 나타내는 트리의 루트 노드 값으로 구분
- S_1 = {0,6,7,8}, S_2 = {1,4,9}, S_3 = {2,3,5}
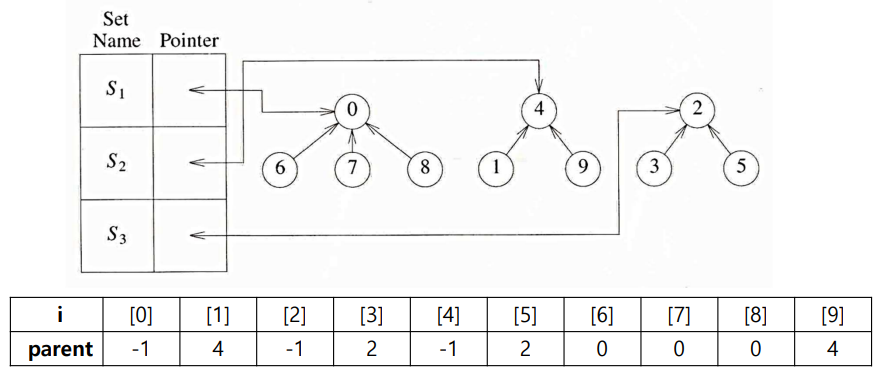
3.2. Union 연산
- union(i,j): 두 집합 S_i, S_j의 합집합을 만듦
- 해당 집합을 나타내는 두 트리 중에서 하나를 선택하여 다른 트리의 서브 트리로 만듦
- 예) S1과 S2에 대한 합집합 S1US2의 표현방법
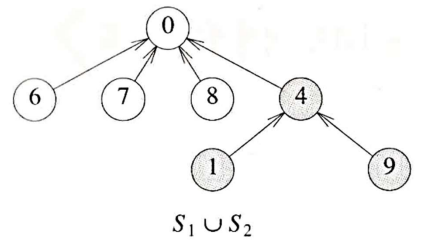
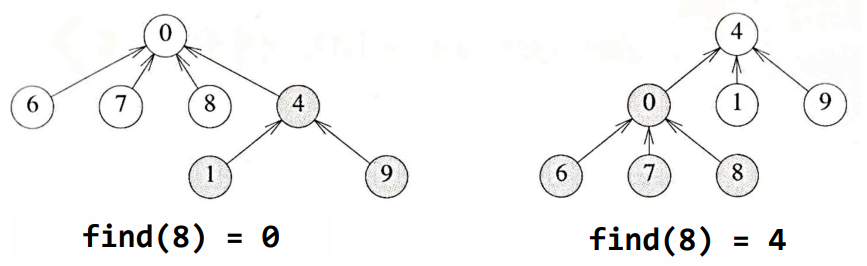
3.3. Find 연산
-
find(i): 원소 i를 포함하는 집합을 탐색하고, 해당 집합에 해당하는 트리의 루트 노드를 반환
- 예) S_1 U S_2에서 원소8에 대한 find(8)의 수행결과
3.4. 간단한 Union-Find 연산의 문제점
- 아래의 Union-Find연산을 연속적으로 수행하면 트리의 층이 n개가 되어버림
- 이러한 선형 구조의 트리를 변질트리라 부름
- 변질 트리에서 (n-1)의 find를 수행하는데 소요시간: O(n^2)

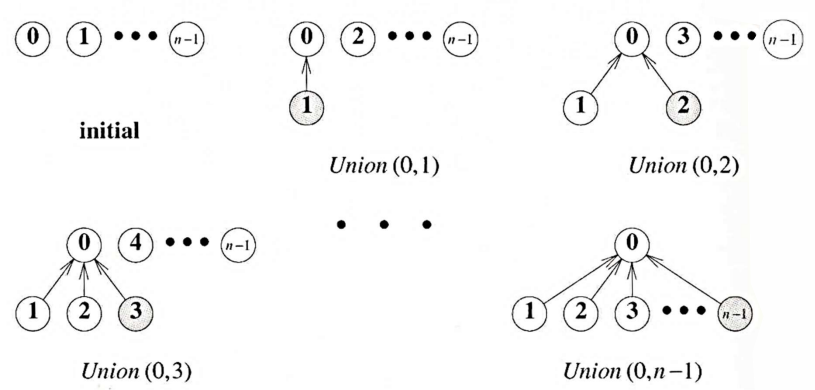
3.5. 가중 규칙을 적용하여 Union 연산 개선
- Union(i, j)를 위한 가중 규칙
- 루트 노드 i를 가진 트리의 노드 수가 루트 노드 j를 가진 트리의 노드 수보다 적으면 노드 j를 노드 i의 부모로 만들고, 그렇지 않으면 노드 i를 노드 j의 부모로 만듦
- 이를 위해 parent 배열에서 루트 노드에 해당하는 값은 해당 트리가 포함하는 원소의 총 개수를 음수로 표현하여 저장함
- 예제
3.6. 붕괴 규칙을 적용한 find연산
- find(i)의 붕괴규칙
- 만일 노드 j가 노드i에서 루트로 가는 경로상에 있으면서 parent[i] != root(i)이면, parent[j]를 root[i]로 지정
- 붕괴 규칙의 역할
- find(i) 연산 수행시 find 연산의 목표가 되는 노드 i의 부모 노드를 루트 노드의 자식 노드로 지정
- 해당 작업을 i부터 루트 노드까지의 경로상에 있는 모든 노드에 대하여 반복적 수행
- 이에 따라 트리의 높이를 낮춤으로써 변질 트리가 되는 현상을 방지 가능
소스 코드
#include <iostream>
#include <vector>
#include <algorithm>
#define Max 1001
using namespace std;
int parents[Max];
class Edge {
public:
int node[2];
int distance;
Edge(int a, int b, int dis)
{
this->node[0] = a;
this->node[1] = b;
this->distance = dis;
}
bool operator<(Edge& edge)
{
return this->distance < edge.distance;
}
};
int findParent(int node)
{
if (parents[node] < 0) return node;
return parents[node] = findParent(parents[node]);
}
void unionParent(int a, int b)
{
a = findParent(a);
b = findParent(b);
if (parents[a] <= parents[b]) // a가 밑으로 들어감
{
parents[b] += parents[a];
parents[a] = b;
}
else
{
parents[a] += parents[b];
parents[b] = a;
}
}
bool isCycle(int a, int b)
{
a = findParent(a);
b = findParent(b);
if (a == b) return true;
else return false;
}
int main()
{
vector<Edge> v;
v.push_back(Edge(0, 1, 10));
v.push_back(Edge(0, 2, 5));
v.push_back(Edge(1, 2, 7));
v.push_back(Edge(1, 3, 4));
v.push_back(Edge(2, 3, 3));
v.push_back(Edge(2, 4, 2));
v.push_back(Edge(3, 4, 1));
//간선 가중치 기준 오름차순 정렬
sort(v.begin(), v.end());
//부모노드 초기화
memset(parents, -1, sizeof(parents));
int sum = 0; // 간선의 가중치 합
for (int i = 0; i < v.size(); ++i) {
//싸이클 여부 확인
if (!isCycle(v[i].node[0], v[i].node[1])) {
sum += v[i].distance;
unionParent(v[i].node[0], v[i].node[1]);
}
}
// 최소 신장 트리 가중치 합 출력
cout << sum;
return 0;
}