Prim 알고리즘
- 시작 정점에서 출발하여 신장 트리 집합을 단계적으로 확장해나가는 방법
- Kruskal 알고리즘과 달리 그래프의 정점을 추가하는 과정을 통해 최소 신장트리를 구축
- Prim 알고리즘의 MST 구축 순서
- 시작 단계에서는 시작 정점만이 신장 트리 집합에 포함
- 앞 단계에서 만들어진 신장 트리 집합에, 인접한 정점들 중에서 최저 가중치 간선으로 연결된 정점을 선택하여 트리를 확장
- 이 과정을 트리가 (n-1)개의 간선을 가질 때까지 계속 반복
1. 알고리즘 수행 과정
-
임의의 정점 c를 선택하고 D[c] = 0으로 초기화
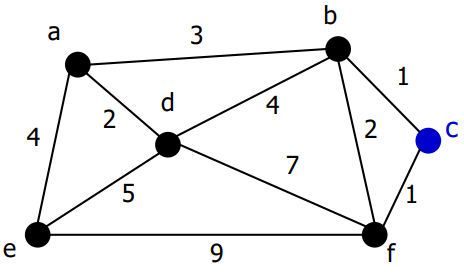

-
시작 정점 c와 간선으로 연결된 각 정점 v에 대해서, D[v]를 각 간선의 가중치로 초기화
-
나머지 각 정점 v에 대해서, D[v]를 ∞로 초기화
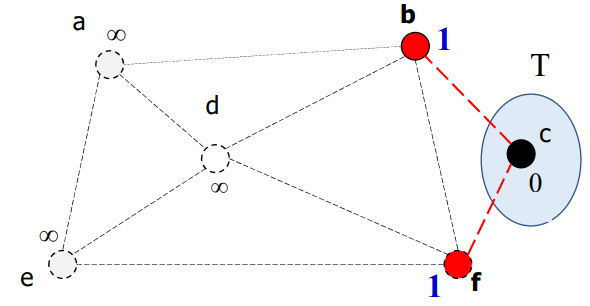

-
T = {c}로 초기화
-
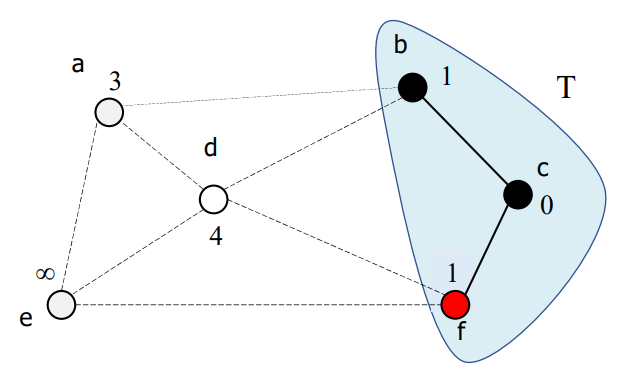
T에 가장 가까운 정점 b를 추가
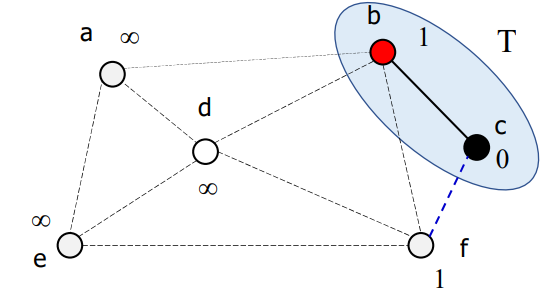

-
정점 b에 연결된 정점 a와 d에 대한 거리 D[a]와 D[d] 갱신
-
한편, 정점 f에 대해서는 정점 b와 연결되어 있음에도 불구하고, D[f]를 갱신하지 않음
- 원래 가중치가 더 작기 때문
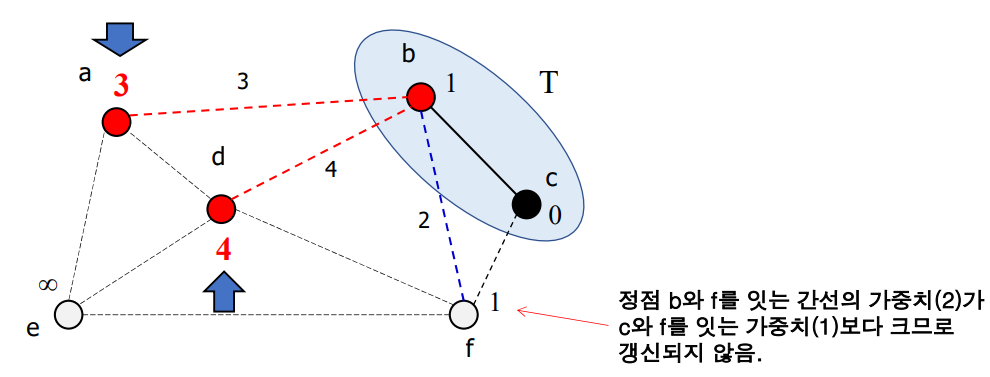

- 원래 가중치가 더 작기 때문
-
T 에 가장 가까운 정점 f를 추가
-
해당 과정을 정점을 (n-1)개의 간선을 가질 때 까지 반복(모든 정점이 추가될 때 까지)
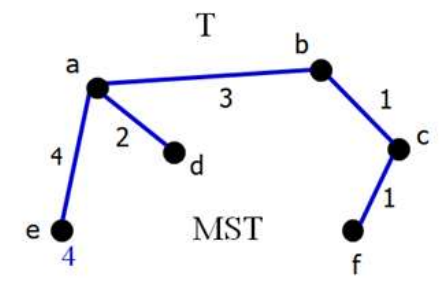
2. 사이클이 없는 Prim
- PrimMST가 찾은 T에는 왜 사이클이 없을까?
- Prim은 집합 T밖에 있는 점을 항상 추가하기 때문에 사이클이 만들어지지 않음
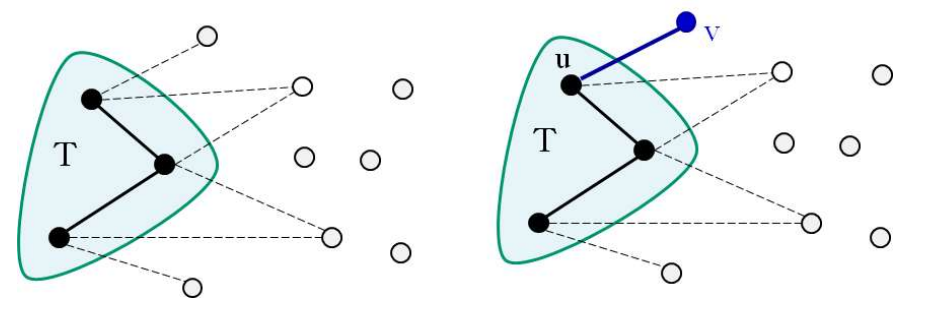
- Prim은 집합 T밖에 있는 점을 항상 추가하기 때문에 사이클이 만들어지지 않음
3. 시간복잡도
- While-루프가 (n-1)회 반복:
- 1회 반복될 때 T에 속하지 않은 정점 중 최소인 점을 찾는데 O(n)이 걸림
- 이는 배열 D에서 최소값을 찾는것이고, 배열의 크기는 n이기 때문
- Prim 시간복잡도
- while 문에서 소요되는 시간: (n-1) * O(n) = O(n^2)
- 최소 힙을 사용하면 O(mlongn) (m은 간선의 수)
- 따라서 간선의 수가 O(n)이면, 총 시간복잡도는 O(nlogn)
4. 크루스칼 알고리즘과 비교
- Kruskal Algorithm
- 간선이 1개씩 T에 추가되는데, 이는 마치 n개의 점들이 각각의 트리인 상태에서 간선이 추가되면 2개의 트리가 1개의 트리로 합쳐지는 것이라 생각하면 됨
- Kruskal 알고리즘은 이를 반복하여 1개의 트리인 T를 생성
- n개의 트리들이 점차 합쳐지면서 1개의 신장트리가 완성
- Prim 알고리즘
- T가 점 1개의 트리에서 시작되어 간선을 1개씩 추가
- 1개의 트리가 점차적으로 자라나면서 신장트리가 완성
