백트래킹(Backtracking)

• 해를 탐색하는 도중 막히면 되돌아가서 다시 해를 탐색
  -최적화(optimization)문제와 결정(decision)문제를 해결하는 데 유용하게 활용
  • 결정(decision)문제: 문제의 조건을 만족하는 해가 존재하는 지의 여부를 yes 또는 no로 답

---

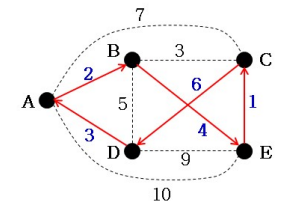
여행자 문제(Traveling Salesperson Problem, TSP)

1. Algorithm

tour = [시작 노드] // tour는 노드의 순서를 저장하는 리스트 변수
bestSolution = (tour, ∞)
Algorithm BacktrackTSP(tour)
1. If tour가 완전한 해인 경우
2. If tour의 거리 < bestSolution의 거리
3. bestSolution = <tour, tour의 거리>
4. else 
5. for tour에 포함된 노드를 확장 가능한 각 노드 v에 대해서
6. newTour = append(tour, v) // 리스트 변수 “tour” 뒤에 노드 v 를 추가(append)
7. if newTour의 거리 < bestSolution의 거리
8. BacktrackTSP(newTour)

2. 수행과정

2.1. 시작

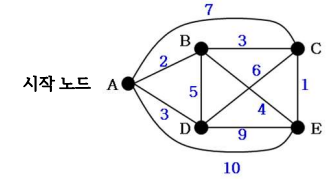
• 시작 노드: A, tour=[A], bestSolution=([A],∞)
  • BacktrackTSP(tour)를 호출

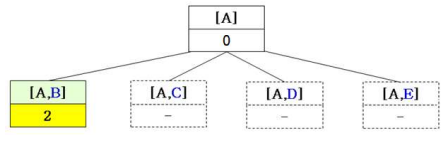
2.2. BacktrackTSP([A, B])

• tour[A]를 확장할 수 있는 노드는 B, C, D, E
  • 각 노드에 대해 반복문을 수행
• 먼저 B에 대해 newTour = [A,B]이고 newTour의 거리 = 2
  

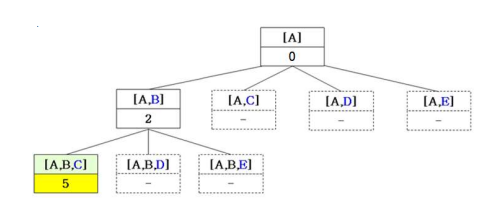
2.3. BacktrackTSP([A, B, C])

• tour[A, B]를 확장할 수 있는 노드는 C, D, E
  • 각 노드에 대해 반복문을 수행
• 먼저 C에 대해 newTour = [A,B,C]이고 newTour의 거리 = 5
  

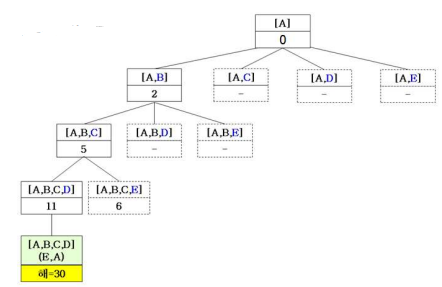
2.4. bestSolution=([A, B, C, D, E, A], 30)

• 종료조건까지 반복해 [A, B, C, D, E, A]를 탐색 가능
  

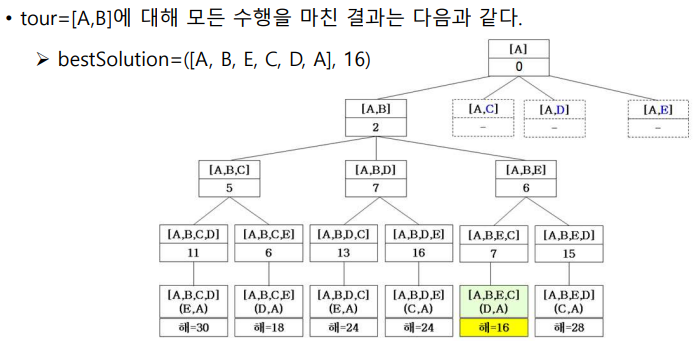
2.5. tour=[A, B]

2.6. tour=[A, C]

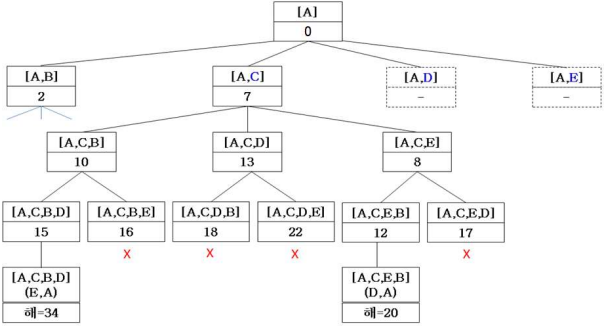
• x로 표시된 4개의 상태 각각은 bestSolution의 거리보다 짧지 않으므로 더 이상 탐색되지 않고, 가지치기(pruning)

2.7. 수행결과

• 최종해는 [A, B, E, C, D, A], 거리는 16
  

3. 시간복잡도

• Backtracking 알고리즘의 시간 복잡도는 상태 공간 트리의 노드 수에 비례
• n개의 노드로 구성된 그래프에 대해서 BacktrackTSP 알고리즘이 탐색하는 최대 크기의 상태 공간 트리
  
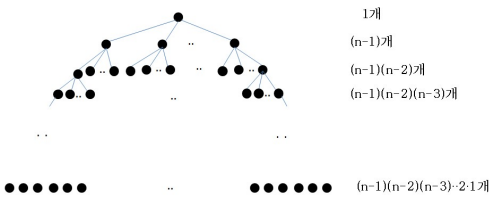
• 위의 트리의 단말 노드 수만 계산해도 (n-1)!