휴리스틱 알고리즘

불충분한 시간이나 정보로 인하여 합리적인 판단을 할 수 없거나, 체계적이면서 합리적인 판단이 굳이 필요하지 않은 상황에서 사람들이 빠르게 사용할 수 있게 보다 용이하게 구성된 간편 추론의 방법

기본적으로 모두 최적해가 될 가능성이 없는 답들을 탐색하는 것을 방지해 탐색할 답의 수를 줄이는 것을 목표로 함

휴리스틱 관련 이론

• 가지치기(pruning)기법
• Simulated Annealing(담금질 기법)
• Genetic Algorithms (유전 알고리즘)

1. 가지치기(pruning)기법

• 탐색 과정에서 최적해로 연결될 가능성이 없는 부분들을 잘라냄
  • 존재하는 답 중 일부는 아예 탐색하지 않기 때문에 프로그램의 동작 속도가 빨라짐
  • 효율성을 극대화하기 위해 가장 좋은 답의 상한을 빨리 찾아내서 탐색을 초기에 종료해야 함
    - 분기한정 사용 가능

    예를 들어 길이가 10인 경로를 이미 찾았는데, 이후 다른 경우의 수를 구하는 과정에서 도착점에 도착하기도 전에 길이가 10이 넘어가면 마저 탐색하지 않고 종료해버린다.

2. 유전 알고리즘

• 자연계의 진화 체계를 모방한 메타휴리스틱 알고리즘으로 복잡한 최적화 문제를 푸는데 사용됨
  • 찰스 다윈의 진화론으로부터 창안된 해 탐색 알고리즘으로 적자생존의 개념을 생각하면 됨
• 스케줄링 등 복잡한 최적화 문제를 해결하는데 활용되며, 딥러닝의 초기 웨이트 설정, 특징 선택 등 머신러닝 문제를 해결하는데 사용됨

2.1. 최적화 문제

• 제약 하에서 목적식을 최소화 혹은 최대화하는 결정 변수의 값을 찾는 문제
• 제약: 해가 만족해야 하는 조건
• 목적식: 최소화 혹은 최대화해야 하는 대상이며
• 결정 변수: 값을 찾아야 하는 변수

2.2. 유전 알고리즘 개념

• 여러 개의 해로 구성된 해 집단을 만들고 평가한 뒤, 좋은 해를 선별해 새로운 해 집단을 만드는 메타휴리스틱 알고리즘
• sudo 코드

1. 초기 후보해 집합 G0을 생성
2. G0의 각 후보해를 평가
3. t = 0
4. do
5.   Gt로부터 Gt+1을 생성
6.   Gt+1의 각 후보해를 평가
7.   t = t+1
8. while(종료조건이 만족될 때 까지)
9. return Gt의 후보해 중 가장 우수한 해

• 알고리즘의 주요부분
  현재 세대의 후보해에 대해서 다음과 같은 3개의 연산을 통해 다음 세대의 후보를 생성
  • 선택(selection)연산
  • 교차(crossover)연산
  • 돌연변이(mutation)연산

2.3. 선택연산

현재 세대의 후보해 중 우수한 후보해를 선택하는 연산

현재 세대에 n개의 후보해가 있다면, 이들 중 우수한 후보해는 중복되어 선택될 수 있고, 적합도가 상대적으로 낮은 후보해들은 선택되지 않을 수도 있다. 이렇게 선택된 후보해의 수는 n개로 유지된다. 이러한 선택은 적자생족 개념을 모방한 것이다.

• 구현
  가장 간단히 구현하는 룰렛 휠(.roulette wheel) 방법: 돌려돌려 돌림판을 생각하자

  후보해1의 적합도가 10, 후보해2의 적합도가 5, 후보해3의 적합도가 3, 후보해4의 적합도가 2라고 하자. 이때 후보해가 차지하는 돌림판의 면적은 (후보해 적합도/모든 후보해의 적합도의 합)이 된다. 모든 면적은 20, 후보해1의 면적은 10/20 = 50%, 후보해2의 면적은 5/20 = 25%, 후보해3의 면적은 3/20 = 15%, 후보해4의 면적은 2/20 = 10%이다. 현재 4개의 후보해가 있으므로, 4개의 원판을 돌리고 회전이 멈추었을 때 핀이 가ㄹ키는 후보해를 각각 선택하면 된다.

2.4. 교차 연산

선택 연산을 수행한 후의 후보해 사의에 수행되는 방법으로, 염색체가 교차하는 것을 그대로 모방한 것

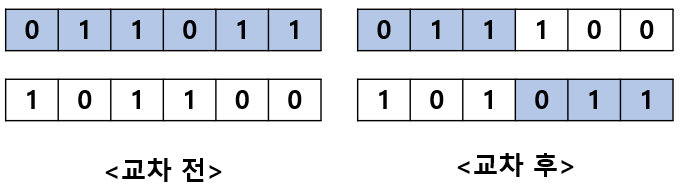
2개의 후보해가 각각 2진수로 표현된다면, 교차점 이후의 부분을 서로 교환하여 교차연산을 수행하고 그 결과로 각각 새로운 후보해가 만들어 짐. 이와 같은 교차 연산을 1-점(point)교차 연산이라고 함
후보해가 길게 표현되면, 여러 개의 교차점을 임의로 정하여 교차 연산을 할 수 도 있다. 선택 연산을 통해서 얻은 수보다 우수한 후보해를 생성하는 것이 목적이다. 문제에 따라 교차 연산을 수행할 후보해의 수를 조정하는데, 이를 교차율이라고 한다. 일반적으로 교차율은 0.2~1.0 범위에서 정한다.

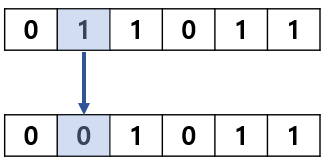
2.5. 돌연변이 연산

교차 연산 후에 수행되는 연산으로 아주 작은 확률로 후보해의 일부분을 임의로 변형시키는 것이다. 이 확률을 돌연변이율(mutation rate)이라고 하며, 일반적으로(1/PopSize)~(1/Length)의 범위에서 사용된다.

• PopSize: 모집단 크기로, 한 세대의 후보해의 수
• Length: 후보해를 이진 표현으로 했을 경우의 bit 수