최근접점의 쌍 찾기
- 2차원 평면 상의 n개의 점이 입력으로 주어질 때,거리가 가장 가가운 한 쌍의 점을 찾는 문제
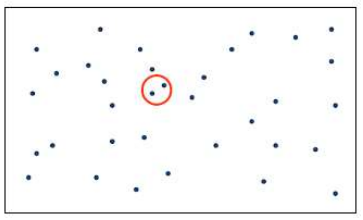
1. 간단한 방법
- 모든 두 점의 거리를 계산
- 시간복잡도
- nC2 = n(n-1)/2 = O(n^2)
- 한쌍의 거리계산: O(1)
- O(1)*O(n^2) = O(n^2)
2. 효율적인 분할 방법
- n개의 점을 1/2개로 분할하여 각 부분문제에서 최근접 점의 쌍을 찾음
- 그 다음에, 2개의 부분 해 중에서 짧은 거리를 가진 점의 쌍을 찾음
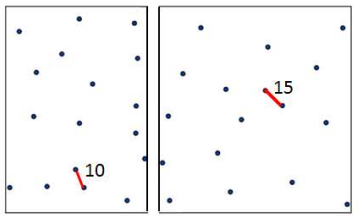
- 두 부분 문제를 하나로 취합시 중간 영역을 고려해야 함
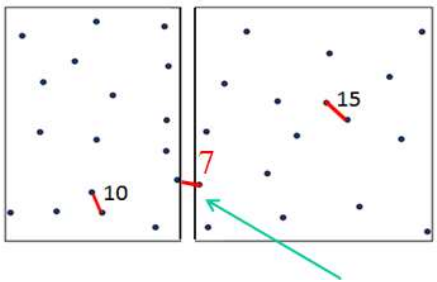
3. 중간 영역 안의 점들
- 최근접 쌍의 거리인 d이내의 중간 영역 안에 포함된 점들 중 거리가 더욱 짧은 근접 쌍이 존재하는지 확인
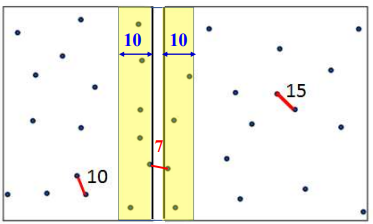
4. 중간 영역에 있는 점 찾기
- d = min(왼쪽 부분의 최근접 점의 상 사이 거리, 오른쪽 부분의 최근접 점의 상 사이 거리)
- 각각의 점은 1차원 배열 내에 x좌표의 오름차순으로 정렬되어 저장
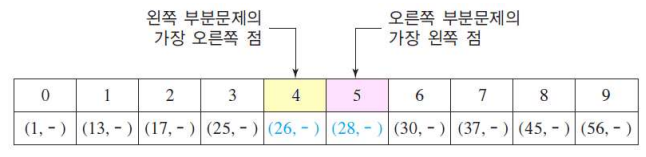
- 중간 영역에 속한 점 = (왼쪽 부분 문제에서 가장 오른쪽 점의 x좌표에서 d를 뺀 값과 오른쪽 부분 문제에서 가장 왼쪽 점의 x좌표에 d를 더한 값 사이의 x좌표 값을 가진 모든점)
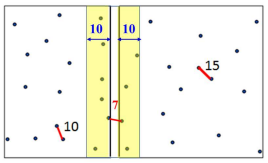
- d=10,(25,-),(26,-),(28,-),(30,-),(37,-)
- 2차원 좌표상의 점들을 표현하기 위한 자료구조

- 알고리즘
ClosetsetPair(S):
if(|S|<=3) return (2 또는 3개의 점들 중 거리가 가장 짧은 쌍)
정렬된 S를 같은 길이의 SL과 SR로 분할한다.
CPL = ClosestPair(SL)
CPR = ClosestPair(SR)
d = min{ dist(CPL), dist(CPR) }
CP_C = 중간 영역에 속하는 최근접 점의 쌍
return (CPL, CPC, CPR 중 거리가 가장 짧은 쌍)5. 알고리즘 수행 과정
- ClosestPair(S) 호출
- S를 SL과 S_R로 분할

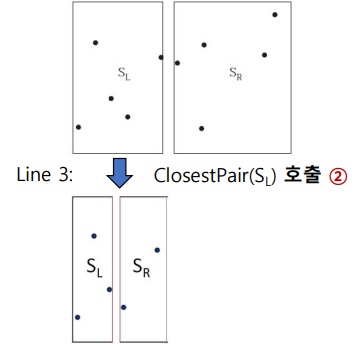
- S를 SL과 S_R로 분할
- 중간영역에서 CPc를 찾기

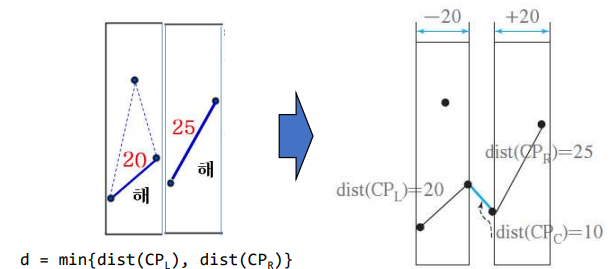
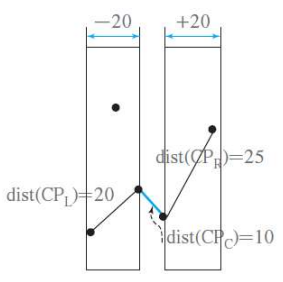
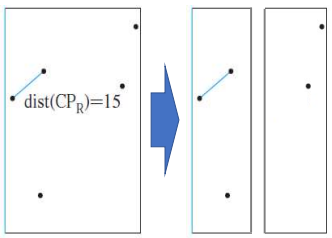
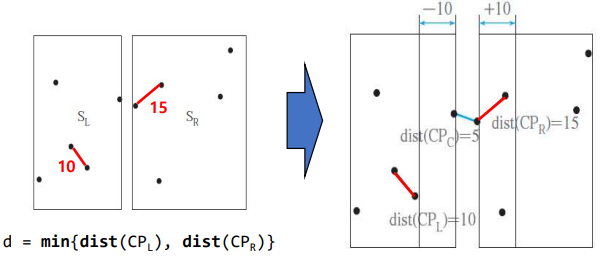
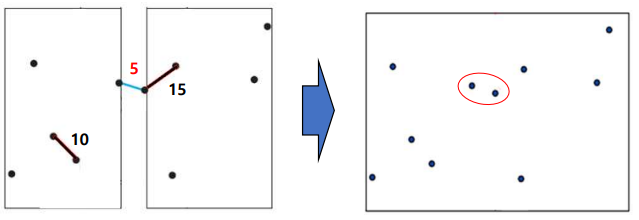
- 알고리즘 수행 과정에서 분할정복 개념
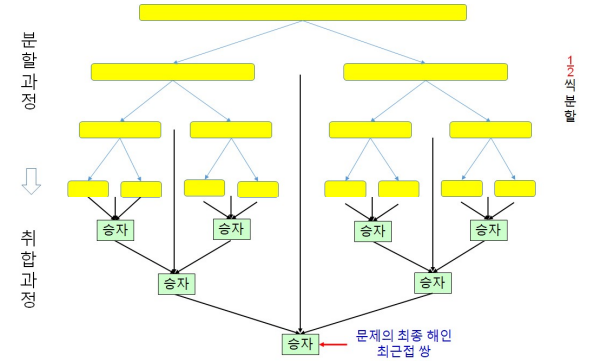
6. 알고리즘 분석
- 배열 S에 총 n개의 점이 있으면 전처리 과정으로서 S의 점을 x좌표를 기준으로 정렬 수행:
O(nlogn) - 배열 S에 3개의 점이 있는 경우 총 3번의 거리계산이 필요하고, S내의 점 수가 2이면, 1번의 거리 계산이 필요:
O(1) - S_L, S_R에 대하여 각각 ClosestPair를 순환 호출하여 반복적으로 분할을 수행
- d = min(dist(CP_L), dist(CP_R))일 때 중간 영역에 속하는 점들 중에서 최근접점의 쌍을 찾음
- 이를 위해 중간 영역에 있는 점을 y좌표 기준으로 정렬후, 아래에서 위로 각 점을 기준으로 거리가 d이내인 주변의 점들 사이의 거리를 계산해 중간거리의 최근접 점의 쌍을 찾음
- y좌표로 정렬 O(nlogn)의 시간이 걸리고, 아래에서 위로 올라가며 각 점에서 주변의 점들 사이의 거리를 계산하는데 O(1) 시간이 소요됨(각 점과 거리를 계산해야 하는 이웃 점들의 수가 O(1)이기 때문)
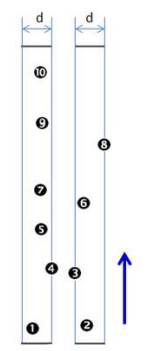
- 3개의 점의 쌍 중에 가장 거리가 짧은 점의 쌍을 리턴:
O(1) - k층까지 분할 된 뒤 정복과정을 수행
- 각 층에서의 수행 시간: O(nlogn)
- 층의 개수: O(logn)
- O(nlogn)*O(logn) = O(nlog^2n)
의견
2차원 평면상에서 일어나는 일이기 때문에 고려해야 될 요소가 x,y 두 가지라는 점에서 어려움을 겪을 수 있다. 언제 x좌표를 고려해 sort하고, 언제 y좌표를 고려해 sort하는지 생각하는것이 중요하다.
소스코드
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
using namespace std;
const int MAX = 2000000000;
int N;
vector<pair<int, int>> arr;
// low번째 점과 high번째 점 사이 거리를 구한다
int Distance(int low, int high){
int lowX = arr[low].first, lowY = arr[low].second;
int highX = arr[high].first, highY = arr[high].second;
int disX = highX - lowX, disY = highY - lowY;
return disX * disX + disY * disY;
}
// 가장 가까운 두 점의 거리를 구하는 재귀함수를 이분 탐색을 통해 구현한다
int BinarySearch(int low, int high){
// 기저 조건은 처음과 끝 숫자의 차이가 1인 경우다
if(low == high)
return MAX;
if(low + 1 >= high)
return Distance(low, high);
int disMin = Distance(low, high);
int tempDis = 0, mid = (low + high) / 2;
// 왼쪽 영역의 최소 거리를 구하고
if((tempDis = BinarySearch(low, mid)) < disMin){
disMin = tempDis;
}
// 오른쪽 영역의 최소 거리를 구하여 둘 중 최솟값을 찾는다
if((tempDis = BinarySearch(mid + 1, high)) < disMin){
disMin = tempDis;
}
vector<pair<int, int>> inner;
// 중간 영역에서 기준선과 x값의 차이의 제곱이 최솟값 이하인 영역의 점들을 찾는다
int lineX = arr[mid].first;
// 왼쪽 영역
for(int i=mid; i>=low; i--){
int x = arr[i].first, dist = lineX - x;
if(disMin <= dist * dist) break;
inner.push_back({arr[i].second, arr[i].first});
}
// 오른쪽 영역
for(int i=mid+1; i<=high; i++){
int x = arr[i].first, dist = lineX - x;
if(disMin <= dist * dist) break;
inner.push_back({arr[i].second, arr[i].first});
}
int len = inner.size();
// 아무 점도 못찾았으면 최솟값을 반환한다
if(len == 0) return disMin;
// y값에 대해 정렬한다
sort(inner.begin(), inner.end());
for(int i=0; i<len; i++){
int iX = inner[i].second, iY = inner[i].first;
for(int j=i+1; j<len; j++){
int jX = inner[j].second, jY = inner[j].first;
int distX = jX - iX, distY = jY - iY;
// 두 점의 y좌표의 차이를 제곱한 값이 최솟값 이상이면 loop를 멈춘다
if(disMin <= distY * distY) break;
// 두 점의 x좌표의 차이를 제곱한 값이 최솟값 이상이면 건너뛴다
if(disMin <= distX * distX) continue;
int dist = distX*distX + distY*distY;
if(dist < disMin)
disMin = dist;
}
}
return disMin;
}
int main(){
scanf("%d",&N);
arr = vector<pair<int, int>>(N);
for(int i=0; i<N; i++){
scanf("%d %d", &arr[i].first, &arr[i].second);
}
sort(arr.begin(), arr.end());
printf("%d \n", BinarySearch(0, N-1));
}