선택 문제
- n개의 숫자들 중에서 k번째로 작은 숫자를 찾는 문제
- k번째로 작은 숫자를 찾는 간단한 방법
- 방법1: 최소 숫자를 k번 찾기
O(kn) - 방법2: 숫자들을 정렬한 후, k번째 숫자 찾기
O(nlogn)
- 방법1: 최소 숫자를 k번 찾기
- 이 문제도 탐색 문제의 일종으로 이진탐색을 사용 가능
- 정렬된 리스트에서 중간에 위치한 숫자와 탐색하는 숫자를 비교한 후, 리스트를 절반으로 나눠 오른쪽 또는 왼쪽부분 리스트만 탐색
1. 선택 문제 아이디어
- Small group은 피봇보다 작은 숫자의 그룹이고, Large group은 피봇보다 큰 숫자의 그룹
- 이렇게 분할했을 때 알아야할 것은 각 그룹의 크기
- 크기를 알면 k번째로 작은 수가 어느 그룹에 있는지 확인 가능
- Small group에 k번째로 작은 숫자가 포함된 경우
- k번째 작은 숫자를 Small group에서 찾기
- Large group에 k번째로 작은 숫자가 포함된 경우
- (k-|Small group|-1)번째로 작은 숫자를 Large group에서 찾기
2. 선택 문제 알고리즘
Selecttion(A, left, right, k):
피봇을 A[left]~A[right]에서 랜덤하게 선택하고, 피봇과 A[left]의 자리를 바꾼 후, 피봇과
배열의 각 원소를 비교하여 피봇보다 작은 숫자는 A[left]~A[p-1]로 옮기고, 피봇보다 큰 숫자
는 A[p+1]~ A[right]로 옮기며, 피봇은 A[p]에 놓는다.
S = (p-1)-left+1
if(k<=S) Selection(A,left, p-1, k)
else if(k = S+1) return A[p]
else Selection(A,p+1,right, k-S-1)3. 알고리즘 수행 과정
-
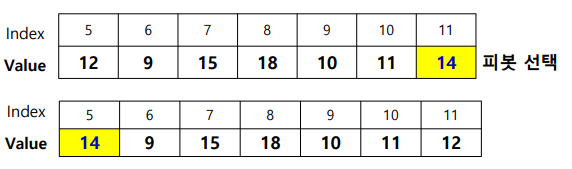
주어진 리스트 A에서 7번째로 작은 수를 찾는 문제

-
Selection(A,0,11,7) 호출

-
피봇 이동(편하게 분할하기 위함)

-
각 원소들의 크기를 비교후 위치 이동

-
피봇을 제자리로 이동(j위치)

-
Small group의 크기를 계산
S = (p-1)-left+1 = (4-1)-0+1 = 4- 7번째이니 Large group에서 찾기(2번째로 큰 수)
-
Selection(A,5,11,2) 호출
-
자리바꿈
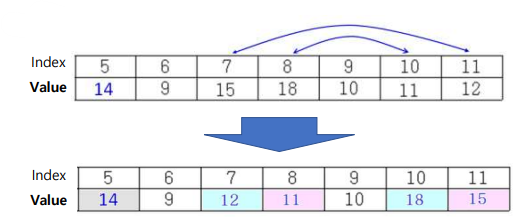
-
피봇을 제자리로 이동

-
Small group 크기 계산
S = (p-1)-left+1 = (9-1)-5+1 = 4- Large group에서 2번째로 큰 수를 찾고 있었으니 Small group에서 찾기
-
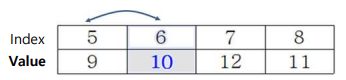
Selection(A,5,8,2) 호출

-
원소간 이동없이 피봇 원위치
-
Small group의 크기 계산
S = (p-1)-left+1 = (6-1)-5+1 = 1 -
if(k<=S)는 false -
else if(k=S+1)는 true- A[6] = 10을 return
4. 선택 알고리즘 고려사항
- 선택 알고리즘은 분할정복이며, 동시에 랜덤 알고리즘임
- 피봇을 랜덤하게 정하기 때문
- 이 또한 피봇이 한쪽으로 치우치면 알고리즘의 효율성이 저하됨
- 선택 알고리즘이 호출될 때 마다 한쪽으로 치우칠 확률
- 동전을 던질 때 한쪽면이 나오는 확률과 동일: 1/2
5. 분할에 대해
- Good/Bad 분할 정의

- 좋은 피봇을 선택할 확률과 나쁜 피봇을 선택할 확률은 같음
- 즉, 1/2확률로 good 피폿을 선택
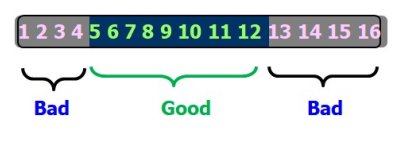
- 즉, 1/2확률로 good 피폿을 선택
6. 시간복잡도
- good 분할을 수행할 확률: 1/2
- 2회 호출마다 good분할이 이루어지니 good분할만 연속적으로 이루어졋을 때의 시간복잡도를 구현한 후 그 값에 2를 곱하여 평균경우의 시간 복잡도를 계산 가능
- 연속된 Good 분할

- 입력의 크기가 n에서 3/4배로 연속적으로 감소되며, 입력 크기가 1인 경우에는 더 이상 분할 불가
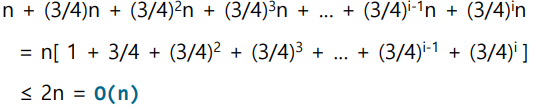
- 평균 2회에 good 분할이 이루어지니 2*O(n) = O(n)
- 입력의 크기가 n에서 3/4배로 연속적으로 감소되며, 입력 크기가 1인 경우에는 더 이상 분할 불가
7. 선택 알고리즘과 이진 탐색
- 유사성
- 이진 탐색에서는 범위를 1/2씩 좁혀 나가며 찾고자 하는 숫자를 탐색
- 선택 알고리즘은 피봇으로 분할하여 탐색 범위를 좁혀 나감
- 공통점
- 부분 문제들을 별도로 취합하는 과정이 불필요
