Merge Sort(합병정렬)

• 입력이 2개의 부분 문제로 분할되고, 부분 문제의 크기가 1/2로 감소하는 분할정복 알고리즘
• 알고리즘 실행 과정
  • n개의 데이터들은 n/2개씩 2개의 부분문제로 분할
  • 더 작은 부분 문제들로 불할할 수 없을 때 까지 주어진 데이터들을 계속해서 분할
  • 두 데이터를 합병정렬하여 정렬(정복)
  • 2개의 정렬된 부분을 합병하여 정렬(정복)
• 합병 과정이 문제를 정복하는 것

1. 합병 과정

• 두 개의 정렬된 리스트를 하나의 정렬된 리스트로 합치는 과정

배열 A: 6 14 18 20 29
배열 B: 1 2 15 25 30 45
배열 C: 1 2 6 14 15 18 20 25 29 30 45

2. 합병 정렬 알고리즘의 의사코드

• 전체 코드

Algorithm MergeSort(A, left, right)
  if(left<right)
  {
    mid = floor((left+right)/2)
    MergeSort(A, left, mid)
    MergeSort(A, mid+1, right)
    Merge(A, left, mid, right)
  ]

• 정복 과정

Algorithm Merge(A, left, mid, right)
  b1 = left; e1 = mid; b2 = mid+1; e2 = right;
  Initialize a temporary array sortedp[];
  index = 0;
  
  while(b1 <= e1 and b2<=e2)
    if(A[b1] <A[b2]) sorted[index] = A[b1]; b1++; index++;
    else sorted[index] = A[b2]; b2++; index++;
  Copy all remaining elements in the sub-lists to sorted[];
  Copy all elements in sorted[] to A[];

3. 합병 정렬 과정

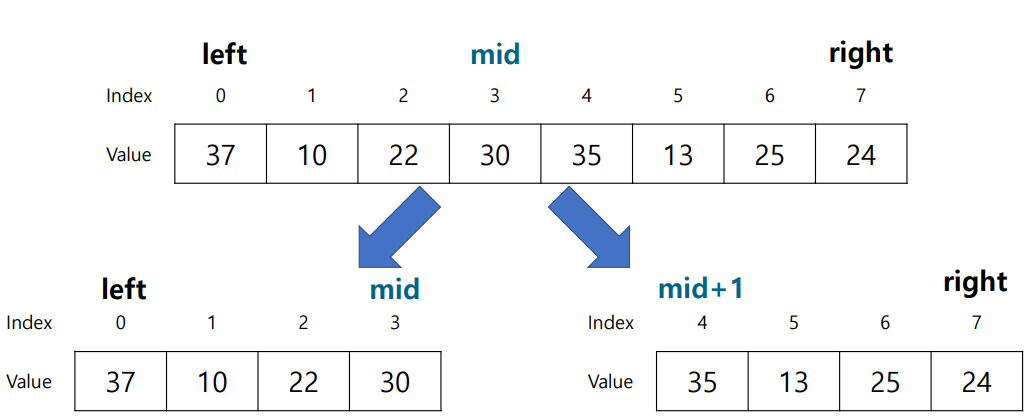
• 분할 과정

  • Array.size()/2번째 원소를 mid로 지정
  • left~mid & (mid+1)~right로 배열을 나눔
    

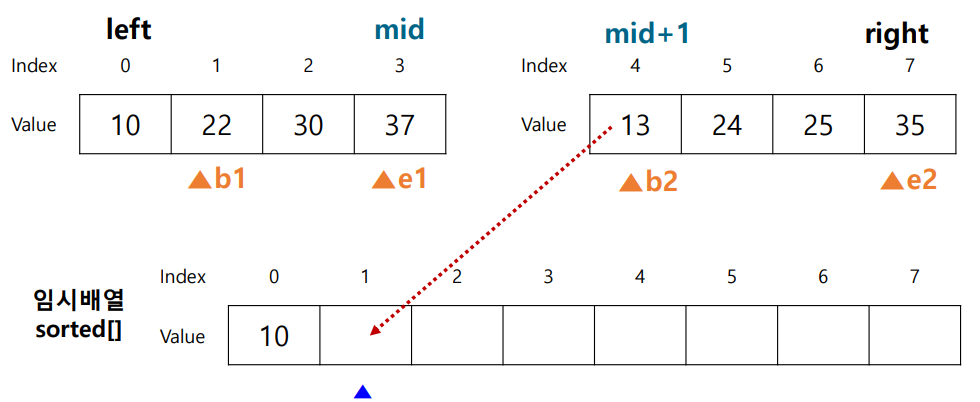
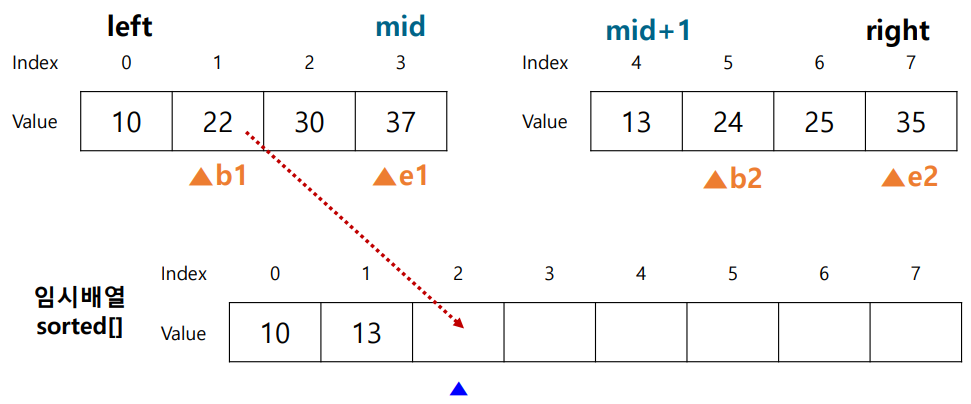
• 합병 과정

  • b1번째 원소와 b2번째 원소를 비교하여 더 작은 원소를 임시배열에 넣음
  • 더 작은 원소의 포인터를 1증가시켜 다음 원소를 가리킴
  • 반복
  • 한 배열의 b==e가 된다면 반복을 중지
  • 남은 배열의 원소를 임시배열에 차례대로 넣음
    
    
    
    

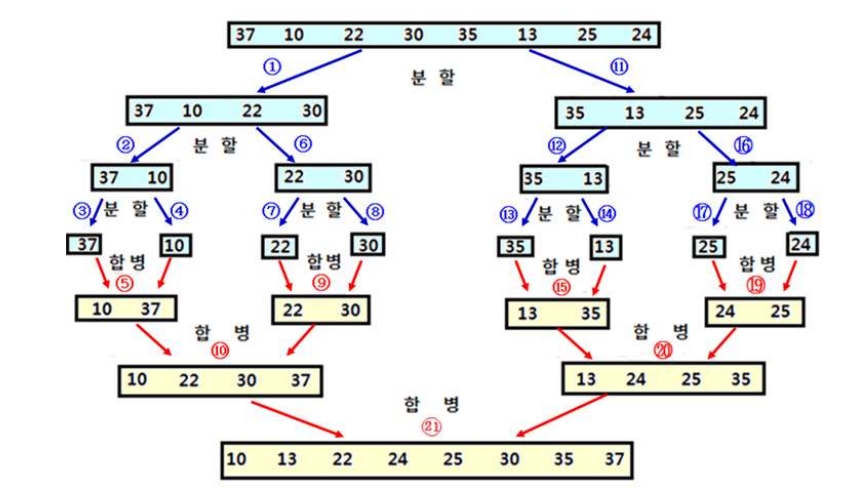
• 최종 이미지
  

4. 합병 정렬 시간복잡도

• 분할 과정은 배열의 중간 인덕스 계산과 2회의 순환호출이므로 O(1)시간 소요
• 합병 과정의 수행시간은 입력의 크기에 비례
  • 2개의 정렬된 배열 A와 B의 크기가 각각 m, n이라면, 최대 비교 횟수는 m+n-1
  • 합병의 시간복잡도: O(m+n)
• 합병 정렬에서 수행되는 총 비교 횟수(각 합병에 대한 비교횟수를 모두 더한 것)
  • 합병은 입력 크기에 비례하므로 각 층에서 수행된 비교 횟수는 O(n)
• 층 수 계산: log scale로 증가함
  • log2n
• 최종 계산
  • 층수 O(n) = log2nO(n) = O(nlogn)

5. 합병정렬의 단점

• 대부분의 정렬 알고리즘들은 입력을 위한 메모리공간과 O(1)크기의 메모리 공간만을 사용하여 정렬 수행
• 합병정렬은 임시배열을 사용하기 때문에 공간복잡도는 O(n)
  • 2개의 정렬된 부분을 하나로 합병하기 위해, 합병된 겨로가를 저장할 곳이 필요하기 때문