퀵 정렬(Quick Sort)
- 부분 문제의 크기가 일정하지 않은 형태의 분할 정복 알고리즘
1. 퀵 정렬의 아이디어
- 퀵 정렬은 피봇(pivot)이라 일컫는 배열의 원소를 기준으로 함
- 피봇보다 작은 숫자들은 왼쪽, 큰 숫자는 오른쪽으로 분할
- 분할 시, 피봇은 분할된 배열에 포함되지 않고 위치가 고정됨
- 위의 과정을 순환
2. 퀵 정렬 알고리즘의 의사코드
- 전체 의사코드
Algorithm QuickSort(A, left, right):
if(left<right)
p = partition(A, left, right);
QuickSort(A, left, p-1);
QuickSort(A, p+1, right);- 부분 리스트 정렬과 피봇 인덱스를 반환하는 의사코드
Algorithm partition(A, left, right):
swap(A[left], A[p])
pivot = A[left]
i = left+1
j = right;
while(i<j)
while(i<right && A[i]<pivot) i++
while(j>left+1 && A[j]>pivot) j--
if(i<j) swap(A[i], A[j])
swap(A[left], A[j])3. 퀵 정렬 수행 예시
-
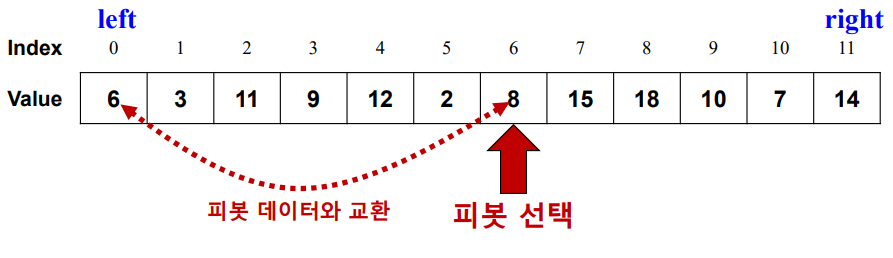
P(pivot index)를 결정하기 위해 partition(A,left right)호출

-
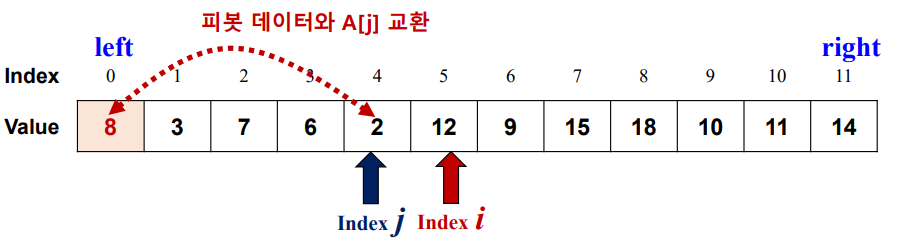
분할하기 쉽도록 피봇 데이터를 왼쪽으로 이동
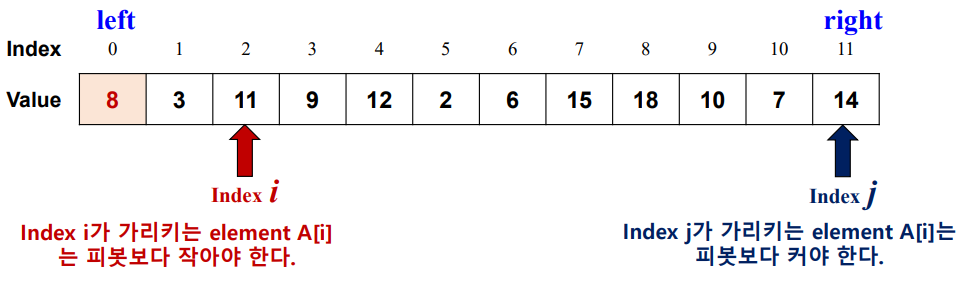
-
왼쪽(i)과 오른쪽(j) two pointer를 사용하여 원소 비교
- 작은 것을 왼쪽으로 큰 것을 오른쪽으로
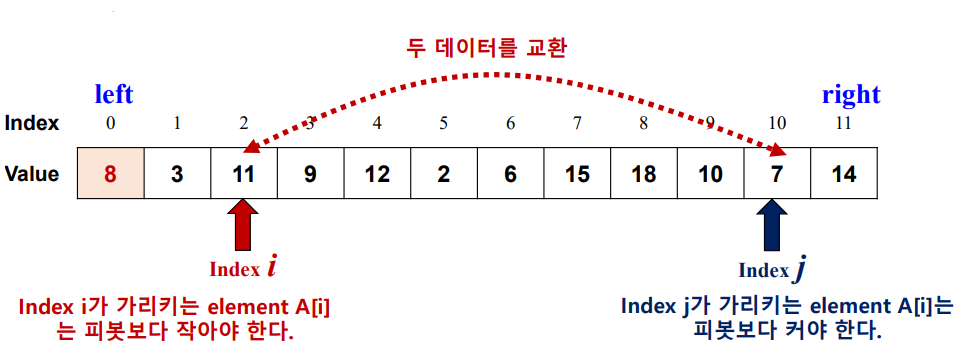
- 작은 것을 왼쪽으로 큰 것을 오른쪽으로
-
i가 j보다 커지면 탐색종료
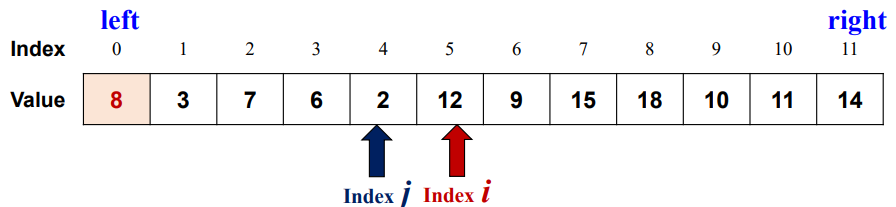
-
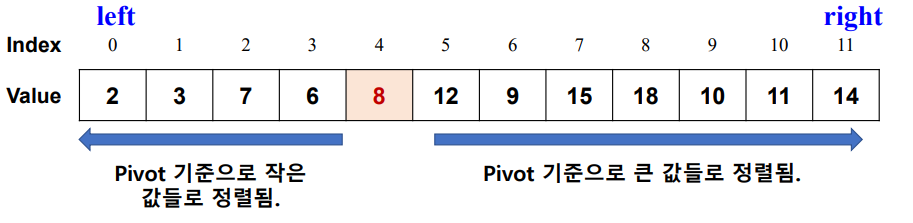
pivot를 원래 위치로 설정
- i와 j가 만난 구간이 중간 수 즉, pivot이 위치할 자리
- i와 j중 j가 작은 수를 가리키고 있고, pivot의 현재 위치가 작은 수 위치(왼쪽)에 있으니 j와 변경
-
최종 결과
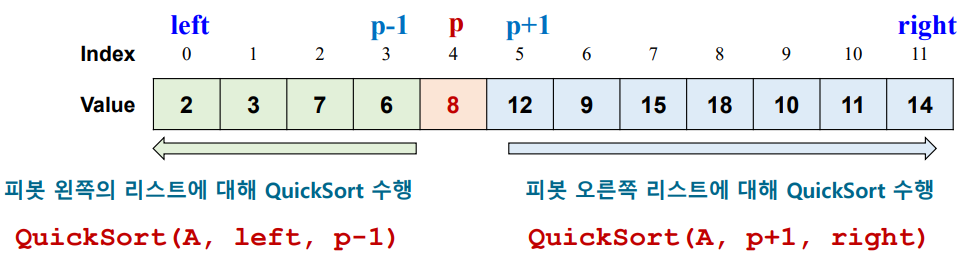
-
반복
4. 시간복잡도
- 퀵 정렬은 피봇 선택에 의해 성능이 좌우됨
- 피봇이 한쪽으로 치우쳐져 있다면, 낮은 성능의 정렬법
- 최악의 시간복잡도: O(n^2)
- 최선의 경우: 동등한 길이로 분할되는 경우
- 비교횟수: O(n)
- 총 비교 횟수: O(n) x 층수 = O(n)*logn
- 최선의 시간복잡도: O(nlogn)
- 평균의 경우 시간복잡도
- pivot을 항상 랜덤하게 선택한다면, O(nlogn)
5. 피봇 선정 방법
- 랜덤 선정 방법
- Median of Three: 왼쪽, 중간, 오른쪽 원소의 중간값을 피봇으로 사용

- Median-of-Medians (Tukey’s Ninther): 3등분 후 Median of Three방법을 실행한 뒤 다시 Median of Three를 실행
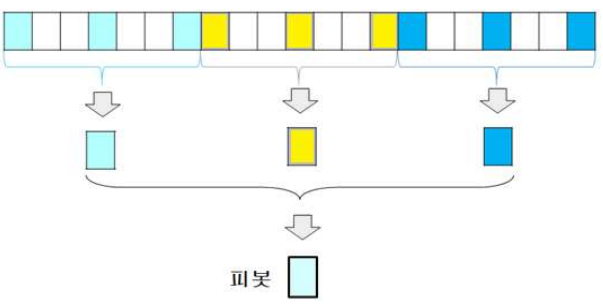
6. 성능 향상 방법
- 입력의 크기가 매우 클 때, 퀵 정렬의 성능을 더 향상시키기 위해서, 삽입정렬을 동시에 사용
- 입력의 크기가 작을 땐 퀵정렬이 삽입정렬보다 빠르지 않음
- 퀵은 순환 호출로 수행되기 때문
- 입력의 크기가 작을 땐 퀵정렬이 삽입정렬보다 빠르지 않음
- 결론적으로 부분 문제의 크기가 일정수준 이하로 작아진다면, 분할(순환 호출)을 중단하고 삽입정렬을 사용하자
