집합 커버 문제

• 문제 설명
  • n개의 원소를 가진 집합 U
  • U의 부분집합들을 원소로 하는 집합 F가 주어짐
  • F의 원소들로 구성된 집합 중에서 어떤 집합들을 선택하여 합집합 연산을 수행하면 집합 U와 같게 되는가?
• 집합 F에서 선택하는 집합들의 수를 최소화하는 문제

예제문제-신도시 학교 배치

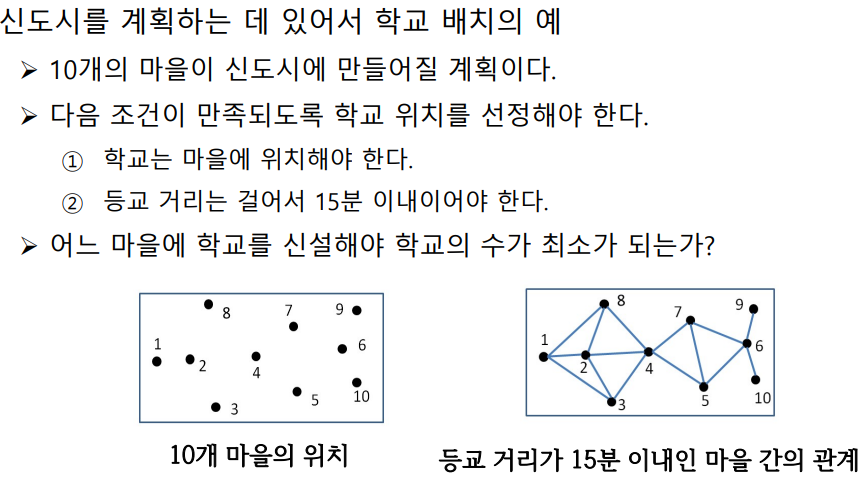
1. 정답

• 2번 마을에 학교를 만들면
  • 1,2,3,4,8 마을의 학생들이 15분 이내에 등교 가능
  • 즉, 마을 1,2,3,4,8 이 커버
• 6번 마을에 학교를 만들면
  • 5,6,7,9,10 이 커버
• 2와 6에 학교를 배치하면 모든 마을 커버 가능
  • 최소의 학교수 = 2

2. 단순한 풀이법

• F에 있는 집합 S1,..., Sn의 모든 조합을 1개씩 합집합하여 U가 되는지 확인
• U가 되는 조합의 집합 수가 최소인 것을 찾음
• 시간복잡도: O((2^n)-1)
  • 실용성 없음;;

3. 집합커버 알고리즘

• 위와 같은 문제를 해결하기 위해 최적해를 찾는 대신 최적해에 근접한 근사해(Approximation solution)을 찾음
• 수행과정
  • U의 원소를 가장 많이 커버하는 집합 선택
  • U = U/(원소를 가장 많이 커버하는 집합) (/는 차집합 기호)
  • (원소를 가장 많이 커버하는 집합)을 F에서 제거
  • (원소를 가장 많이 커버하는 집합)을 C에 추가
  • 처음과정 반복
• 집합 커버 알고리즘을 사용하면 3개의 학교를 사용하는 근사해를 구함
  

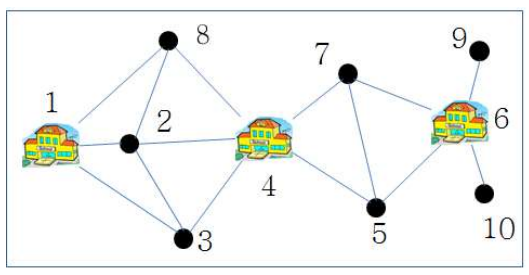
4. 집합커버 알고리즘 시간복잡도

• While 실행 횟수: 최대 n회
  • 루프가 1회 수행될 때마다 집합 U의 원소 1개씩만 커버된다면, 최악의 경우 루프가 n번 수행되어야 하기 때문
• 루프가 1회 수행 시
  • S_i를 U와 비교해야 함
  • S_i들의 수가 최대 n이라면, 각 S_i와 U의 비교는 O(n) 시간이 걸리므로, O(n^2)
  • 집합 U에서 집합 S_i의 원소를 제거하므로 O(n) 시간이 소요
  • S_i를 F에서 제거후, Si를 C에 추가하는 과정 O(1)
• 시간복잡도: n * O(n^2) = O(n^3)