최단경로 문제

• 최단 경로 문제
  • 주어진 가중치 그래프에서 어느 한 출발점에서 또 다른 도착점까지의 최단경로를 찾는 문제
• 최단 경로를 구하는 알고리즘 종류
  • 단일 정점으로부터 나머지 모든 정점가지의 최단거리를 계산하는 알고리즘
  • 모든 정점간 최단 거리를 계산하는 알고리즘

다익스트라 알고리즘

• 음의 가중치가 없는 그래프에서, 시작 정점인 s에서 모든 정점까지의 최단 거리를 계산
• 출발점으로부터 최단 거리가 확정되지 않은 정점들 중에서 출발점으로부터 가장 가까운 정점을 추가하고, 그 정점의 최단 거리를 확정하는 방법으로 진행
• 이 때, 두 정점간의 최단 거리를 계산하는 원리는 다음과 같음

if(D[v_min]+간선(v_min,w)의 가중치<D[w])		//기존 가중치 보다 작다면
  D[w] = D[v_min]+간선(v_min, w)의 가중치	// 업데이트

1. 다익스트라 알고리즘의 수행과정

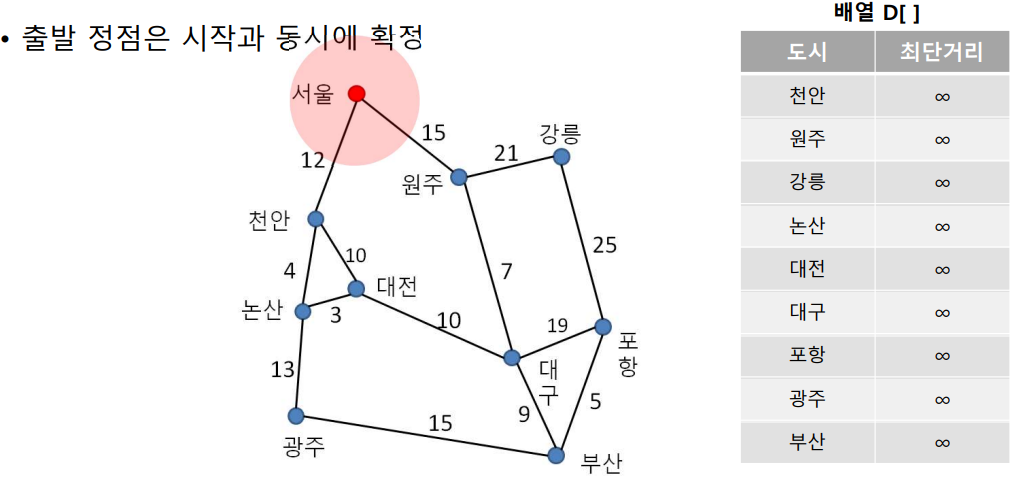
• 출발 정점 설정
  
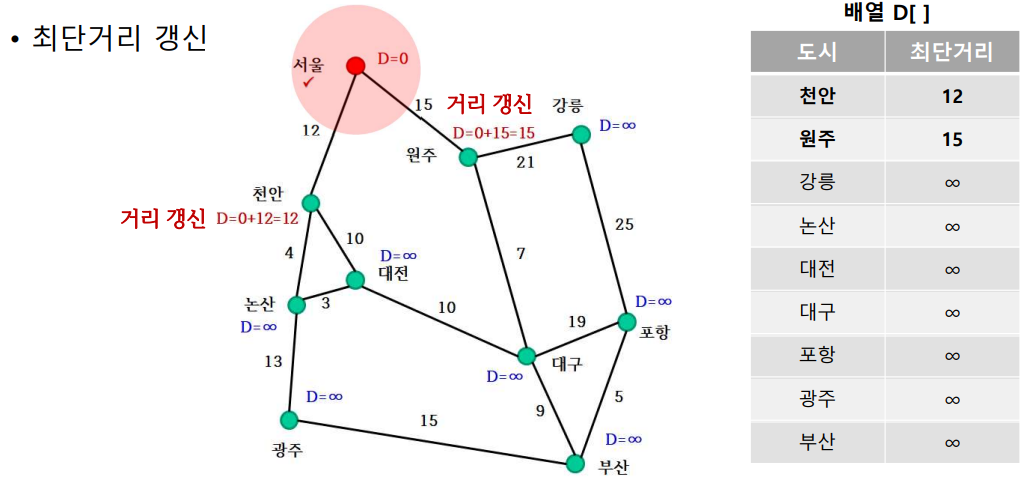
• 최단거리 갱신
  
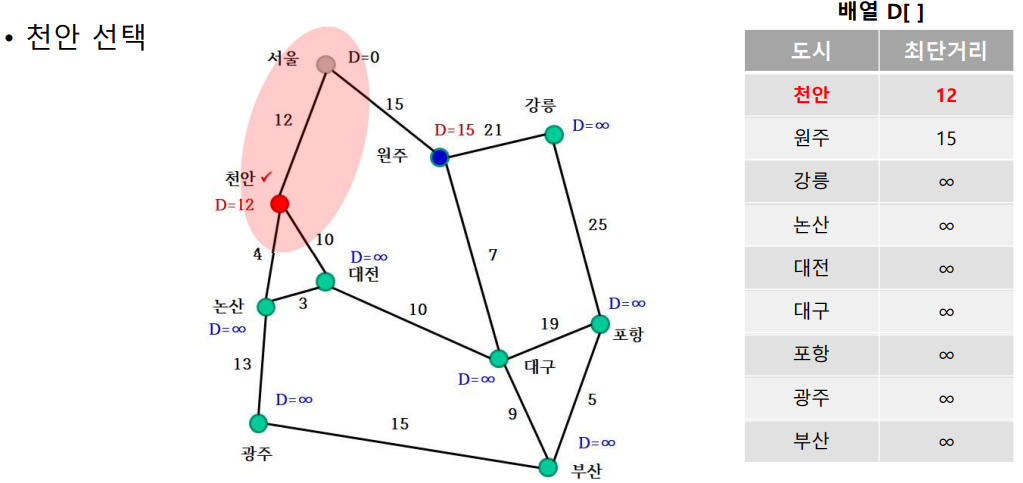
• 천안 선택
  
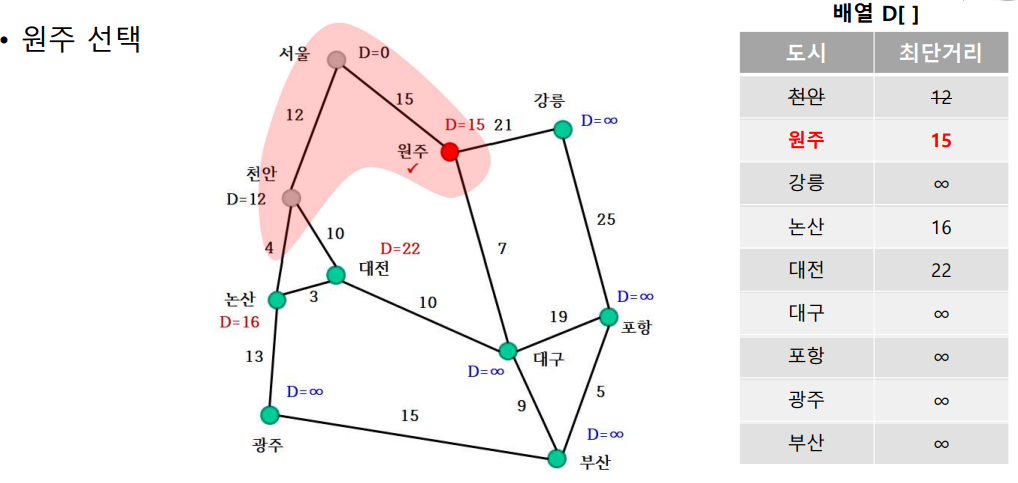
• 원주 선택
  

...

• 최종
  

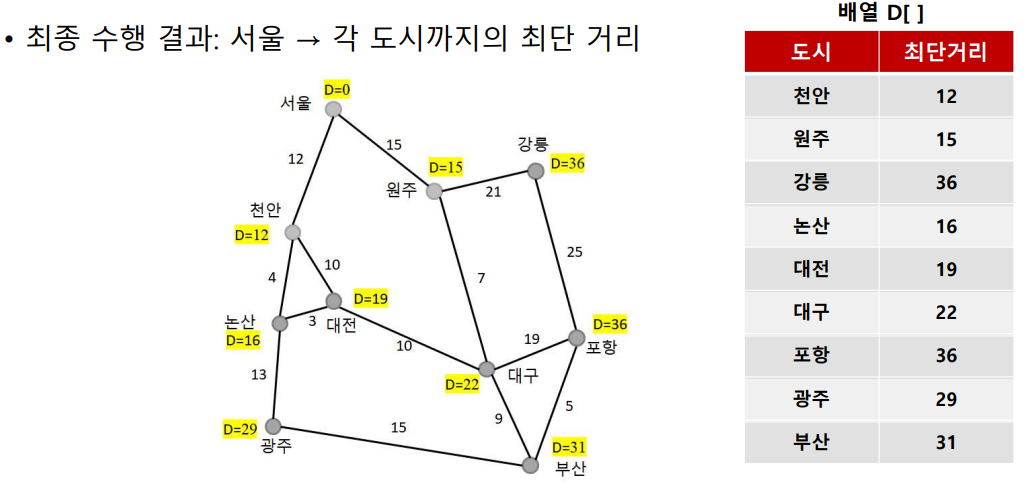
2. 다익스트라 알고리즘의 시간복잡도

• While 반복문이 (n-1)회 반복되고, 1화 반복될 때
  • 최소 거리를 가진 점을 찾기 위해 O(n) 시간이 소요
    - 배열 D에서 최솟값을 찾기 때문
  • 거리를 갱신시키는데 소요되는 시간은 최소 거리를 가진 점과 연결된 노드의 수와 같으니 O(n)
• 최단 거리의 시간복잡도
  • (n-1) * {O(n)+O(n)} = O(n^2)
  • Prim 알고리즘과 같이 최소 힙을 사용하면 O(mlogn)
  • 따라서 간선의 수가 O(n)이면 총 시간복잡도는 O(nlogn)

---

소스코드

#include <iostream>
#include <vector>
#include <queue>
#define INF 200000001
#define MAX 100005
using namespace std;
typedef pair<int, int> pii;

vector<pii> nodes[MAX];
int dist[MAX];

void dijkstra(int s)
{
	priority_queue<pii> pq;

	dist[s] = 0;
	pq.push({ 0,s });

	while (!pq.empty())
	{
		int cost = -1*pq.top().first;
		int cur = pq.top().second;
		pq.pop();

		//이미 최단 거리 정보가 있다면 pass
		if (dist[cur] < cost) continue;

		for (pii curNode : nodes[cur])
		{
			int viaCost = cost + curNode.first;

			if (viaCost < dist[curNode.second])
			{
				dist[curNode.second] = viaCost; //거리갱신
				pq.push({ -1*viaCost,curNode.second }); //탐색
			}
		}
	}
}

int main()
{
	ios::sync_with_stdio(false); cin.tie(NULL);

	int N, M, S, E; cin >> N >> M >> S >> E;
	for (int i = 0; i < MAX; i++) dist[i] = INF;
	for (int i = 0; i < MAX; i++) nodes[i].clear();
	for (int i = 0; i < M; i++)
	{
		int a, b, d; cin >> a >> b >> d;
		nodes[a].push_back(make_pair(b, d));
		nodes[b].push_back(make_pair(d, a));
	}

	dijkstra(S);
	cout << dist[E];
	return 0;
}