Abstract

• 망의 깊이가 길수록 학습이 어렵지만, 본 논문에서는 residual learning framework을 이용하여서 기존의 심층망들의 학습을 완화하는 방법을 제시한다
• 심층망일수록 overfitting, gradient의 소멸, 연산량의 증가 등의 필연적인 문제들이 발생한다. (gradient의 vanish보다는 explode가 처리하기 쉬움)
• 더 깊은 망에 대해서도, 정확도 향상과 상대적으로 쉬운 최적화를 달성할 수 있었다고 한다. (VGGNet의 8배인 152layer를 자랑한다.)
• 앙상블 기법을 적용하여서 오차를 3.75%까지 줄였음

Introduction

• 심층 신경망은 추상화에 대한 low/mid/high level feature들을 classifier과 함께 multi-layer 방식으로 통합한다. 여기서 추상화 level은 layer 수에 비례한다
• depth가 성능과 비례한다는 점에서, layer를 쌓는만큼 더 쉽게 네트워크를 학습하는 것이 가능한지?에 대한 의문을 가지기 시작했다
• vanishing/exploding gradients는 convergence의 큰 방해요소였고, SGD를 적용한 10개의 layer까지는 normalization이나 batch normalization등과 같은 intermediate normalization layer를 사용했을 경우 문제가 크게 없었다고 한다
• 심층 신경망이 깊어지면서 성능이 최고점 부근에 달할때 degradation 문제가 발생하기 시작하였고, 이는 깊어진 신경망에 의한 train error증가 → test error 증가로 인한 정확도 포화 및 감소를 뜻한다.
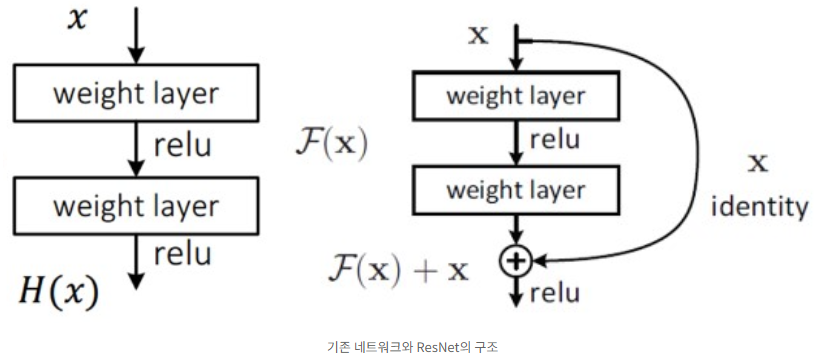
• 기존 네트워크 : input x → layers → output H(x)
  ResNet : input x → layers → output F(x) = H(x) - x
  x는 바꿀 수 없는 입력값이기에 F(x) = 0일 때가 최적의 해이다.
  즉, H(x) = x로 mapping하는 것이 학습의 목표이다.
• 기존엔 알 수 없는 H(x)를 학습시켜야 한다는 점이 어려웠지만, ResNet은 H(x) = x라는 최적의 목표값이 pre-condition으로 제공되기에 identity mapping이 쉬워진다.
• 기존과 같은 구조와 같은 파라미터 수를 가진 채로 입력을 출력으로 연결해주는 합연산 shortcut만 추가해주면 되기에 덧셈을 제외하고는 연산량의 증가나 영향은 딱히 없다는 장점이 있다.
• 곱셈 연산 → 덧셈 연산으로 변형되면서 몇 개의 layer를 건너뛰는 효과로 두 가지의 효과가 있었다고 한다 :
  • forward/backward path가 단순해짐
  • vanishing gradient를 해결함

Related Works

• original vector보다 residual vector를 encoding하는 것이 vector quantization에 있어서 훨씬 효과적이다.
  (vector quantization : 특정 vector X를 Class vector Y로 mapping하는 것)
• low-level 문제에서 기존의 멀티 그리드 방식을 이용하여 더 작은 하위 문제들로 나누어서 봐왔는데, 이러한 하위 문제들이 작은 scale과 큰 scale 사이에서 residual을 담당하게 된다. 대신 두 scale간의 residual vector를 가리키는 변수에 의존하는 방식으로 pre-conditioning을 해준다. 이렇게 문제를 합리적으로 재구성하고 전제 조건을 다루는 것은 문제의 최적화를 간소화해준다.
• shortcut connection으로 인해서

0으로 수렴되지 않음 → 절대 닫힐 일이 없음 → 항상 모든 정보가 통과 → 지속적인 residual training이 가능함

Method

• 실제로는 identity mapping이 최적일 가능성이 매우 낮지만, residual network를 사용한 pre-conditioning으로 인해 optimal function이 zero mapping보다 identity mapping에 가깝다면, solver이 identity mapping을 참조하여 작은 변화를 학습하는 것이 새로운 미지의 function을 학습하는 것보다는 쉬운 일이라고 주장하고 있다.

• shortcut connection은 파라미터나 연산 복잡성을 추가하지 않는다. F + x 연산 시에 서로의 차원이 맞지 않으면 linear projection인 Ws을 곱해주어서 차원을 맞춰줄 수 있다.

• Plain Network는 VGGnet을 baseline으로 이용하여서 설계되었다고 한다.
  conv filter의 size가 3x3이고 다음 2 가지 규칙을 따른다 :

  • output feature map의 size가 같은 layer들은 모두 같은 수의 conv filter를 사용한다.
  • output feature map의 size가 반으로 줄면 time complexity를 유지하기 위해서 conv filter의 수를 2배로 늘려준다.

• 추가적으로, downsampling 수행 시에 pooling하지 않고 stride가 2인 conv filter를 사용하고, 모델 끝단에 GAP을 사용하고, size가 1000인 FC layer와 Softmax를 사용한다. (stride는 보통 shortcut의 뛰어넘는 size와 동일하게 설정)

• ResNet은 Plain model을 기반으로 shortcut connection을 추가하여 구성된다. 차원이 같을 떄는 identity shortcut을 바로 적용하면 되지만, 차원이 증가했을 경우에는 2가지 선택권이 있다 :

  • zero padding을 적용하여서 차원을 키운다.
  • 앞서 다뤘던 projection shortcut을 사용한다. (1x1 convolutuion)