[Lecture 1] The Geometry of Linear Equations

첫 시간에는 방정식을 바라보는 관점과, 이를 시각적으로 어떻게 표현할 수 있는지를 주로 다루었다.

방정식을 바라보는 시각은 크게 2가지로, Row picture와 Column picture로 나눌 수 있다.
예시로 아래 방정식을 두 가지 관점에서 바라보겠다.

예시의 방정식은 아래와 같은 Matrix form으로 표현 가능하다.

1. Row picture : 방정식을 행으로 바라보는 것.

위 예시 방정식을 그대로 좌표계로 표현하면 아래 그림과 같다.

여기서 각 방정식의 가능한 해는 $R^2$ 공간에서 직선을 이룬다. 두 방정식을 동시에 만족하는 해는 두 직선이 서로 공유하는 공간이 될 것이고, 해당 예시에서는 점이 그 공간이 된다. 따라서 두 직선이 교차하는 지점이 해당 예시의 해가 될 것이다.
마찬가지로 3 by 3 matrix가 예시로 주어졌을 경우, 각 row의 가능한 해는 $R^3$ 공간에서 평면을 이룰 것이다. 여기서 세 평면이 만나는 점이 해가 될 것이다.

2. Column picture : 방정식을 열로 바라보는 것.

위 예시 방정식을 vector 형태로 표현한다면 아래와 같이 볼 수 있을 것이다.

이는 $\begin{bmatrix} 2 \\ -1 \end{bmatrix}$와 $\begin{bmatrix} -1 \\ 2 \end{bmatrix}$의 선형결합으로 $\begin{bmatrix} 0 \\ 3 \end{bmatrix}$을 만들어야 한다고 볼 수 있다.
마찬가지로, $x=1, y=2$를 각각 대입한다면 위 선형 결합을 만족하는 것을 알 수 있다.

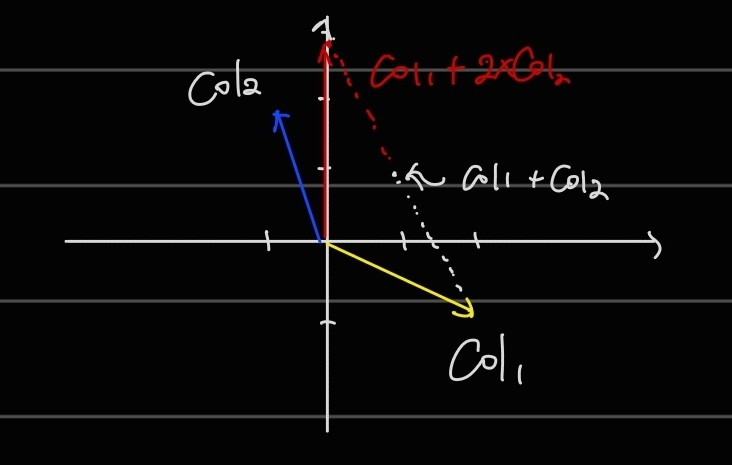
여기에서, $\begin{bmatrix} 2 \\ -1 \end{bmatrix}$와 $\begin{bmatrix} -1 \\ 2 \end{bmatrix}$의 모든 가능한 선형 결합을 취한다면 위 좌표계의 모든 평면을 채울 것이다.
여기에서 우리는 $Ax = b$에서 $Ax$가 가중치 $x$를 고려한, A의 column들 간의 선형 결합임을 알 수 있다.

위 예시 방정식의 해는 $\begin{bmatrix} 1 \\ 2 \end{bmatrix}$이고, Row picture든 Column picture든 무관하게 같은 결과를 내는 것을 알 수 있다.

다만 추후 선형대수에서 다룰 내용들을 감안한다면 Column picture로 위 식을 바라보는 것이 유리할 것이다.

결국 우리가 당면할 문제 중 하나는 $Ax = b$에 대해, 모든 $b$에 대해 방정식을 풀 수 있는지가 될 것이다. 이는 행렬 $A$의 Column들의 선형 결합으로 모든 n차원 공간을 채울 수 있는지와 같은 의미이다.

만일 모든 $b$에 대해 문제를 풀 수 없는 경우는 모든 column이 같은 방향, 같은 공간에 놓여 있을 경우가 될 것이다.
따라서 $b$가 해당 column이 차지하고 있는 특정한 공간 상에 있을 경우에만 문제를 풀 수 있을 것이다.