[DB] #02. Relational Data Model
Database

2.1 Relational Data Model
Overview
-
E.F. Codd(1970) 최초 제안
-
매우 Simple → 데이터 표현하고 다루는 데 Strong
-
개념적 간단함 : 집합이론, 일차 수학논리 사용
-
데이터베이스 = 관계(relation) + 무결성 제약(integrity constraint)의 묶음(collection)
-
테이블 형식
- student 라는 개체를 tuples(행) & attibutes(열)로 관리
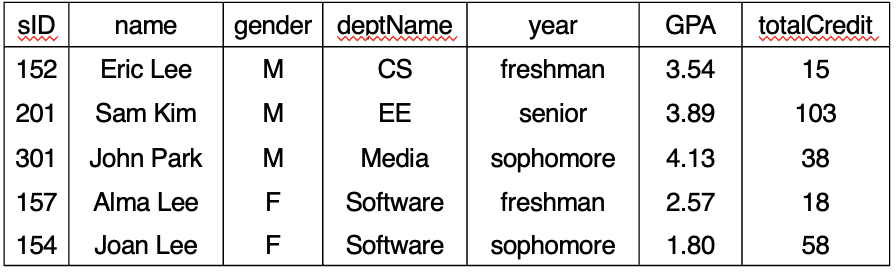
- 7개의 attribute, 5개의 tuple
- 각 속성은 attribute head를 가짐 : sID, name, gender, …
- student 라는 개체를 tuples(행) & attibutes(열)로 관리
-
Equivalent Terms
- relation - table
- tuple - record, row
- attribute - column
Attibutes
- domain을 가진다.
- 속성값으로 허용할 수 있는 값의 집합
- ex. year : {null, 1, 2, 3, 4}
- 속성에 대한 데이터 타입 정의로부터 도메인 유추 가능
- atomic 해야한다
- 더이상 나누어질 수 없어야 함 → ex. 정수, 실수, 문자열, 시간, 날짜, 타임스태프 등
- cf) non-atomic
- ex. multi-value, set, bag(중복 허용), list, composite values 등
- 군집 데이터를 정의
- 서로 상이한 대상 표시
- 더이상 나누어질 수 없어야 함 → ex. 정수, 실수, 문자열, 시간, 날짜, 타임스태프 등
- null value를 가진다.
- null값이 default
Relation Schema & Instance
- Relation Schema
- 관계명(속성명)의 나열 + 속성의 데이터 타입 + 무결성 제약
- attributes : A1, A2, … , An → schema : R = (A1, A2, …, An)
- Instance
- 각 속성 도메인값의 모든 조합에서 부분집합
- domain의 카티시안곱의 부분집합
- domains : D1, D2, …, Dn → Instance : D1 x D2 x .. x Dn 의 부분집합 → 관계형 데이터 모델
- individual values를 가질 수 있다. → 특정 시점 Table 값들의 집합 : Instance
- instance : n-tuples
Relational Databases
- 관계의 집합 + 제약 조건의 집합
- Integrity constraints
- Key constraint. : primary key는 중복 X
- Entity constraint : primary key는 NULL값 X
- Referential integrity constraint (참조 무결성 제약) 등
- 순서는 중요 X
-
relation 간 순서 X
-
tuple 간 순서 X
→ 관계형 데이터 모델의 중요한 특징
-
데이터베이스 처리 편리함
-
관계 접근 시 특별한 제한 X (cf. 계층/네트워크 모델 : 테이블간 상하관계 존재)
-
Sample University Database
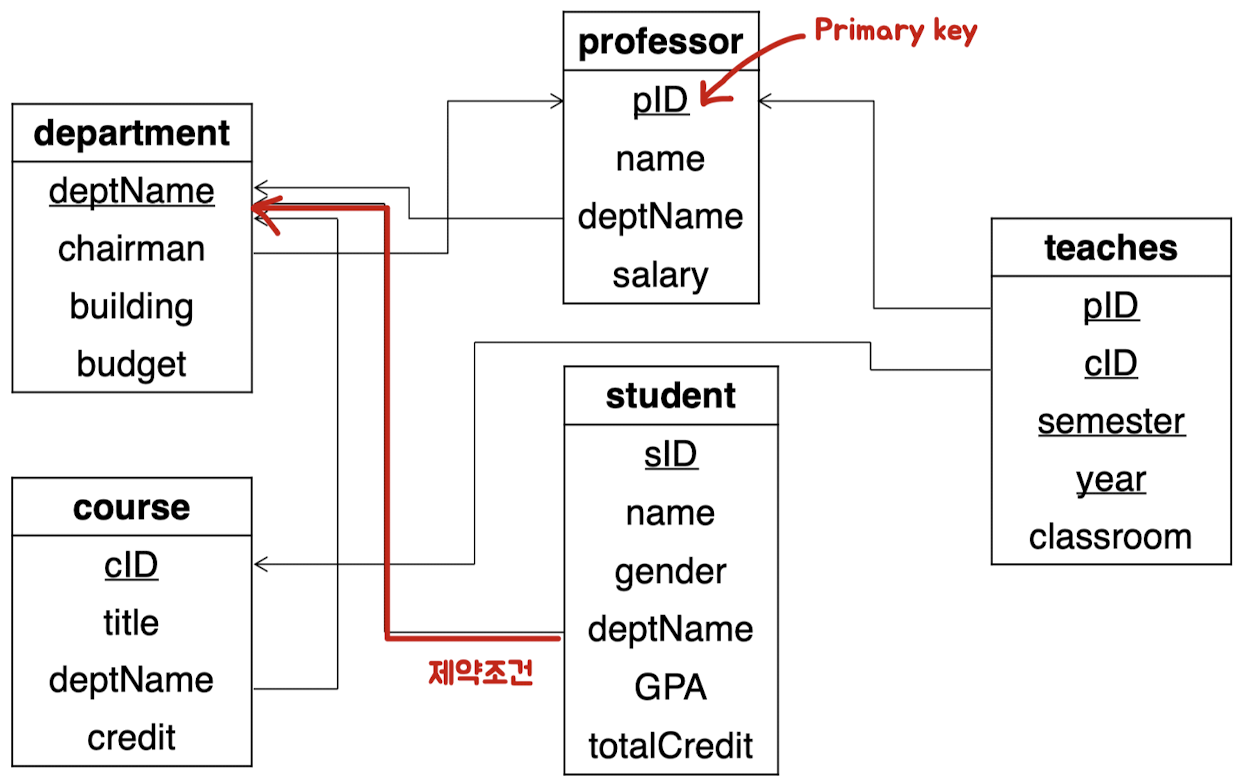
- 5개의 Relation
- 속성 밑줄 : Primary key
- teaches 관계의 primary key : 4개의 속성 연결(concatenation)
- pID, cID, semester, year
- 속성 하나하나는 primary key (X)
- 화살표 : 참조 무결성 제약 표시 ex. teaches의 cID = course의 cID 속성을 참조하는 foreign key (외래키)
Keys
- K는 R(속성)의 부분집합 (같거나 포함된다)
- Super Key
- 가장 큰 개념
- identify 각 행을 유일하게 식별할 수 있는 하나 또는 그 이상의 속성 집합
- 유일성 만족하면 super key !
- Candidate Key (후보키)
- 각 행을 유일하게 식별할 수 있는 최소한의 속성 집합
- minimal한 Super Key (minimum함 X)
- 단일속성, 2개의 속성을 가진 두 개의 후보키 존재할 수도 있음 ! ⁉️
- Primary Key (기본키, 주키)
- 후보키들 중 설계자가 하나를 선택한 키 → 최소성, 유일성 만족
- Null 값 X, 중복된 값 X
- 테이블에서 기본키는 오직 1개만 지정
2023.09.14
Referential Integrity Constraint
-
참조 무결성 제약
-
관계형 데이터 모델에만 존재하는 제약
→ 데이터 간의 관계를 ‘값’(포인터X)으로 표현하기 때문
-
특정 속성에 나타나는 모든 값은 반드시 다른 속성에도 나타나야 한다.
→ 특정 속성에 나타나는 모든 값은 다른 속성 값의 일부분이어야 한다.
-
다른 테이블 참조 : Foreign Key
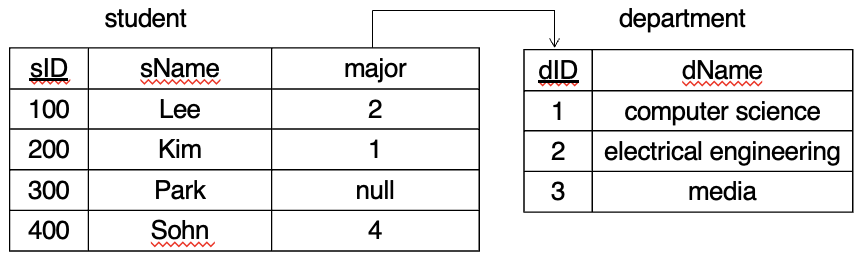
- {null, 1, 2, 3} 집합 외의 값 불가능
- major : department(dID)를 참조하는 외래키 → student : 참조하는 테이블 / department : 참조 받는 테이블
- 참조 받는 속성 : 반드시 그 테이블의 primary key → 반드시 department 하나의 tuple이 특정되어야하기 때문
Data Dictionary
-
DBS가 내부적으로 관리하는 데이터 장소
-
meta data 관리
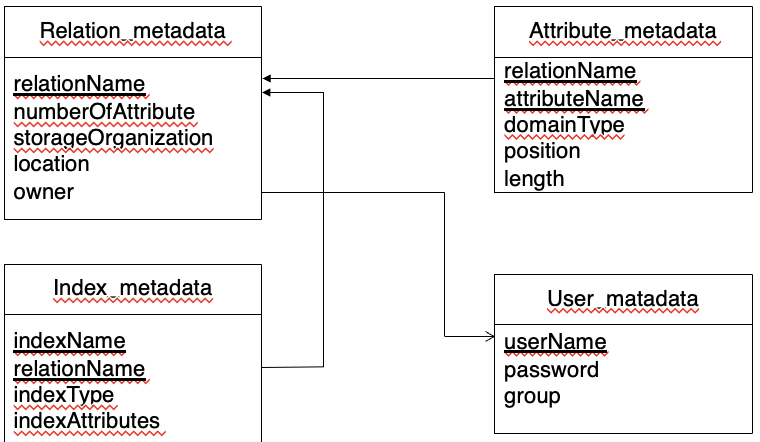
- relation 이름, 타입, 속성길이
- 제약 조건
- 사용자 계정 정보, 비밀번호
- physical file 조직 정보
-
사용자에게 투명한 데이터 사전 접근 허용
→ SQL 언어를 통해 Data Dictionary에 속하는 데이터 접근 가능
2.2 Sample University Database
스윽- 넘어감
2.3 Relational Algebra
Relational Algebra
- 관계 대수
- 관계형 데이터 모델의 일부
- 관계, 제약 사항에 대한 연산 제공
- 기본 연산 : 입력 / 삭제 / 갱신 / 검색
- (입력)하나 또는 두개의 관계 → (출력)새로운 관계 생성
- 관계 대수 연산의 중첩(composition) 허용
- 사용자에게 직접 지원 X → SQL 언어로 지원 관계 대수 = DBS 내부에서 사용되는 언어
- Procedural language 절차적 언어
- 질의 처리, 조건에 맞는 데이터 찾아 application에 전달 → user에게 전달
- 괄호에 묶여져있는 것부터 처리 (↔ 직설적)
- Basic operators

Select Operation
-
tuple 단위로 원하는 결과 선택하는 연산

-
Notation

- sigma, p = 선택 조건(selection predicate)
- p : 명제 논리(propositional logic) 표현 → ⋀(and), ⋁(or), ﹁(not)으로 연결 가능
Project Operation
-
속성 단위로 원하는 결과 선택하는 연산

-
중복된 tuple 제거 → set 기반이기 때문
-
Notation
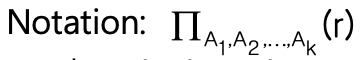
- A : 관계 속성명
Set Operation
- 집합 연산
- 관계 = tuple을 원소로 가지는 집합
- 제약 tuple의 속성 개수 동일! 대응되는 속성의 도메인 상호 호환적!
-
Union Operation
- 합집합

- Example
- 합집합
-
Set Difference Operation
- 차집합
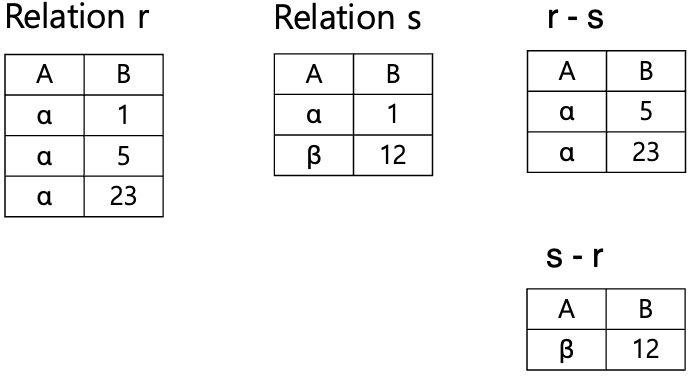
- commutative 하지 않다 : r - s ≠ s - r
- 차집합
Cartesian Product Operation
- 입력 관계에 속하는 tuple의 모든 가능한 조합 산출

- 연결 concatenation
- 동일속성 존재 시
- 자연 조인(natural join) 연산이 됨.
- rename 연산을 통해 동일한 속성이 없도록 해야함
- Arity(속성개수) : m + n tuple 개수 : x * y
Rename Operation
-
재명명 연산 : 단순히 관계, 속성 이름을 변경하는 연산

- ρ(rho)
-
E : 입력관계 / X : 관계명 / A : 속성명
-
관계명만 변경 시 : 속성명 생략 가능
-
Exercise
-
학생 테이블에서 CS학부이고 남자인 tuple 중에 name, GPA 속성만 선택

-
course 테이블에서 CS 학부이고 EE학부인 tuple 중 title 속성만 선택
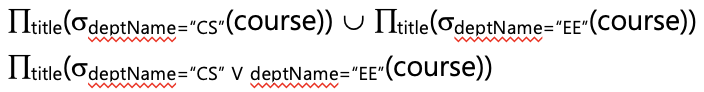
-
CS 학부이면서 동시에 EE학부인 tuple 중 title 속성만 선택 → wrong

→ 결과로 나오는 tuple은 항상 없다 (NULL)
→ Πtitle(σdeptName="CS"(course)) ⋂ Πtitle(σdeptName="EE"(course))
-
첫번째 학부 예산이 두번째 학부 예산보다 큰 학부 이름 쌍을 검색

- 카티시안곱 결과 : (deptName, chairman, building, budget, new-deptName, new-chairman, new-building, new-budget)
- 결과 : <EE, CS>, <EE, Media>, <CS, Media>
-
2023.09.18
2.4 Additional Relational Algebra
Assignment Operation
- 할당 연산
- 복잡한 질의문 작성 시 중간 결과 표현 임시 저장
- rename 과 함께 사용 : 중간 결과의 관계 및 속성 이름을 원하는 것으로
- ←
Set intersection Operation
- 교집합
-
2회 차집합 연산 적용으로 표현 가능

-
- 관계 대수 집합 연산자 특징 동일 1) 속성 개수 동일 2) 대응되는 속성의 데이터 타입 상호호환 3) tuple을 하나의 원소로 취급
join Operation
- 조인
- 타 관계 대수 연산에 비해 시간이 많이 소요되는 비싼 연산
- 조인 연산 중 가장 흔하게 사용되는 조인 : 자연 조인
- 결합하는 방식에 따라 : Inner Join, Outer Join, Natural Join
- Inner join 내부조인
- 종류
- theta-join 세타 조인 : 가장 일반적인 조인 연산
- equi-join 동등 조인 : 세타 조인 중 조인 조건이 동증 조건만으로 구성
- natural join 자연 조인 : 동등 조인 중 조인 조건 속성이 결과에 한 번만
- 조인 조건 만족 X tuple → 조인 결과에서 배제
- 종류
- Outer join 외부 조인
- 조인 조건 만족 X → 결과 관계에 포함
- 좀 더 많은 tuple 정보를 결과 관계에 유지 가능
- null values 사용
Natural join Operation
-
자연 조인
1) 카티시안곱 수행
2) 조인 조건을 이용하여 선택 연산 수행
3) 조인 조건에 언급된 속성 이용하여 투영연산 수행
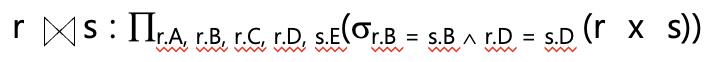
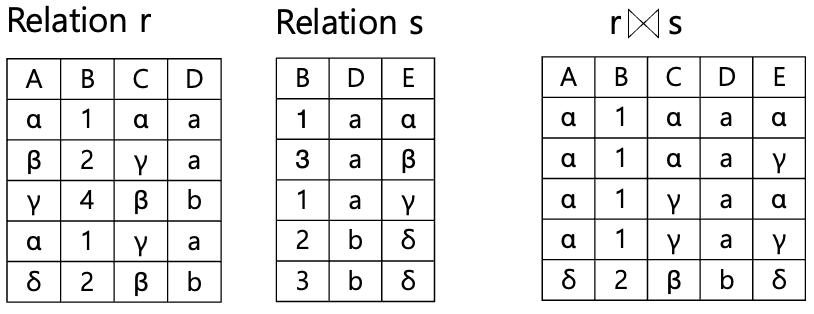
- 조인 속성 : 같은 이름의 속성 (ex. B, D)
- 특정 속성만 조인 조건으로 사용하려면 → rename 하거나 조인 조건 명시하기
-
Example > 2020년 가을 학기에 강의한 교수명과 교수가 강의한 과목명 검색

- teaches : 2020년 가을에 개설된 과목 검색 (교수번호, 과목번호)
- professor : 교수명 검색 (교수번호, 교수명)
- course : 과목명 (교수번호, 과목명) → deptName 속성 이름을 변경하기 위해 rename 연산
-
결합성(associative) & 교환성(commutative)
- 질의어 최적화
- 결합성

- 교환성

Theta join/Equi join Operation
-
theta join : 조건문에 의한 조인
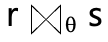

- theta라는 조건을 만족시키는 tuple만 가져옴 cf. 카티시안곱 수행 : 가능한 모든 tuple 다 찾아냄
- theta라는 조건을 만족시키는 tuple만 가져옴 cf. 카티시안곱 수행 : 가능한 모든 tuple 다 찾아냄
-
Example>
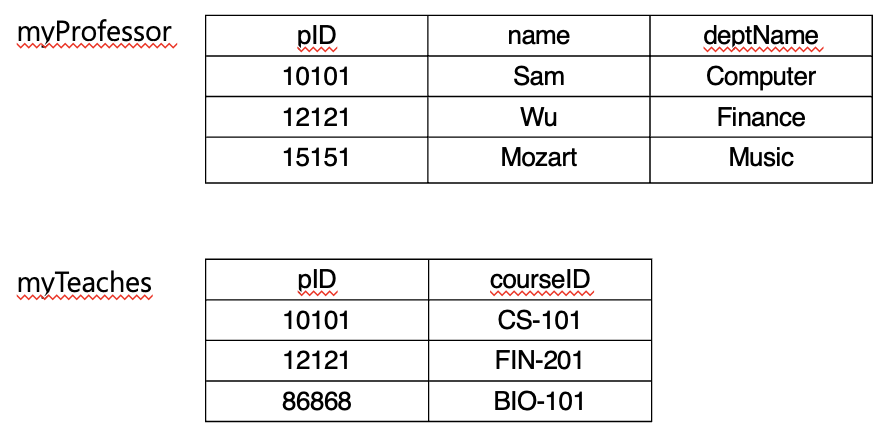

- 이름 모호성 해결 : “관계명.속성명”
-
Equi join 동등 조인
-
조인 조건 모두 동등조건을 가지는 경우
-
입력 관계의 모든 속성이 결과 테이블에 속함
-
반드시 동일한 내용을 가지는 속성이 두 번 표시됨
→ 속성명은 재명명되어 구분→ 중복되는 정보 제거 : 자연 조인
-
Outer join Operation
-
Natural Left Outer Join
- 자연 왼쪽 외부 조인

- 왼쪽에 오는 입력 관계의 모든 tuple이 결과 관계에 표시
- join 되는 값 존재 X → null 값 사용
- 자연 왼쪽 외부 조인
-
Natural Right Outer Join
- 자연 오른쪽 외부 조인
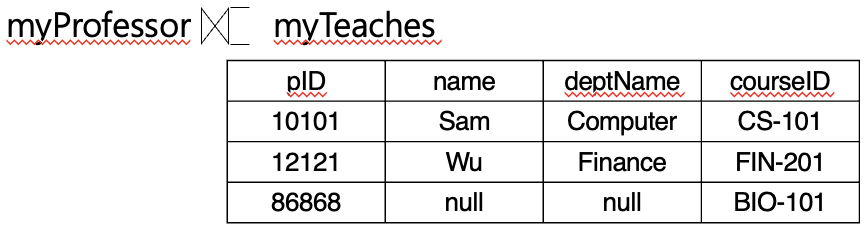
- 자연 오른쪽 외부 조인
-
Full Outer Join
- 완전 외부 조인
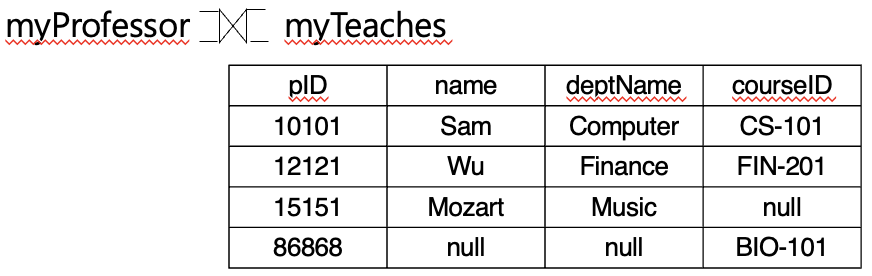
- 오른쪽 외부 조인 연산 + 왼쪽 외부 조인 연산
- 두 입력 관계의 모든 tuple이 결과에 표시
- 완전 외부 조인
Division Operation
-
나눔
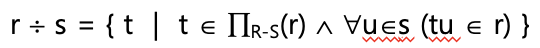
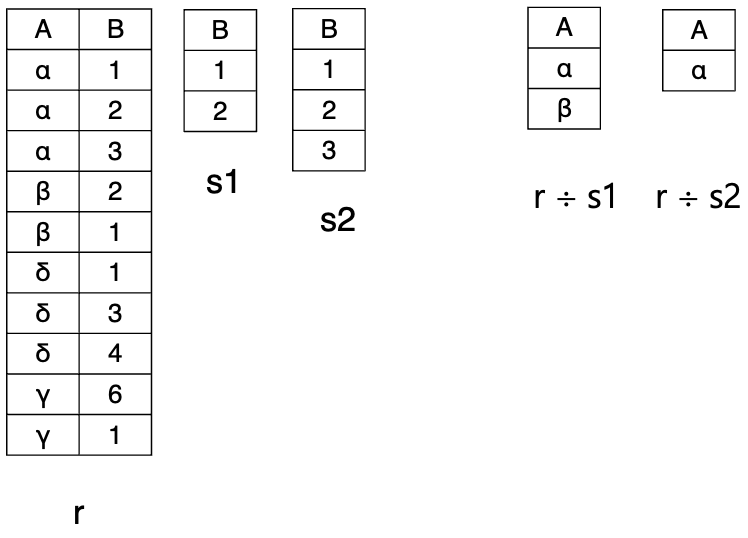
-
입력 관계 2개
→ 공통 이름을 가지는 속성이 존재해야함.
-
결과 관계 : 공통 속성이 제거된 속성
→ S 관계의 공통 속성에 속하는 모든 tuple을 가진 R 관계 tuple
-
universal quantifier(전체정량자, ‘모든’조건)에 대응되는 질의 구현
- ex. 모든 CS 학과 과목을 수강한 학생 학번
- 전체정량자 → 나눔 / 존재정량자(existential) → 조인
-
SQL : 나눔 연산 직접 지원 X → 차집합 연산 활용(간접 지원)
-
기본 연산으로 표현 가능
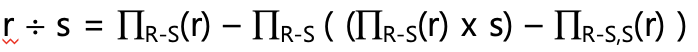
요약
기본 관계 대수 기본 대수를 이용하여 대치 가능한 확장 관계 대수

2023.09.21
[Exercise] Bank Schema
-
$1200이 넘는 amount를 가진 모든 loan 찾기 : select
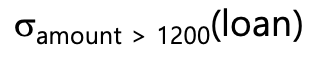
-
$1200이 넘는 amount 중 loanNumber 찾기 : select, project

-
loan 혹은 account를 가진 모든 customer의 이름 찾기 : union, project

-
Seoul branch에서 loan을 가진 모든 customer의 이름 찾기


-
Seoul branch에서 loan을 가졌지만 어느 다른 bank에서도 account를 가지지 않은 모든 customer의 이름 찾

-
가장 큰 account balance 찾기
-
가장 크지 않은 balance 찾아서 차집합 시키기
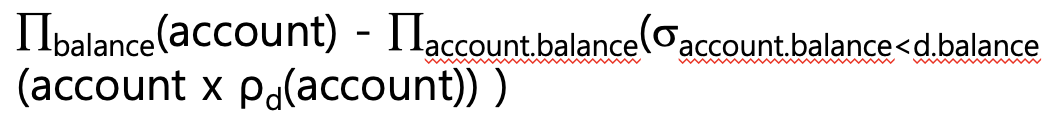
-
