[Algorithm] Stack/Queue

이 포스팅에서 소개할 내용은 다음과 같습니다.

1. Stack과 Queue란 무엇인가.

• Stack과 Queue는 자료를 저장하는 순서리스트(ordered list)입니다.

• Stack
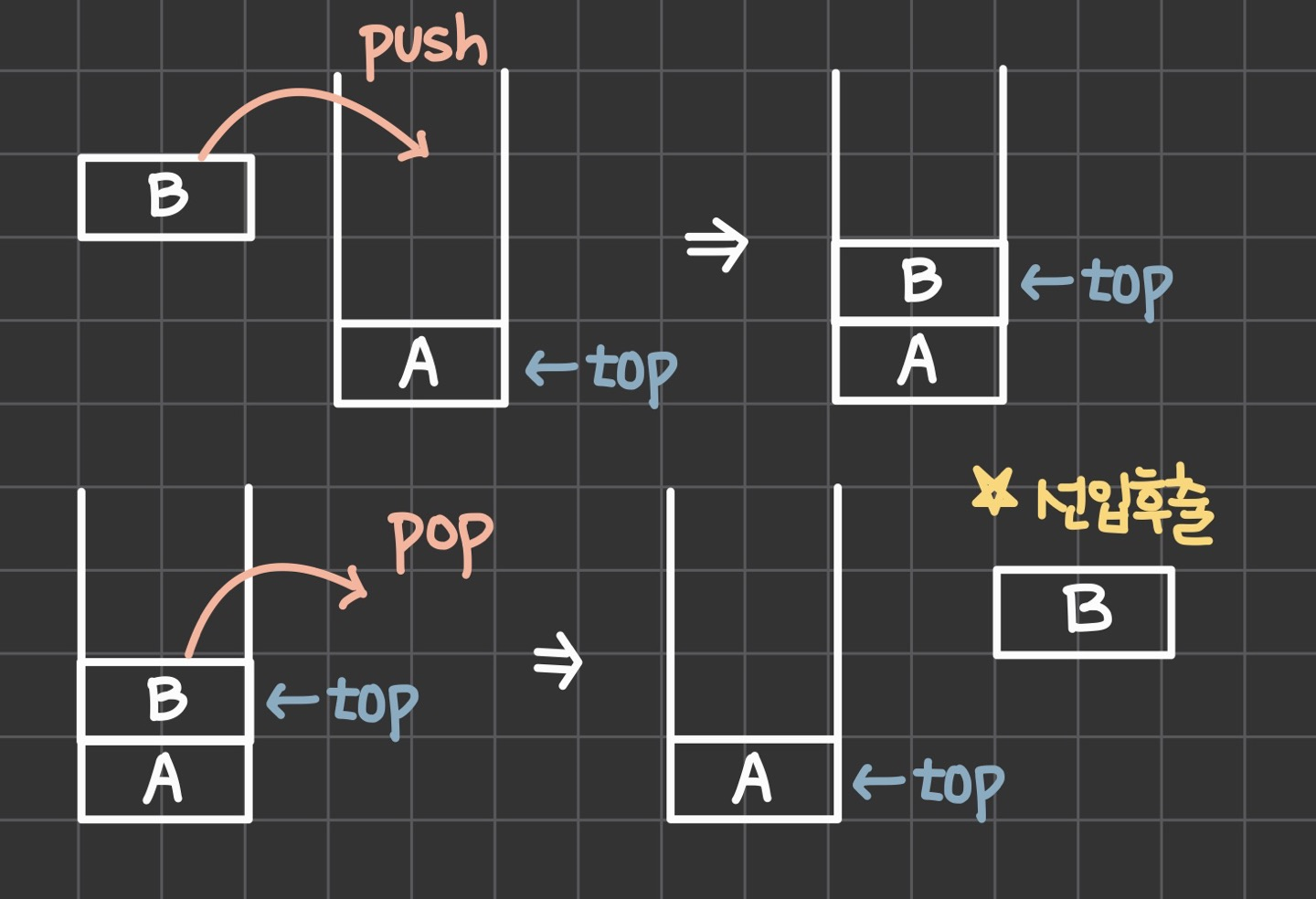
  - top : 스택의 최상위 원소
  - top = -1 : 공백 스택을 의미함.
  - top이라고 하는 한쪽 끝에서 삽입(Push)과 삭제(Pop) 모두 수행
  - 선입후출, 후입선출(LIFO, Last-In-First-Out)
  - Peak : top에 있는 원소를 삭제하지 않고 반환
  - 시스템 스택 구조 (운영체제 시간에 자세히 배움)

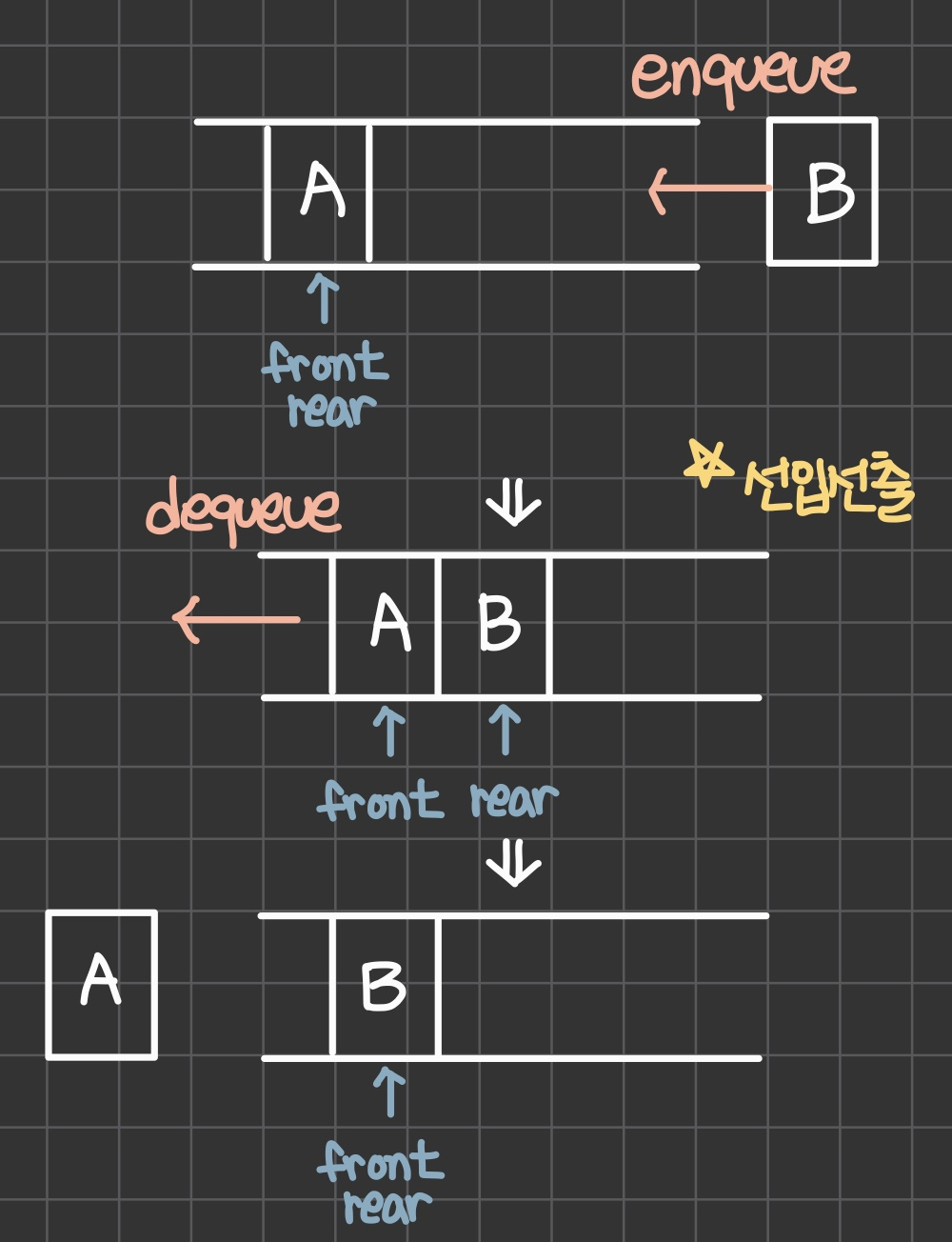
• Queue
  - rear : 새로운 원소가 삽입되는 끝
  - front : 원소가 삭제되는 끝
  - 선입선출, 후입후출(FIFO, First-In-First-Out)
  - Enqueue(삽입) : queue[rear] 바로 뒤에 원소 삽입
  -> 배열 크기 조절시간을 제외하면, 시간 복잡도 : Θ(1)
  - Dequeue(삭제) : queue[0], 즉 queue[front]에 있는 원소 삭제
  -> 삭제할 때마다 나머지 원소들을 왼쪽으로 이동시키는 작업 필요
  -> queue가 n개의 원소를 가질 때, 삭제 시 시간 복잡도 : Θ(n)
  - 왼쪽으로 이동시키는 작업을 안 하려면 ?
  -> 원형 큐(Circular queue) 이용! 시간 복잡도 : Θ(1)
  -> 불필요한 공간이 생김
  - 불필요한 공간없이 공간 전부를 사용하려면 ?
  -> laspOp변수 사용 (수행된 마지막 연산을 기록해두는 방법)
  -> 메모리 한 칸을 더 사용할 수 있다는 장점이 있지만, Push, Pop이 빈번하게 사용될 경우 lastOp에 계속 저장해줘야하기에 시간 복잡도↑
  

2. 그림으로 이해하는 Stack

3. 코드로 이해하는 Stack

#include <iostream>

using namespace std;

template<class T>
class Stack {
    private:
        T *stack;       //스택 원소를 위한 배열
        int top;        //톱 원소의 위치
        int capacity;   //스택 배열의 크기
    
    public:
        Stack () {
            top = -1;
            capacity = 10;
            stack = new T[10];
        }

        void Push (T input) {   //원소 삽입하기
            if (top != capacity)
                stack[++top] = input;    
            else {                      //공간최적화를 위한 공간할당
                capacity *= 2;
                T *newterm = stack;
                stack = new T[capacity];
                stack = newterm;
                stack[++top] = input;
            }
        }

        void Pop() {            //top에 있는 원소 삭제하기
            top--;
        }
        T Peak() {              //삭제하지 않고 top에 있는 원소 뽑아오기
            return stack[top];
        }

        void allPrint() {
            for (int i = 0; i <= top; i++) {
                cout << stack[i] << endl;
            }
        }
};

int main() {
    cout << "스택 활용 시작!============================" << endl;
    int menu = 0;
    Stack <int>myStack;
    int tmp;

    while(1) {
        cout << "메뉴 : Push(1번), Pop(2번), Peak(3번), 스택출력(4번), 끝내기(0번) >> ";
        cin >> menu;
        switch(menu) {
            case 0:
                return 0;
            case 1:
                cout << "Push할 정수값을 입력하세요 >>";
                cin >> tmp;
                myStack.Push(tmp);
                break;
            case 2:
                myStack.Pop();
                break;
            case 3:
                cout << myStack.Peak() << endl;
                break;
            case 4:
                myStack.allPrint();
                break;
        }
    }
}

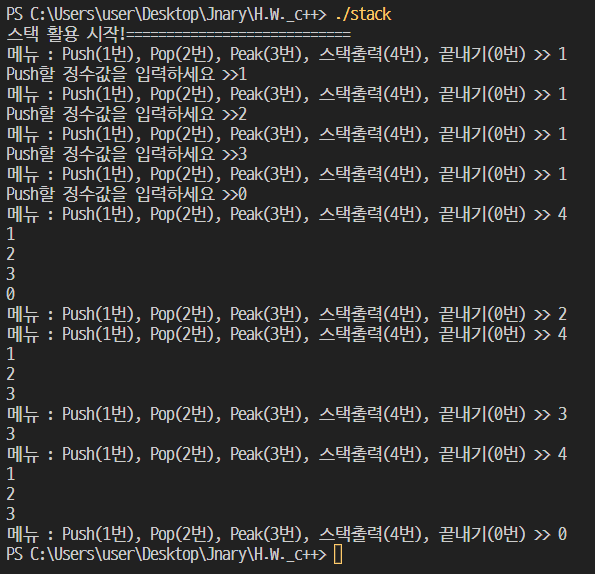
출력결과는 다음과 같습니다.

4. 그림으로 이해하는 Queue

5. 코드로 이해하는 Queue