서포트 벡터 머신(Support Vector Machine)
→ 서포트 벡터 머신은 매우 강력하고 선형이나 비선형 분류, 회귀, 이상치 탐색에 사용할 수 있는 다목적 머신러닝 모델
- 결정 경계를 기준으로 데이터를 분류하는 것
⬜️ 선형 SVM 분류
→ SVM 분류기를 클래스 사이에 가장 폭이 넓은 도로를 찾는 것으로 생각할 수 있음
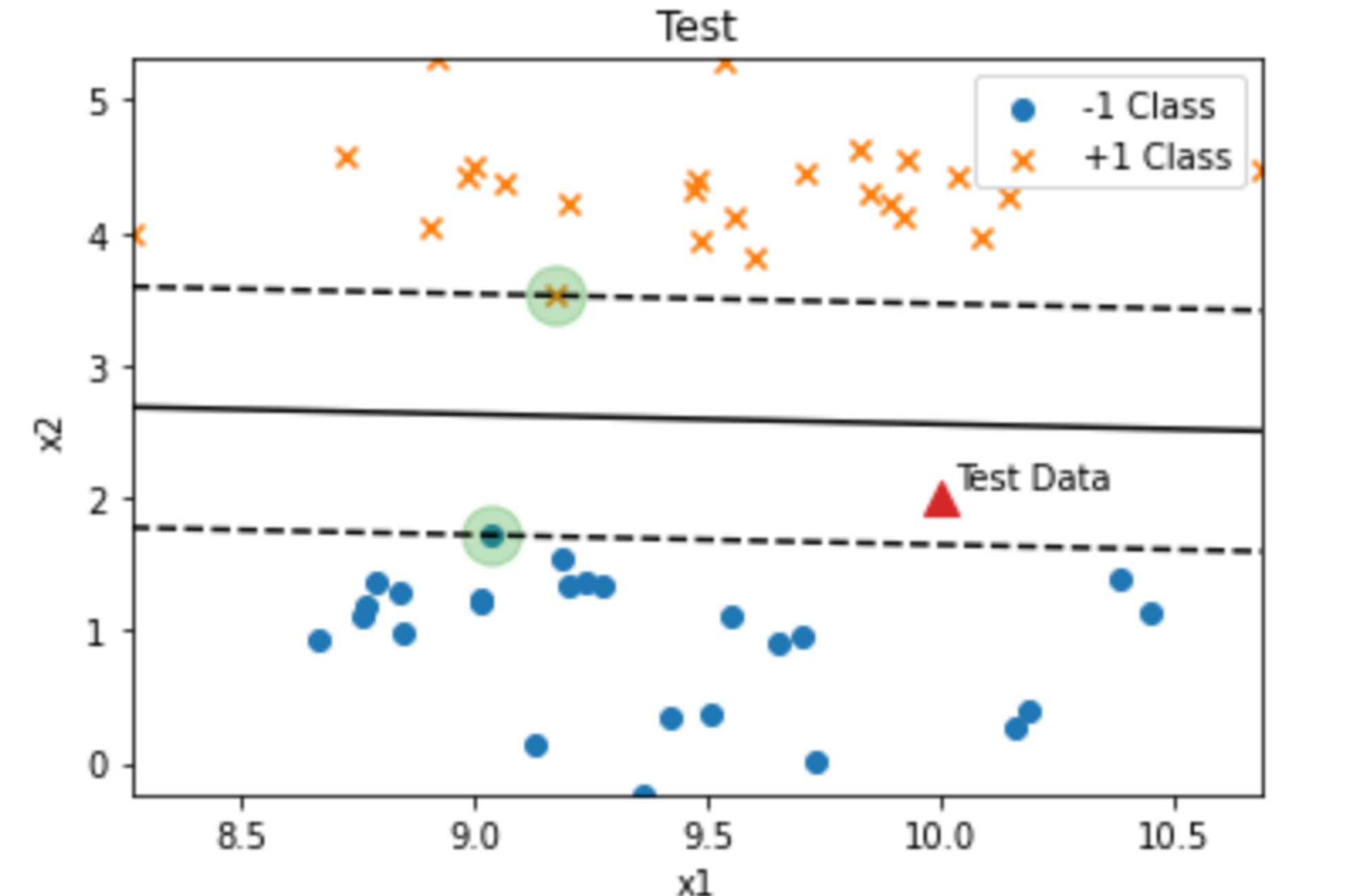
서로 다른 클래스 두 개 사이에서 구분이 되게 결정경계를 기준으로 나누어 준다.
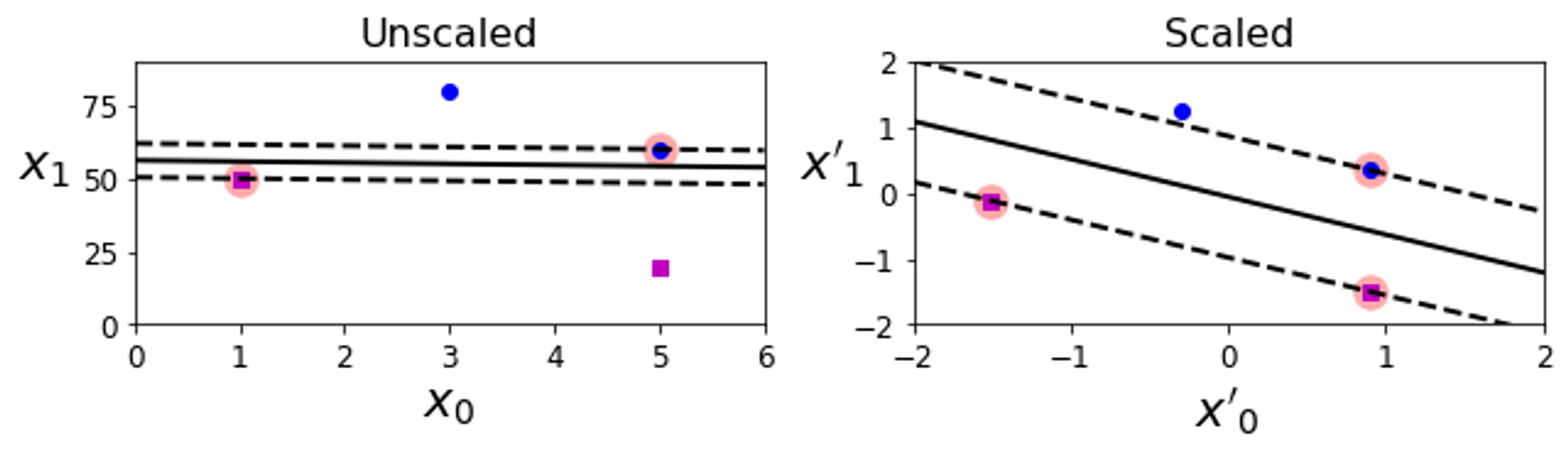
→ 특성 스케일에 따른 민감성. 왼쪽 그래프는 수직축의 스케일이 훨씬 커서 가장 넓은 도로가 거의 수평에 가깝게 된다. 이러한 특성을 조절하여 스케일을 수평축과 비슷하게 조정하면 오른쪽 그래프에서처럼 결정 경계가 훨씬 좋아진다
⬜️ 소프트 마진 분류
- 모든 샘플이 도로 바깥쪽에 올바르게 분류되어 있다면 하드 마진 분류라고 한다.
하드 마진 분류에는 두 가지 문제점이 존재한다.
1. 데이터가 선형적으로 구분될 수 있어야 제대로 작동함
2. 이상치에 민감함
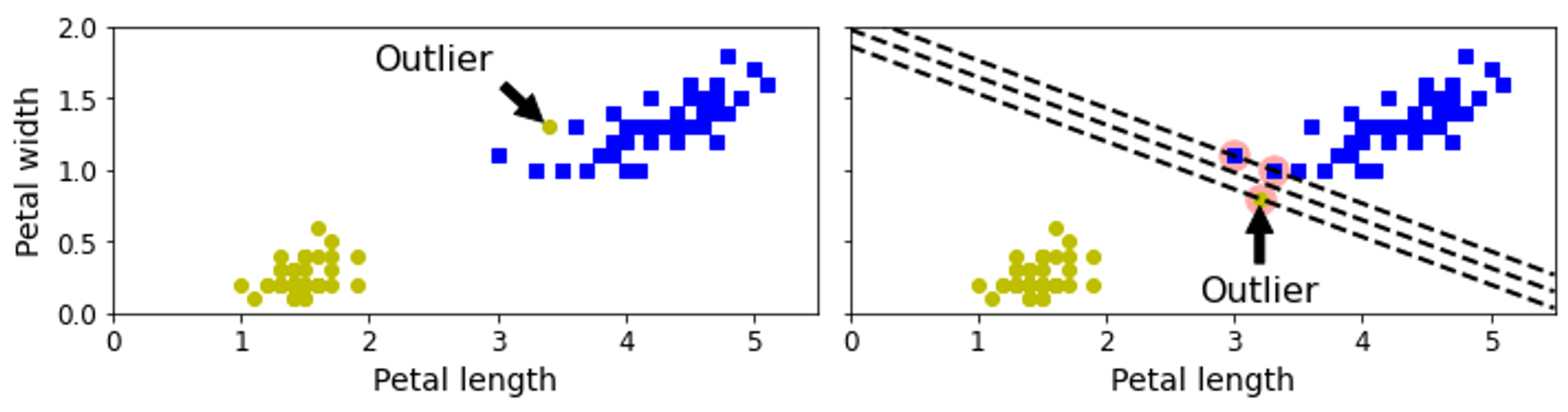
→ 데이터에 이상치가 하나 있는 경우 왼쪽 그래프에서는 하드 마진을 찾을 수 없음
오른쪽 그래프의 결정경계에서는 일반화가 잘 되지 않음
‼️ 이런문제를 해결하기 위해 유연한 모델이 필요 !
이에 따라 등장한 모델이 소프트 마진 분류 이다.
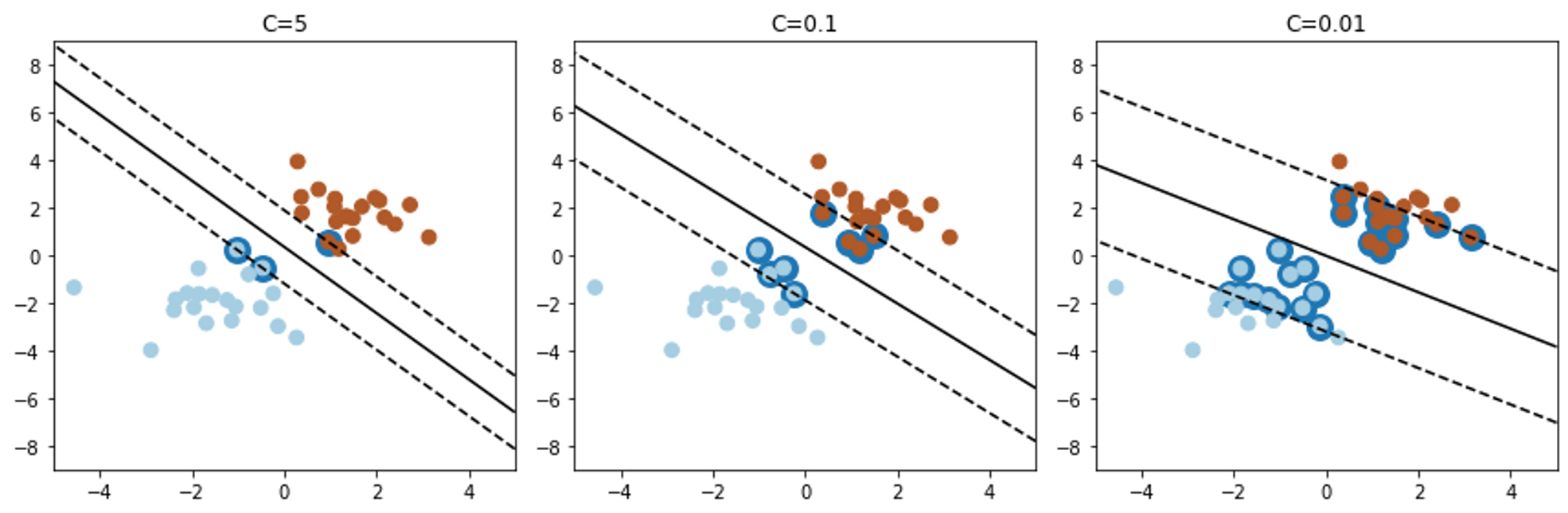
‼️ 사이킷런의 SVM 모델을 만들 대 여러 하이퍼 파라미터를 지정할 수 있다. C 는 이 하이퍼 파라미터 중 하나이다. C의 값을 변경해가며 SVM을 돌렸을 때 결과 값은 아래와 같다.
💡 SVM 모델이 과적합이라면 C를 감소시켜 모델을 규제 할 수 있다.
C 값이 클수록 하드 마진, 작을수록 소프트 마진에 가깝다.
C 값이 너무 크면 오버피팅, 너무 작으면 언더피팅에 가깝다.
🟨 사이킷런 SVM 주요 파라미터
| 파라미터 | default | 설명 |
|---|---|---|
| C | 1.0 | 오류를 얼마나 허용할 것인지 → 클수록 하드 마진, 작을수록 소프트 마진에 가까움 |
| kernel | 'rbf’(가우시안 커널) | 'linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ |
| degree | 3 | 다항식 커널의 차수 결정 |
| gamma | 'scale’ | 결정 경계를 얼마나 유연하게 그릴지 결정 클수록 오버피팅 발생 가능성이 높아짐 |
| coef | 0.0 | 다항식 커널에 있는 상수항 r |
선형 데이터 셋의 경우 ‘linear’, 비선형 데이터 셋은 ‘poly’, ‘rbf’ 커널을 주로 이용한다. 다항식 커널은 degree로 차수를 지정해줘야 하며 rbf 커널이라면 gamma 와 C 값 조정이 필수적이다!
⬜️ 비선형 SVM 분류
선형 SVM 분류기가 효율적이지만, 선형적으로 분류할 수 없는 데이터 셋이 많다.
비선형 데이터셋을 다루는 방법은 다항 특성과 같은 특성을 더 추가하는 것이다.
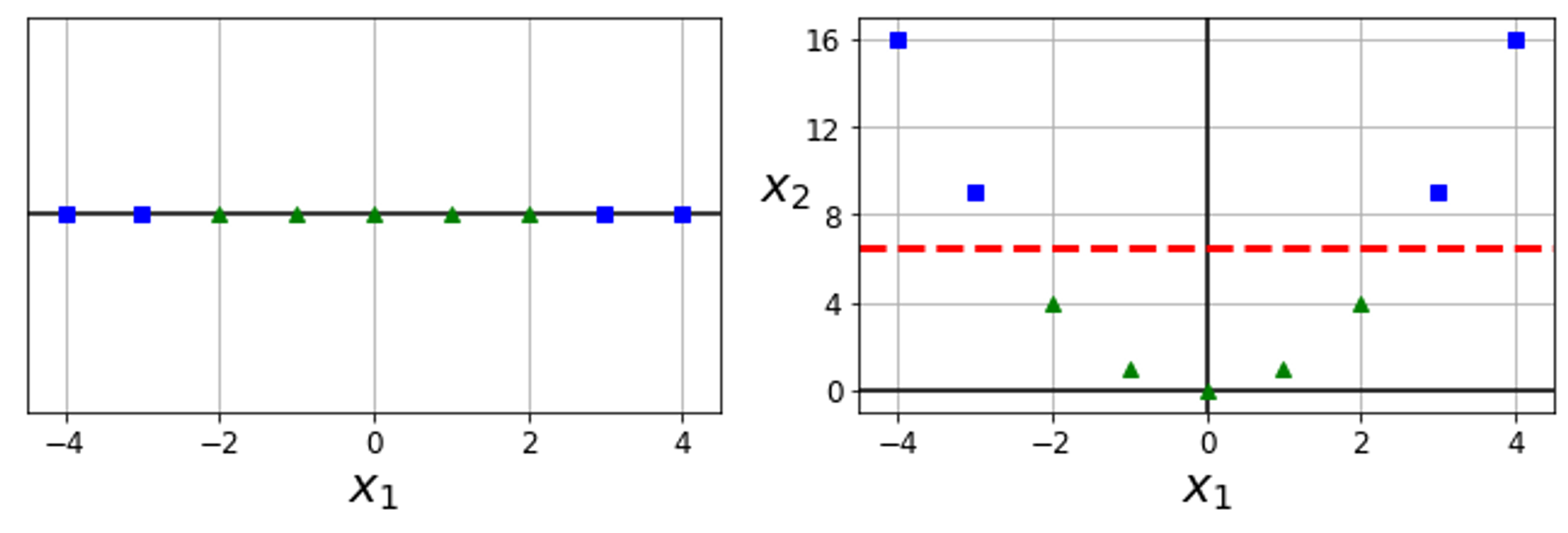
→ 왼쪽 그래프에서는 하나의 특성만 고려하여 선형 분류로 데이터를 분류할 수 없다 .
하지만 특성을 추가하여 다항식으로 나타내면 선형으로 분류가 가능하다.
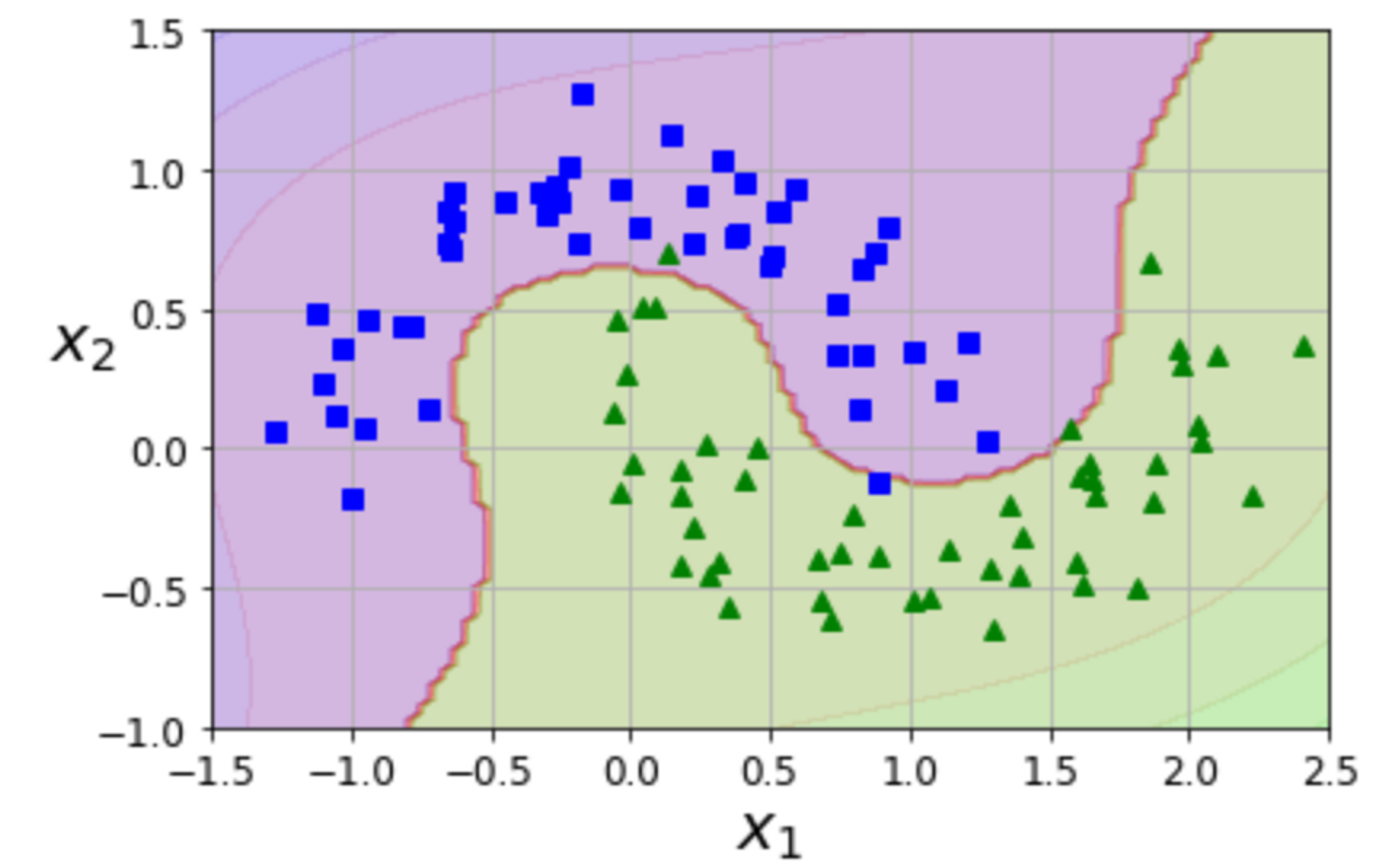
→ 사이킷런에서 구현하고자 StandardScaler, LinearSVC 를 연결하여 Pipeline을 만들었다. 이를 적용하여 두 개의 마주보는 데이터들을 다항 특성을 사용하여 분류하였다.
⬜️ 다항식 커널
낮은 차수의 다항식은 매우 복잡한 데이터셋을 잘 표현하지 못하고 높은 차수의 다항식은 너무 많은 특성을 추가하여 모델을 느리게 만든다.
→ SVM에서 커널 트릭을 적용할 수 있다.
커널 트릭이란 실제로는 특성을 추가하지 않으면서도 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있다.
3차 다항식 커널을 사용하여 분류기를 훈련
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler",StandardScaler()),
("svm_clf",SVC(kernel = "poly",degree = 3, coef0 = 1,C = 5))
])
poly_kernel_svm_clf.fit(X,y)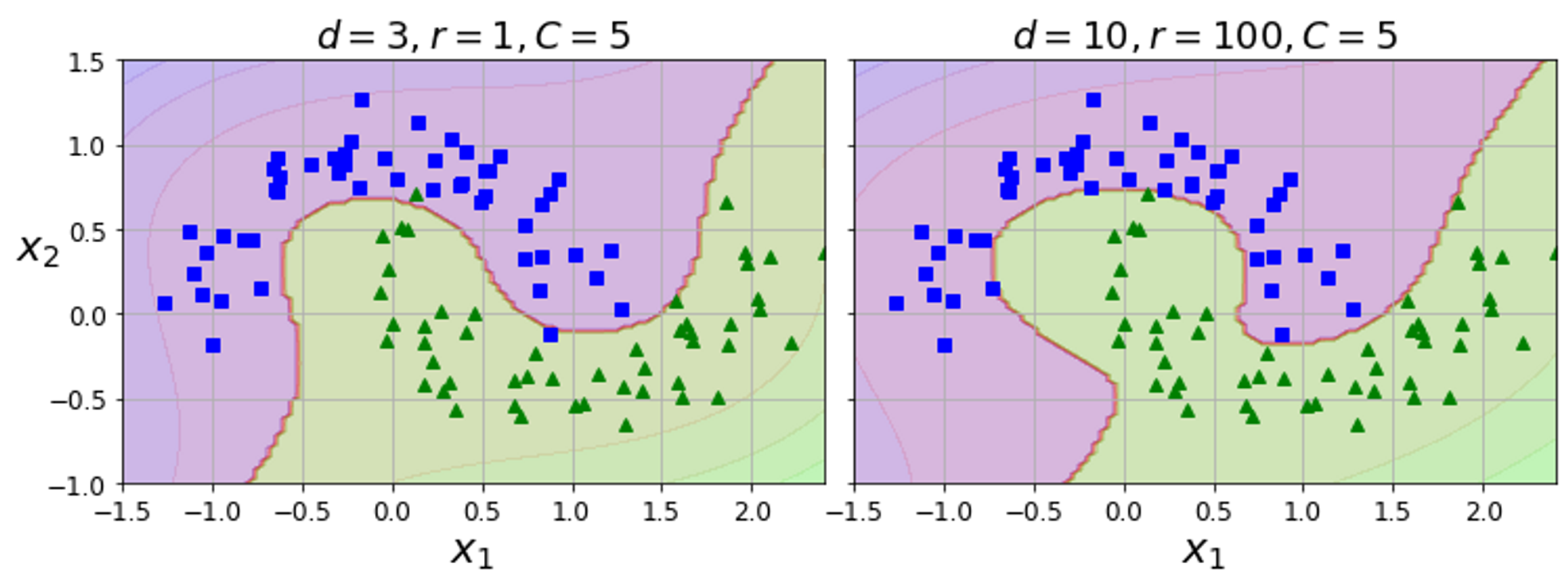
⬜️ 가우시안 RBF 커널
rbf_kernel_svm_clf = Pipeline([
("scaler",StandaradScaler()),
("svm_clf",SVC(kernel = "rbf",gamma = 5,C = 0.001))
])
rbf_kernel_svm_clf.fit(X,y)
→ 가우시안 RBF 커널을 사용한 SVC 모델이다.
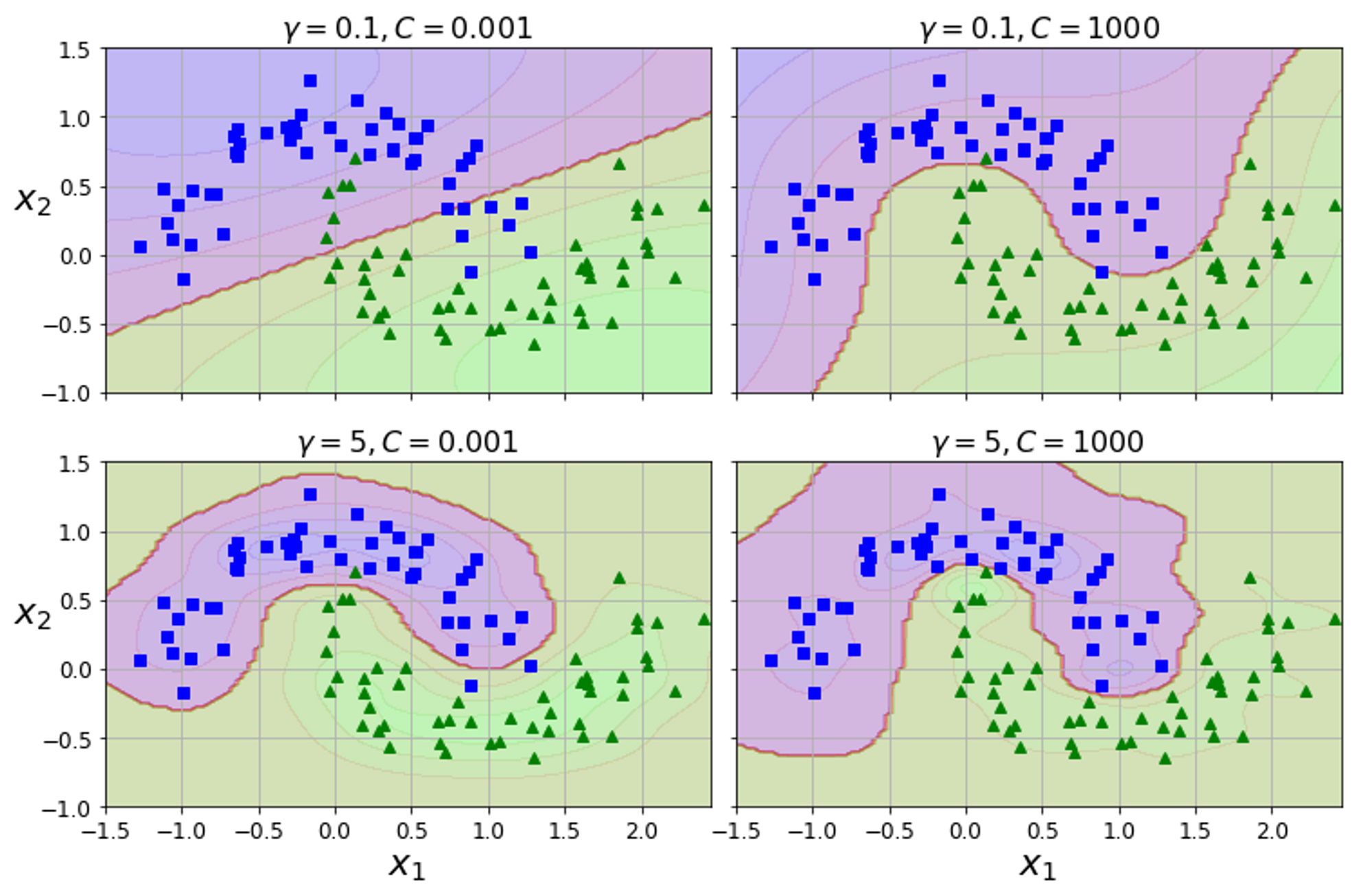
→ 위 코드에서 gamma와 C 값을 바꾸워 모델 훈련 시킨 결과이다. gamma 값이 커지면 보라색 영역이 좁아지고 작으면 더 단순하고 부드러워진다.
하지만 gamma값이 너무 크면 오버 피팅이 발생할 수 있다!
🤔 여러가지 커널 중 어떤 것을 사용해야 할까?
→ 경험적으로 언제나 선형커널을 먼저 시도하는 것이 순서! LinearSVC 가 SVC(kernel=”linear”) 보다 훨씬 빠르다는 것을 기억해야 함 . 하지만 데이터의 구조에 특화된 커널이 있다면 해당 커널을 테스트하는 것이 이상적이다.
⬜️ SVM 회귀
→ SVM은 분류 뿐만 아니라 선형, 비선형 회귀에도 적용할 수 있다.
일정한 margin 오류 안에서 두 클래스 간의 도로 폭이 가능한 최대가 되도록 하는 대신, SVM 회귀는 margin 오류 안에서 도로가 가능한 많은 샘플이 들어가도록 학습
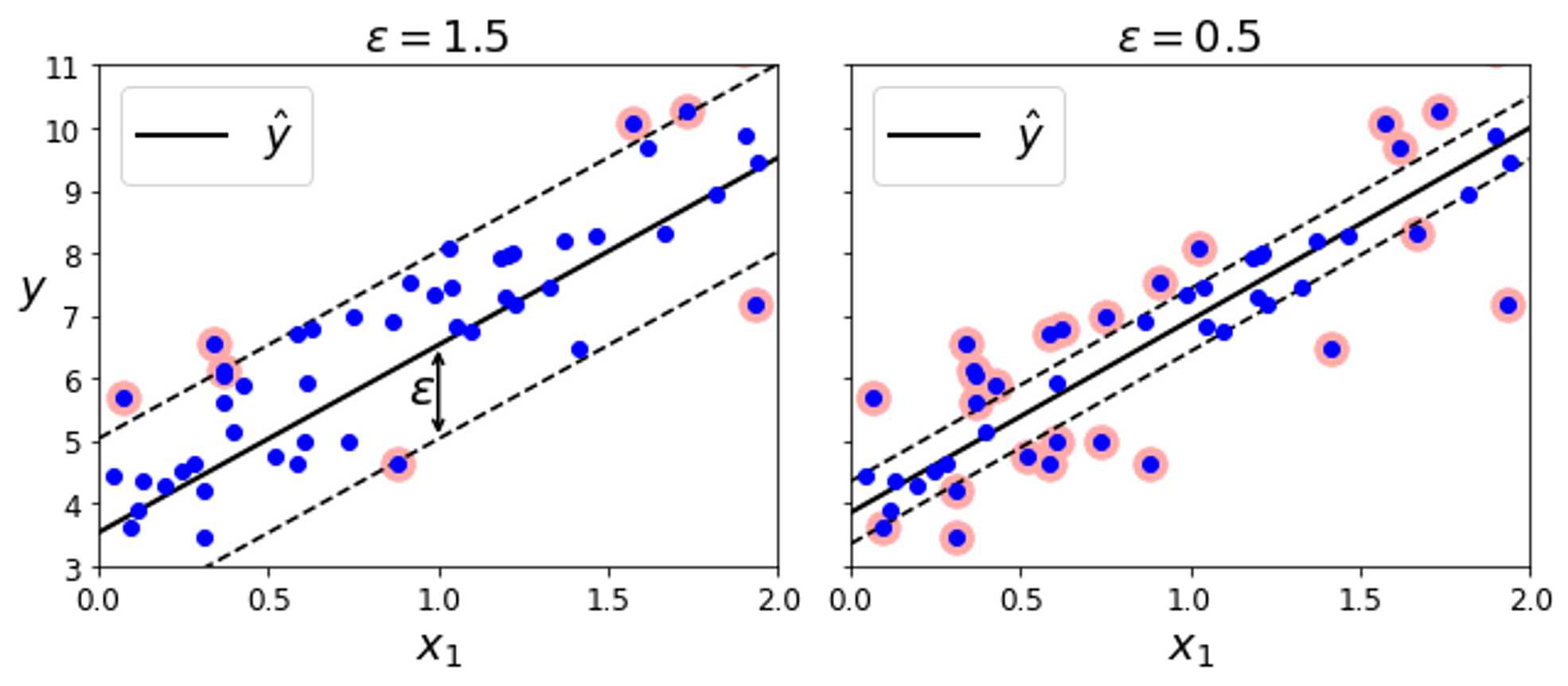
→ 무작위로 생성한 선형 데이터 셋에 훈련시킨 두 개의 선형 SVM 회귀 모델
sklearn을 이용한 svm 회귀 모델 학습 코드
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon = 1.5)
svm_reg.fit(X,y)⬜️ 비선형 SVM 회귀
비선형 회귀 작업을 위하여 커널 SVM 모델을 사용한다.
비선형 SVM 회귀모델 학습 코드
from sklearn.svm import SVR
np.random.seed(42)
m = 100
X = 2*np.random.rand(m,1) -1
y = (0.2 +0.1*X +0.5*X**2 + np.random.randn(m,1)/10).ravel()
svm_poly_reg1 = SVR(kernel = "poly", degree = 2, C = 100, epsilon = 0.1, gamma = "scale")
svm_poly_reg2 = SVR(kernel = "poly",degree = 2, C = 0.005 , epsilon = 0.1 , gamma = "scale")
svm_poly_reg1.fit(X,y)
svm_poly_reg2.fit(X,y)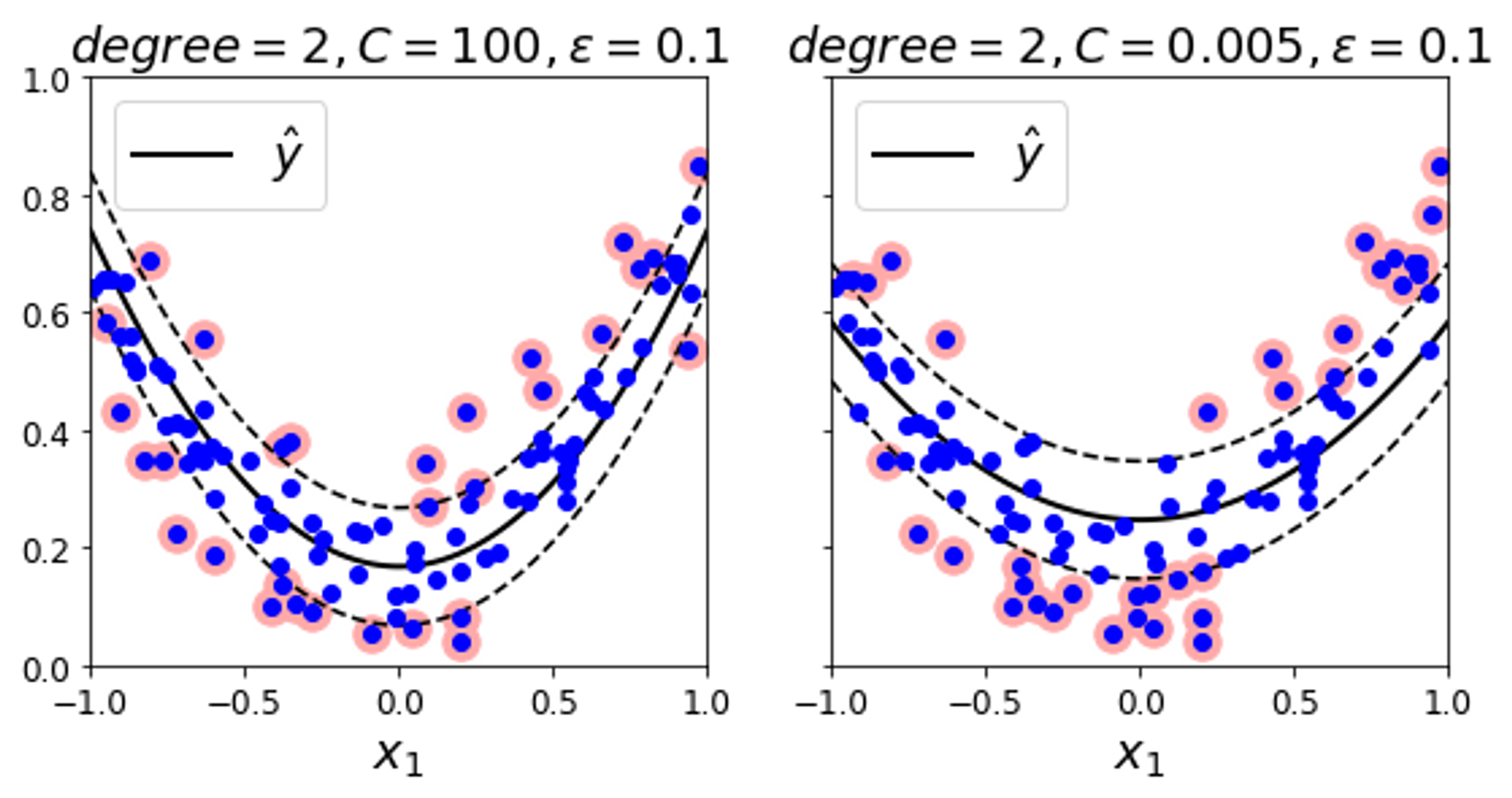
→ 임의의 2차 방정식 훈련 세트에 2차 다항 커널을 사용한 SVM 회귀 이다. 왼쪽 그래프는 규제가 거의 없고, 오른쪽 그래프는 규제가 많다
참조
