[머신러닝] 선형 회귀 분석 (Linear Regression)

민정·2023년 3월 12일

데이터분석 머신러닝 회귀

머신러닝

목록 보기

6/9

🟡 회귀 분석이란?

→ 결과를 일으키는 원인을 찾아가는 과정

종속 변수 : 실험에서 결과에 해당하는 값, 1차 방정식으로 이해하면 y 값에 해당
독립 변수 : 원인에 해당하는 개념

⬜️ 회귀 분석의 목적

→ 과거 현상이 어떤 원인 때문에 발생하였는지 밝혀내고 이해하는데 사용 한다. 예시로 기본 금리 상승과 이자율 상승은 어떤 관계를 가지고 있는지를 파악할 때 사용할 수 있다. 따라서 모델이 갖고 있는 설명력이 중요

→ 과거의 데이터를 기반으로 모델을 형성하여, 미래의 값을 예측하는데 사용

→ 통계 해석학에서 인과관계를 측정하고, 그것이 맞는지 증명하는데 회귀 분석을 활용한다. 인과 관계를 측정하고 추적하는 기능 수행

⬜️ 선형 회귀 분석 해석 순서

✔️ 유의성 검증 - Significance

계산한 x의 계수가 실제로 일반화할 수 있는 수치인지 확인하는 과정
계수의 p-value 가 유의한지 검증하는 것으로 진행
사회과학에서는 0.05보다 작으면 유의한 계수로 해석함

✔️ 방향성 확인 - Direction

내가 세운 가설대로 계수의 방향성이 나오는지 확인하는 과정
예를 들어 계수의 값이 양수가 나올 것이라는 예측을 하였을 때, 그 방향대로 나오는지 확인

✔️ 효과의 크기 - Effect Size

계수 자체의 절댓값을 측정하는 것
유의하더라도 만약 그 효과 크기가 너무나도 작다면 , 그 결과를 반영하지 않을 수도 있다.

✔️ 모델 적합성 - Model Fitting

통계 모델이 데이터 셋을 전체적으로 얼마나 잘 설명했는가를 나타내는 것
주어진 데이터 셋을 모델이 오차 범위내에서 설명을 했다면 적합한 모델이라고 판단

🤔 선형회귀(Linear Regression)은 널리 사용되는 회귀 알고리즘이다.

선형 회귀는 종속 변수 y 와 하나 이상의 독립 변수 x 와 선형 상관 관계를 모델링하는 방법이다

독립변수 x가 하나라면 단순 선형 회귀, 2개 이상이면 다중 선형 회귀이다.

🟨 단순 선형 회귀 모델의 예측 식

\hat{\boldsymbol{\mathbf{y}}} ={\theta_0} +{\theta_1}{\mathbf{x}}

단순 선형 회귀는 독립 변수 x에 곱해지는 가중치와, 상수항에 해당하는 편향 (bias)값을 통하여 예측한다. 단순 선형 회귀모델 훈련을 통하여 적절한 값을 찾는다. 그래프의 형태는 직선으로 나타난다.

🟨 다중 선형 회귀 모델의 예측식

\hat{\boldsymbol{\mathbf{y}}} ={\theta_0} +{\theta_1}{\mathbf{x_1}}+{\theta_2}{\mathbf{x_2}}+ ... +{\theta_n}{\mathbf{x_n}}

다중 선형 회귀는 여러 독립 변수에 의해 영향을 받는 경우이다. 만약 2개의 독립변수면 그래프는 평면으로 나타날 것이다. n은 특성의 수, xi는 i번째 특성 값을 나타낸다.

🟡 정규 방정식

비용함수를 최소화하는 theta 값을 찾기 위하여 정규방정식을 사용한다.

정규 방정식

\hat{\boldsymbol{\theta}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}

import numpy as np

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)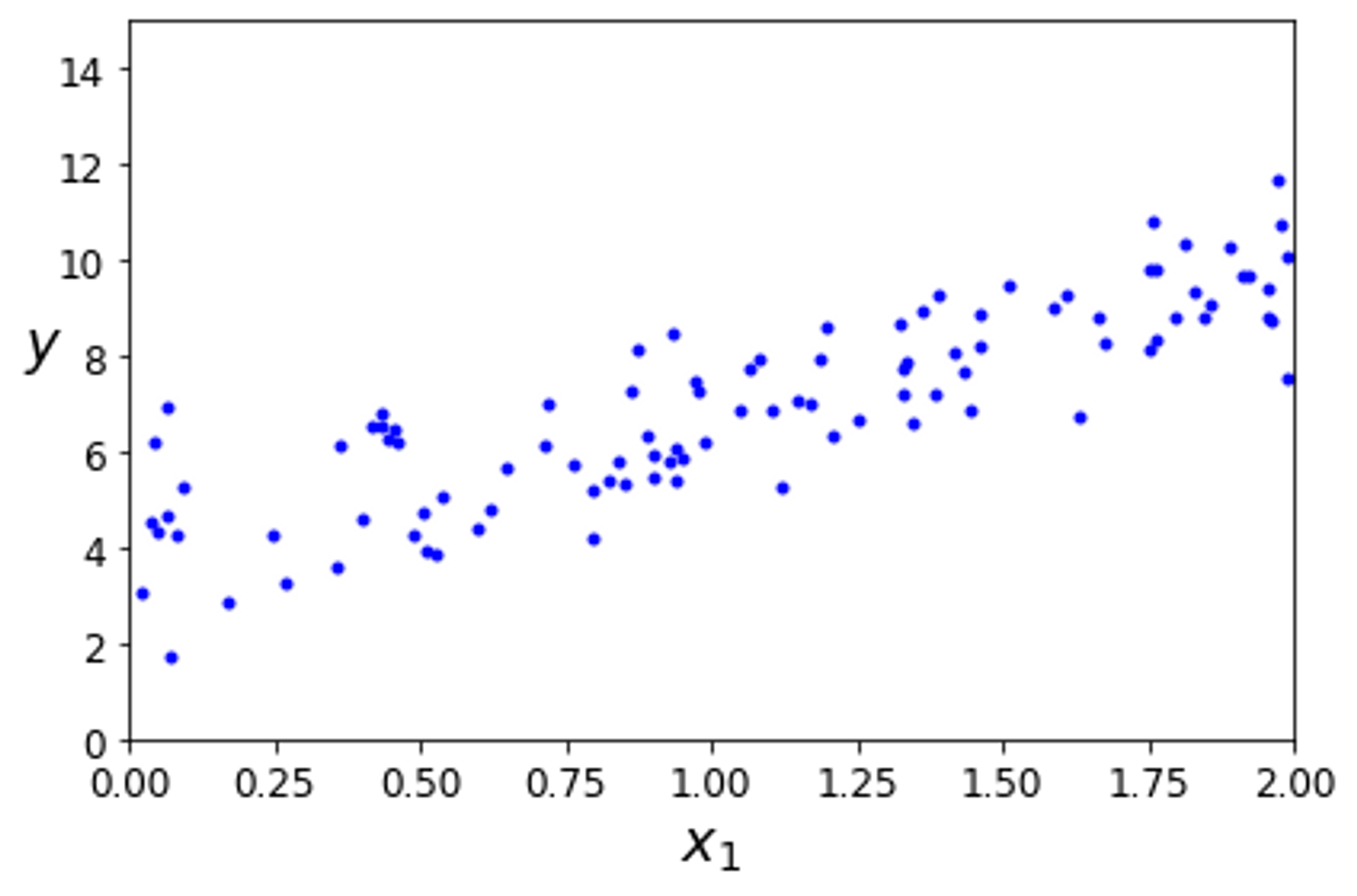

→ 임의로 선형 모형의 데이터를 생성하였다

정규 방정식을 사용하여 $\hat{\boldsymbol{\theta}}$ 을 계산하여 보았다.

X_b = np.c_[np.ones((100,1)),X]
theta_hat = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

정규 방정식으로 계산한 값을 확인하면

array([[3.86618727],[2.92732447]])

의 결과가 나왔다. 매우 비슷하지만 잡음의 존재로 원래 함수의 파라미터(4,3) 를 아주 정확하게 예측하진 못하였다.

$\hat{\boldsymbol{\theta}}$ 를 이용하여 모델의 예측을 그래프로 나타냈다.

X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)),X_new]
y_predict = X_new_b.dot(theta_hat)
y_predict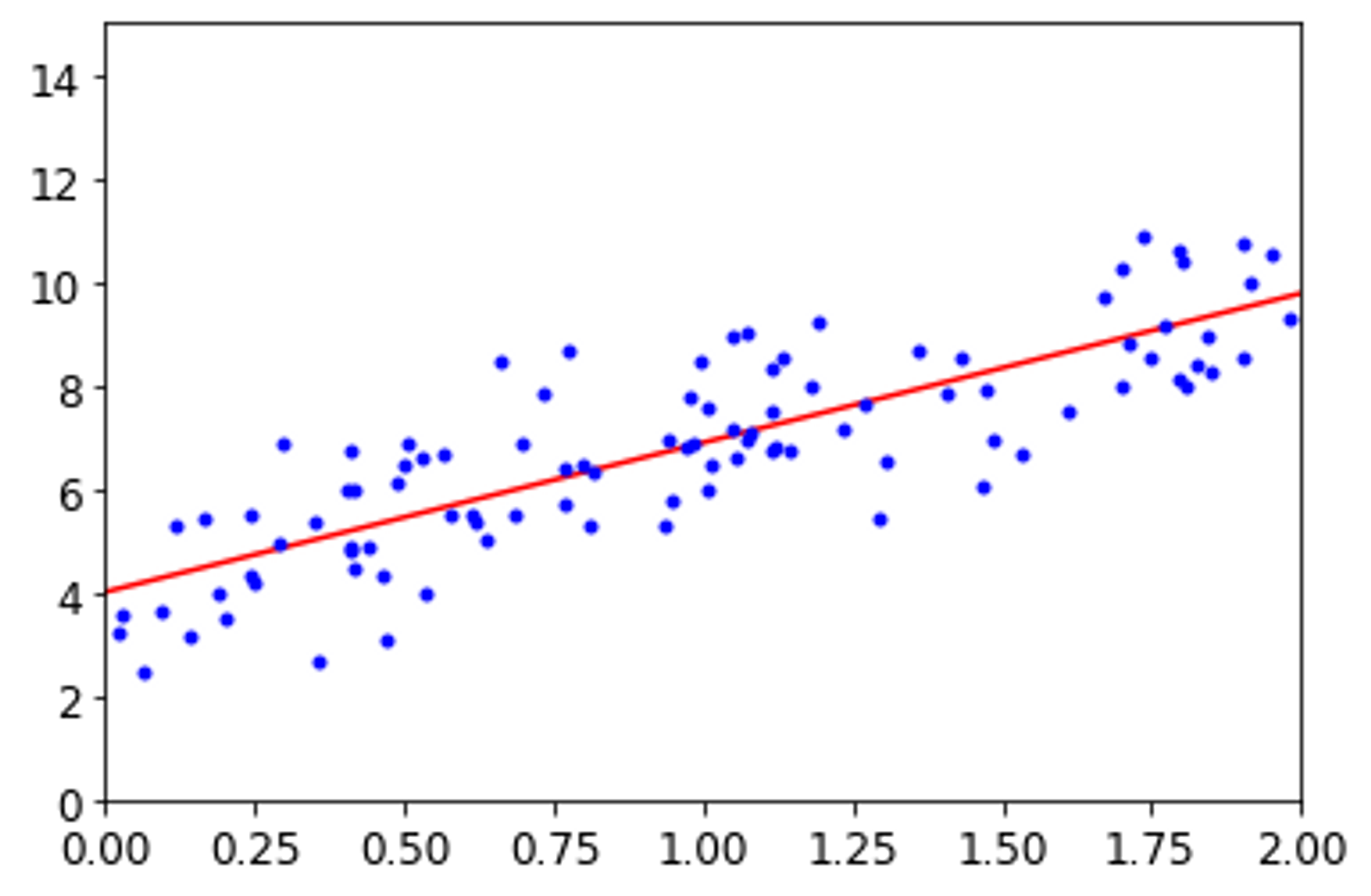

🟠 사이킷런을 통한 단순 선형 회귀

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)

lin_reg.intercept_,lin_reg.coef_

(array([4.01026541]), array([[2.88377652]]))

lin_reg.predict(X_new)

array([[4.01026541],
[9.77781846]])

array([4.01026541],[9.77781846]])

🟠 다중 선형 회귀

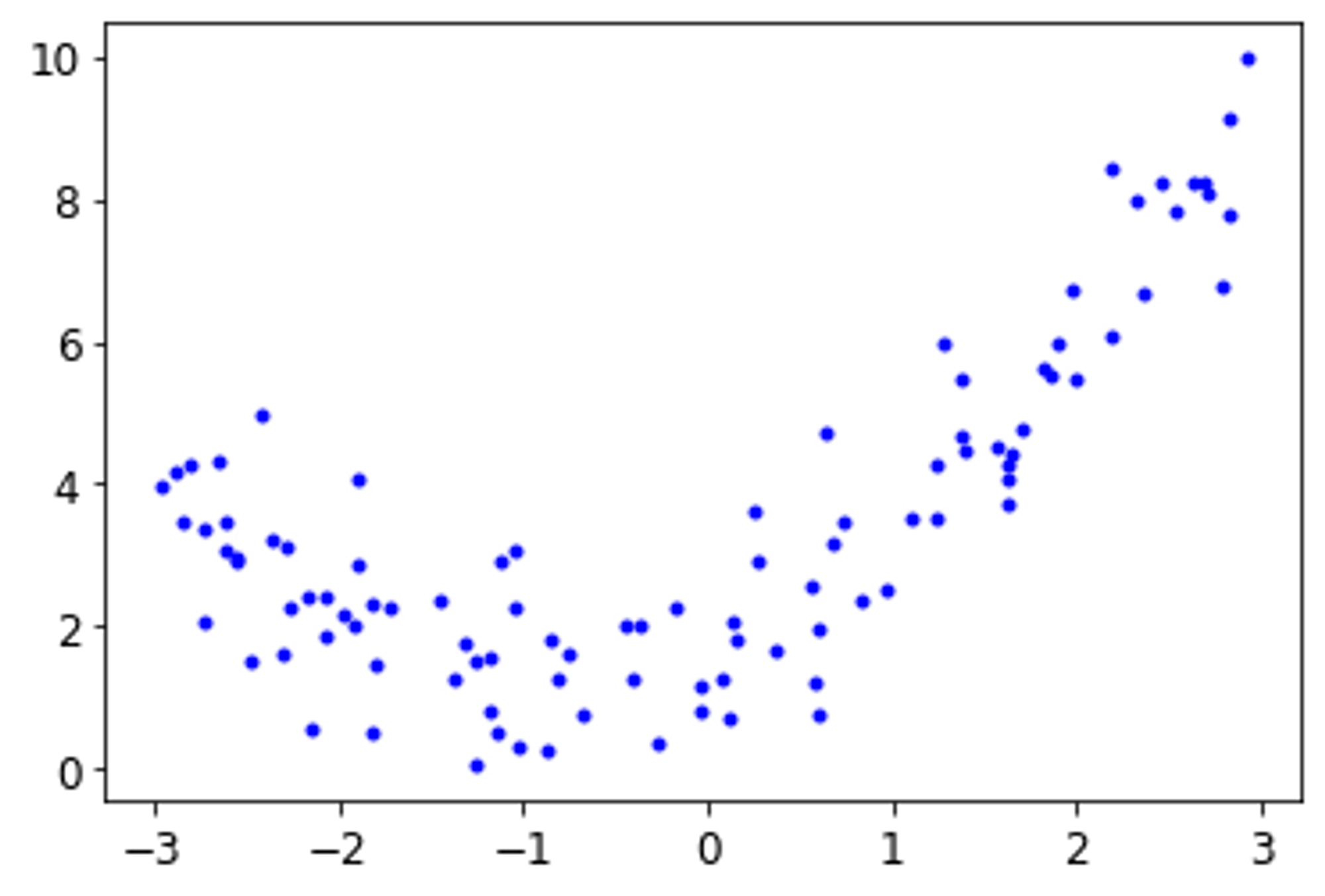
→ 2차 방정식으로 비선형 데이터를 생성 하였다.

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree = 2, include_bias = False)
X_poly = poly_features.fit_transform(X)

lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)
lin_reg.intercept_, lin_reg.coef_

(array([1.78134581]), array([[0.93366893, 0.56456263]]))

→ 다중 선형 회귀 분석을 위해 sklearn의 PolynomialFeatures 을 사용하였다. 훈련 데이터의 각 특성을 제곱하여 새로운 특성으로 추가한다. 이렇게 확장된 데이터를 LinearRegression 에 적용한다.

PolynomialFeatures(degree = d) 주어진 차수까지 특성간의 모든 교차항을 추가한다

따라서 특성이 여러 개일 때 다항회귀는 이 특성 사이의 관계를 찾는다.

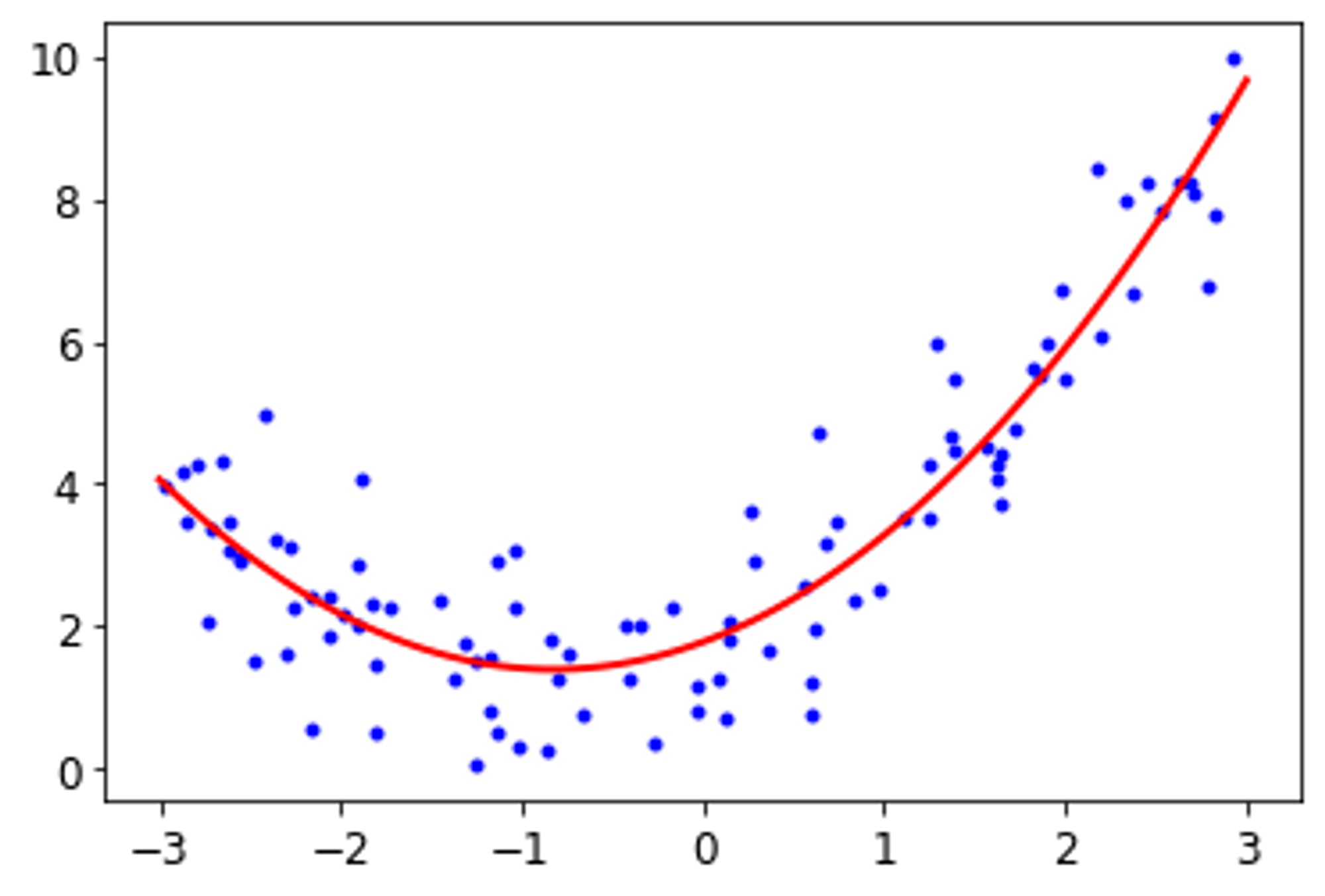
→ sklearn의 PolynomialFeatures를 이용하여 계수를 구했을 때 , 시각화로 나타내면 위의 그림과 같다 .

참조

핸즈온머신러닝
[Python] 선형회귀분석을 이론, 결과해석, 그리고 코드까지 (Linear Regression Model)

민정

공부 기록장

이전 포스트

[머신러닝] GBM (Gradient Boosting Machine) - 그라디언트 부스팅

다음 포스트