Orthogonality
두 vector 직교(Orthogonal)이면 수직이고 두 vector사이의 각도가 90도 임을 의미한다. 직교를 찾는 이유는 다음과 같다.
- Linearly independent basis
- Easy calculation in linear combination
Orthgonal vector는 basis vector이고 span이 가능하다는 이유도 있다.
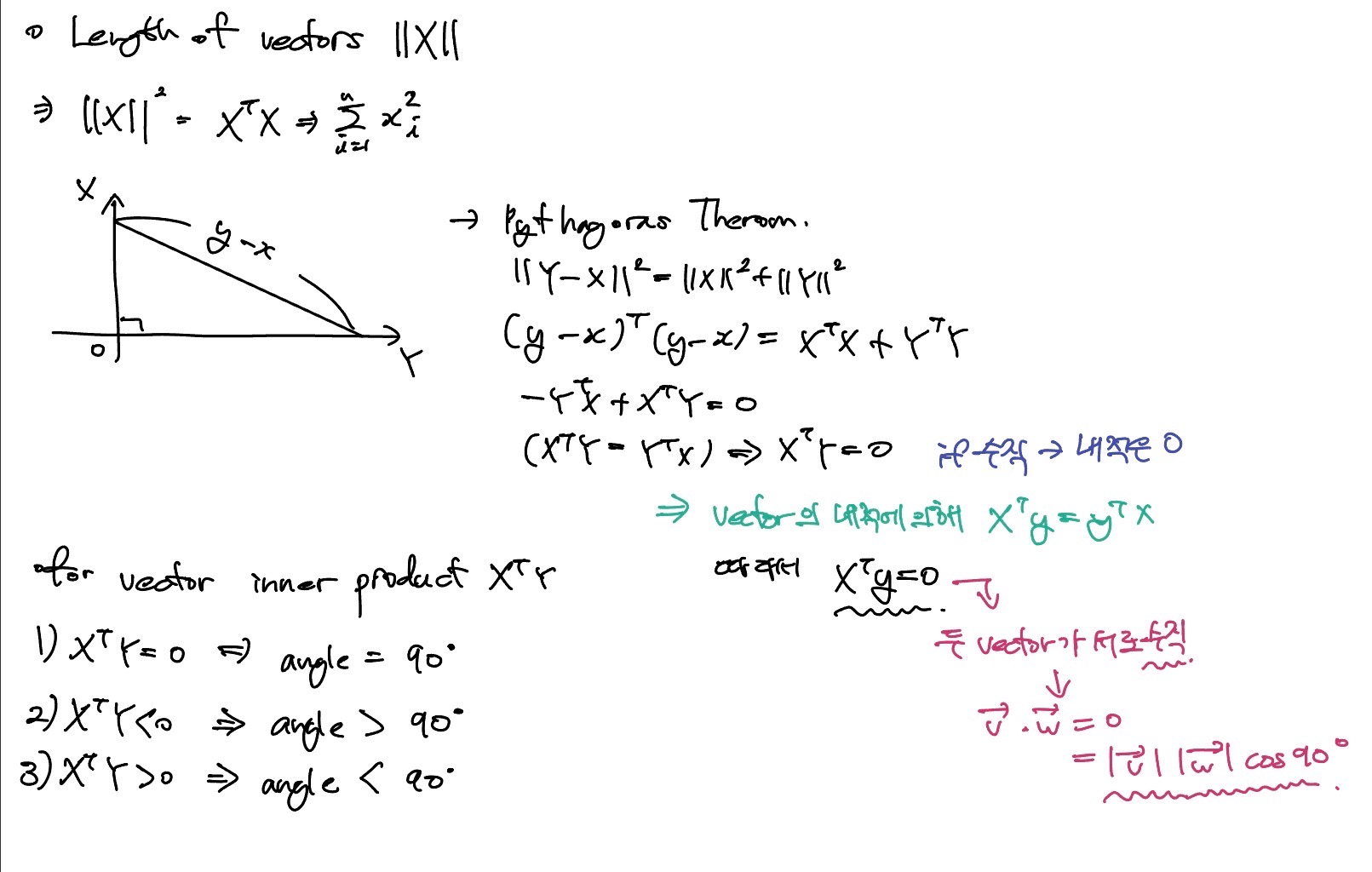
두 vector는 cosine에 의해서 직교할 경우 그 값이 0이된다.

Linear Independent는 다음의 수식일 때 의미한다.
모든 계수가 0이면 linear independent하다는것을 알 수 있다.
Orthogonal Subspaces
한 space에서 임의의 vector와 다른 space의 임의의 vector가 항상 직교한다는것은 두 space가 직교하는것을 의미한다.
두 subspace가 직교하기 위해서는 다음과 같이 두 조건이 필요하다.
- 한 subspace에 존재하는 모든 vector가 다른 subspace에 존재하는 모든 vector와 직교
- 두 subspace가 만나는 점은 오직 원점
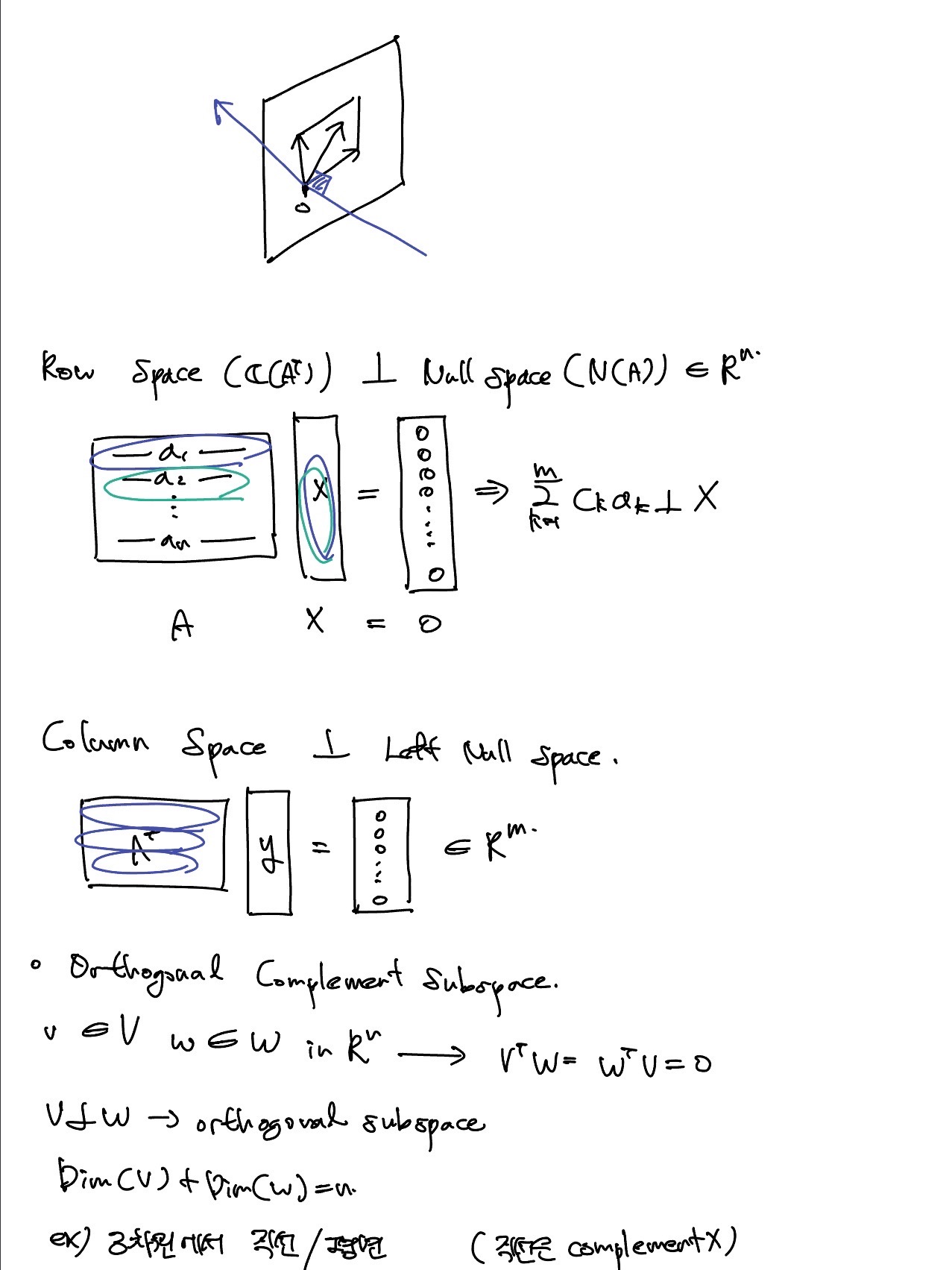
모든 subspace들의 수직은 행렬 A가 mxn일 때,
모든 space의 dimension은 다르다. 이때 dimension은 vector space를 이루는 linear independent한 vector의 개수를 나타낸다.
Dimension of Vector Space = Independent vectors to span the vector space = Rank of A(r)
Vector 와 가 수직이라면 orthogonal subspace라고 한다. 여기에 Dim(v)+Dim(w)= n이라는 성질이 추가되면 Orthogonal Complement Subspace가 된다.
예를 들어, 3차원에서 row space가 평면이면 대응되는 null space는 원점을 지나는 직선이고 평면과 수직이 된다. 따라서 3차원 공간 상의 직선과 수직인 선이 있다면 fundamental subspace에서 서로 보완관계를 가질 수 없다.
Orthogonal Complement Subspace
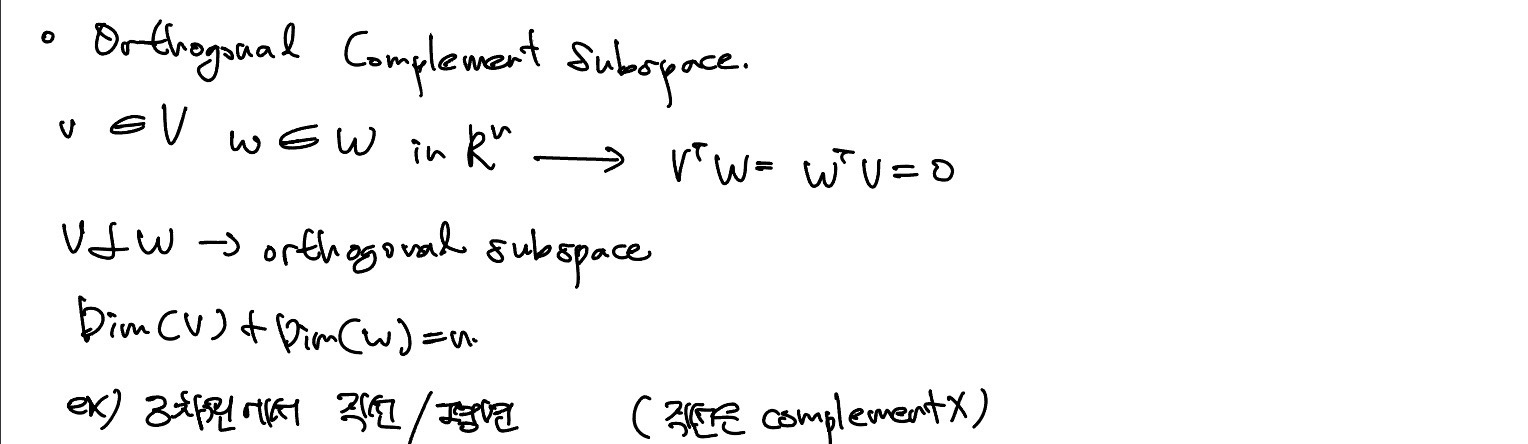
Cosines and Projection onto line
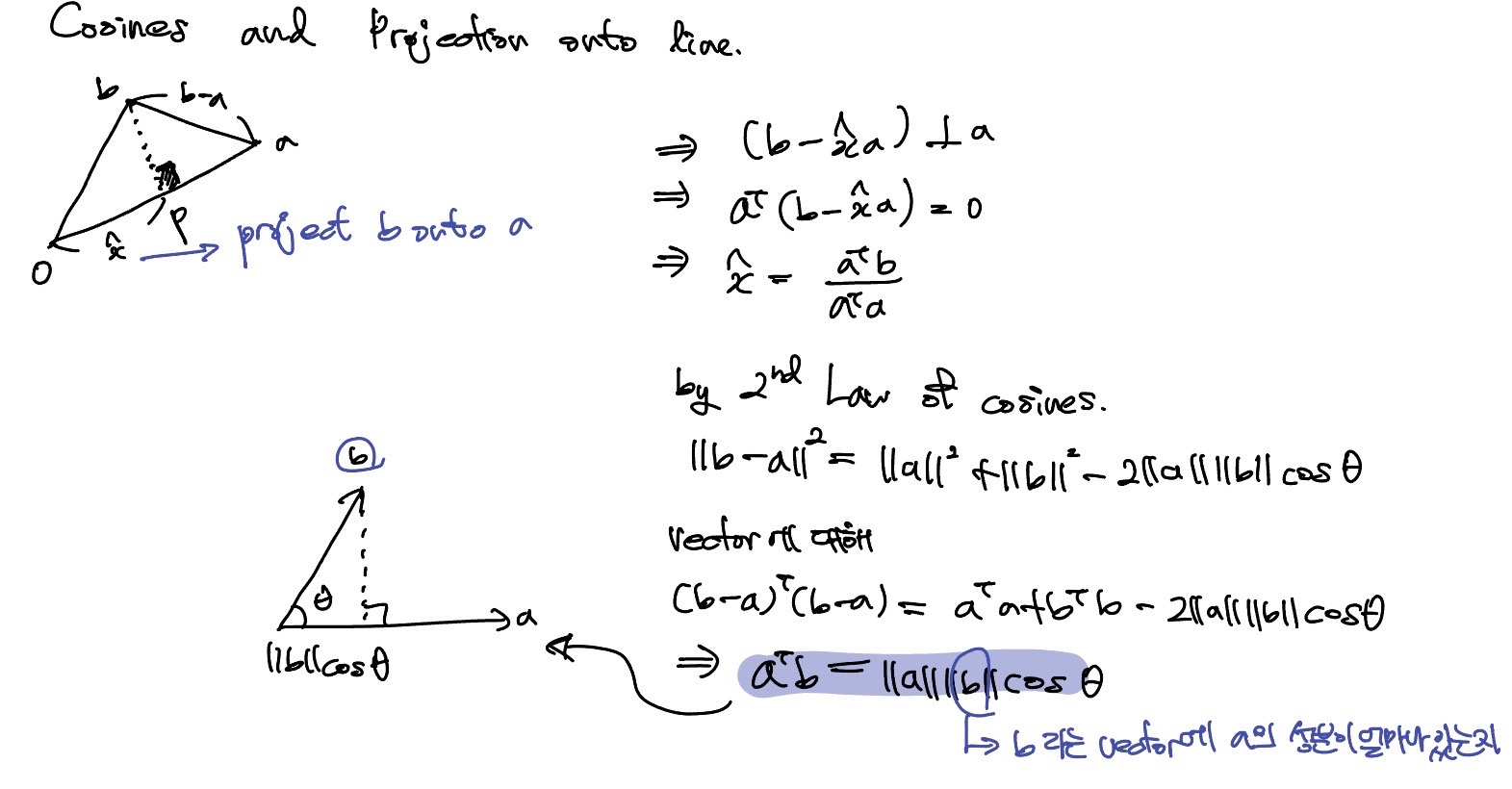
수선의 발을 내렸을 때, 좌표를 구하는, 가장 길이가 짧도록 투영하는것이다.

Projection Matrix에 투영하고자 하는 vector b를 곱하면 투영된 좌표 p가 나온다.
또한 공간상의 한점을 평면에 투영해서 얻은 수선의 발은 투영할 때 바뀌지 않는다.
