Review
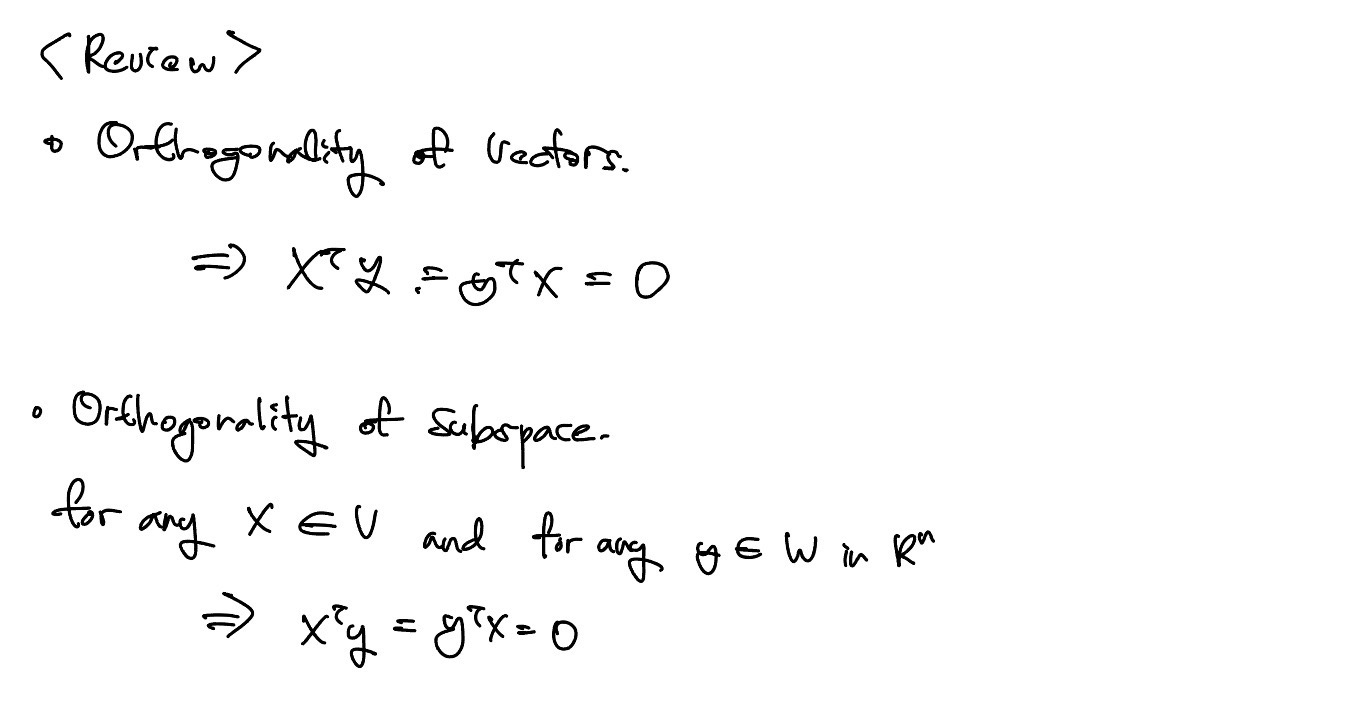
Vector space V,W가 n차원 space의 vector일 때, 모든 X, Y의 vector는 수직 관계이다.
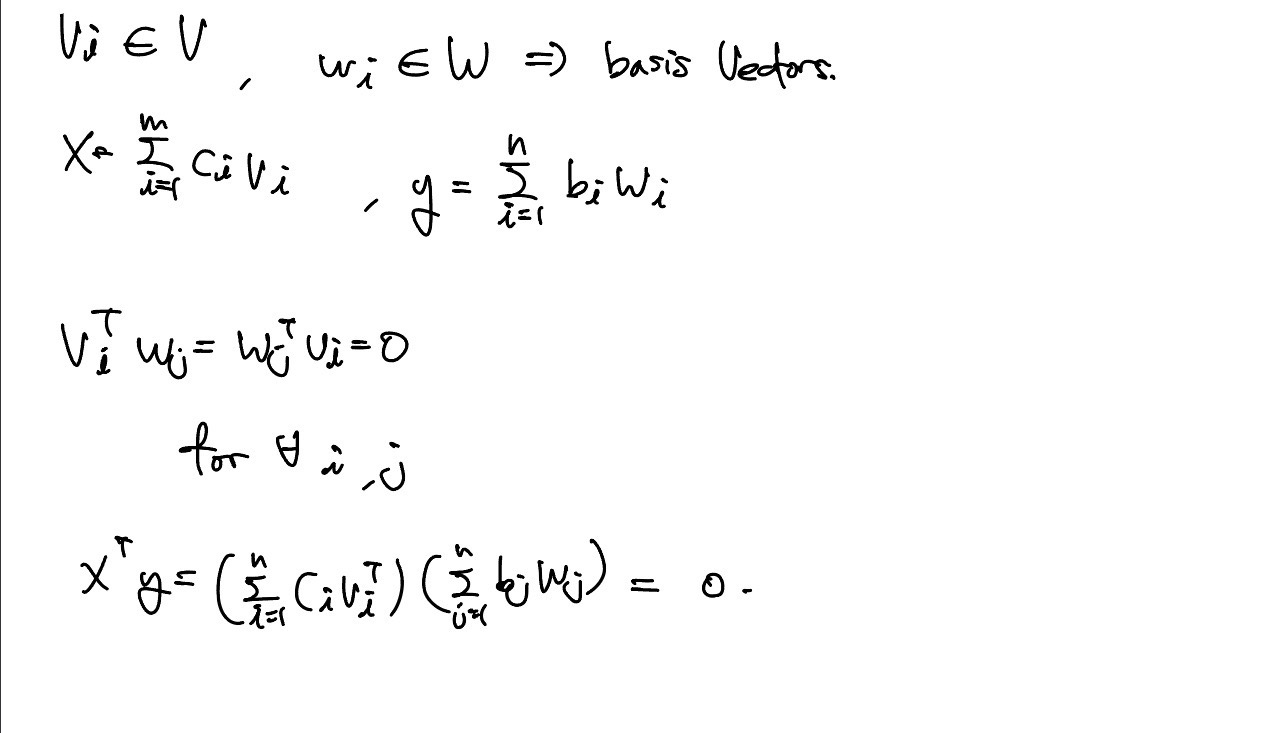
모든 vector가 수직관계라면 내적 값은 모두 0이다. 또한 vector space도 전부 수직이다. Linear independent한 basis vector들이 다른 vector와 수직관계라면 vector space의 수직관계를 알 수 있다. Basis vector는 space상에 대응점을 구한 뒤 independent인지 알 수 있다.
Vector가 모두 수직 = Vector가 Linear Independent
Projection onto line

Projection P라는 vector는 직선 a에서의 좌표에서 b와 가장 가까운점을 구하는것이다.
Projection and Least Squares
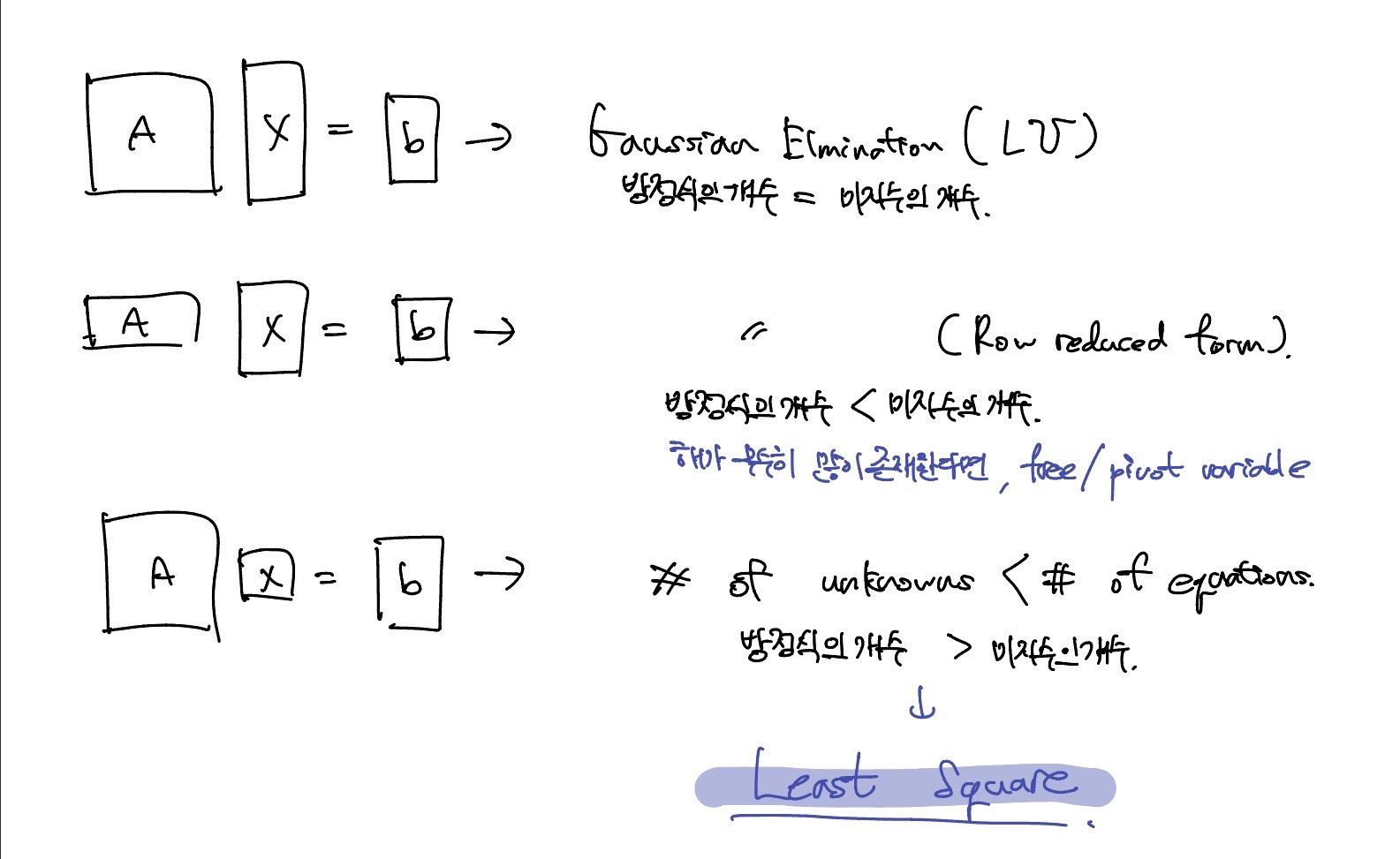
미지수의 개수보다 방정식의 개수가 많을 때는 최소제곱법, least squares를 사용한다
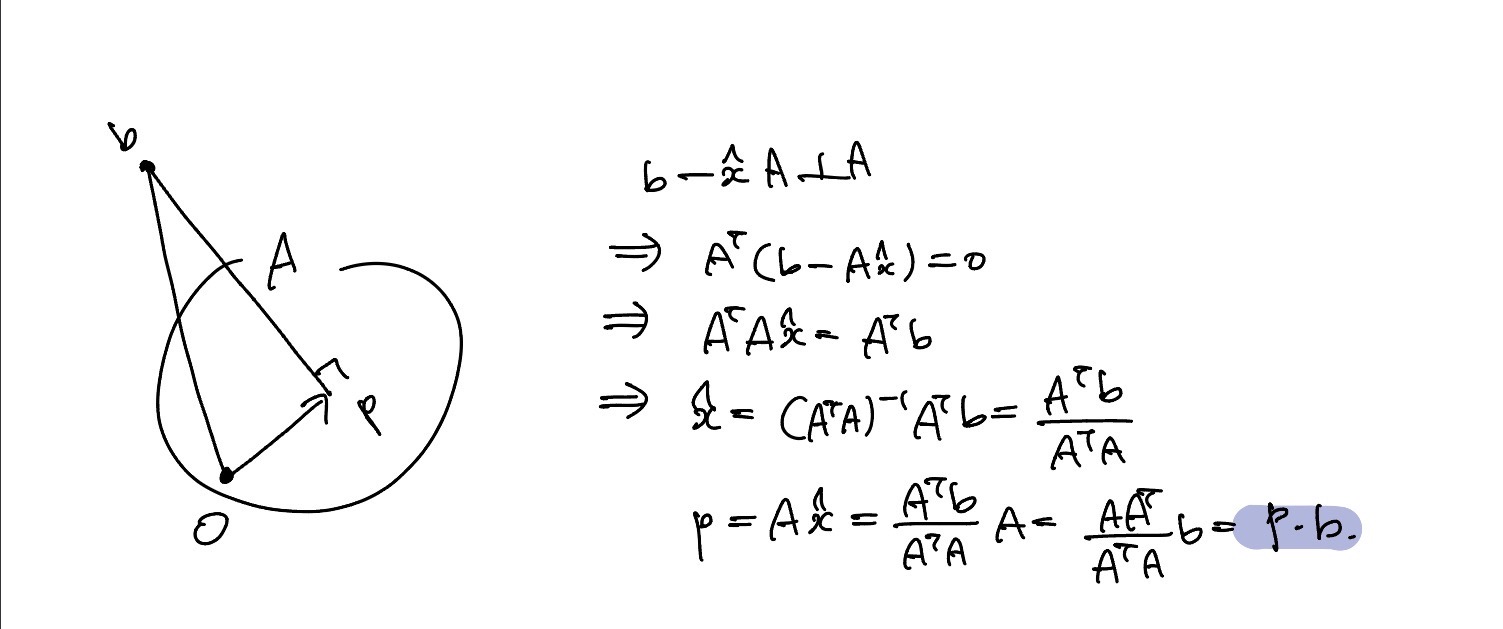
A는 column vector로 이루어진 column space이다. 위 그림을 통해, P라는 좌표에 해당하는 vector가 b라는 vector를 행렬 A로 이루어진 column space에 수직 방향으로 projection하면 최소거리가 된다.
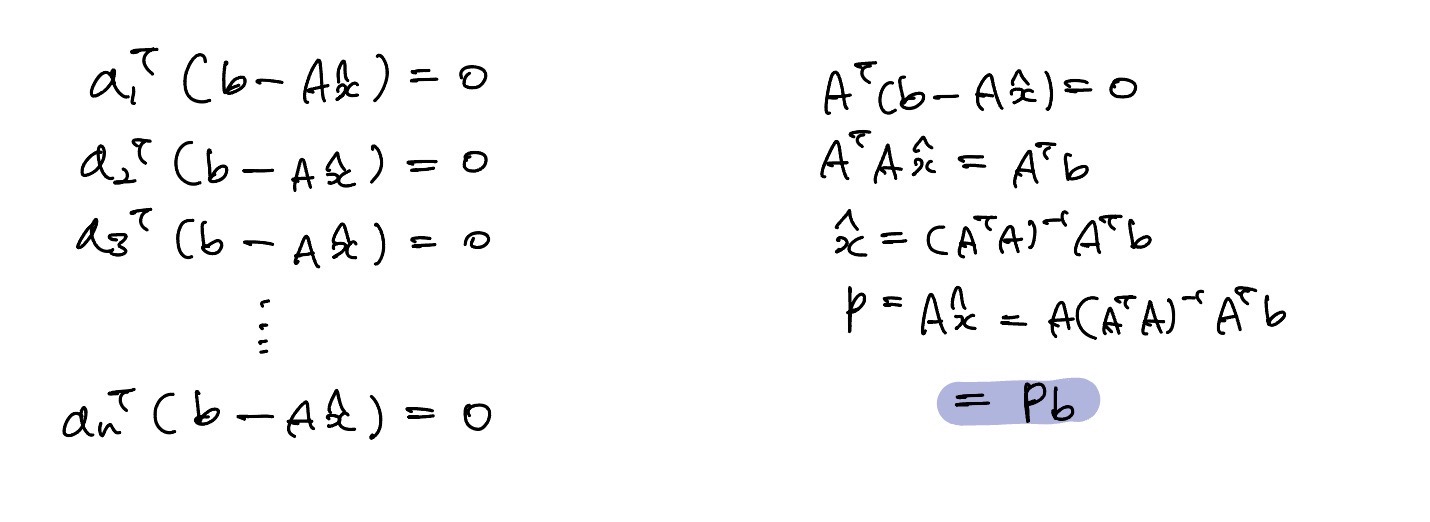
의 역행렬이 존재한다는 전제 하에 계산이 가능하다.
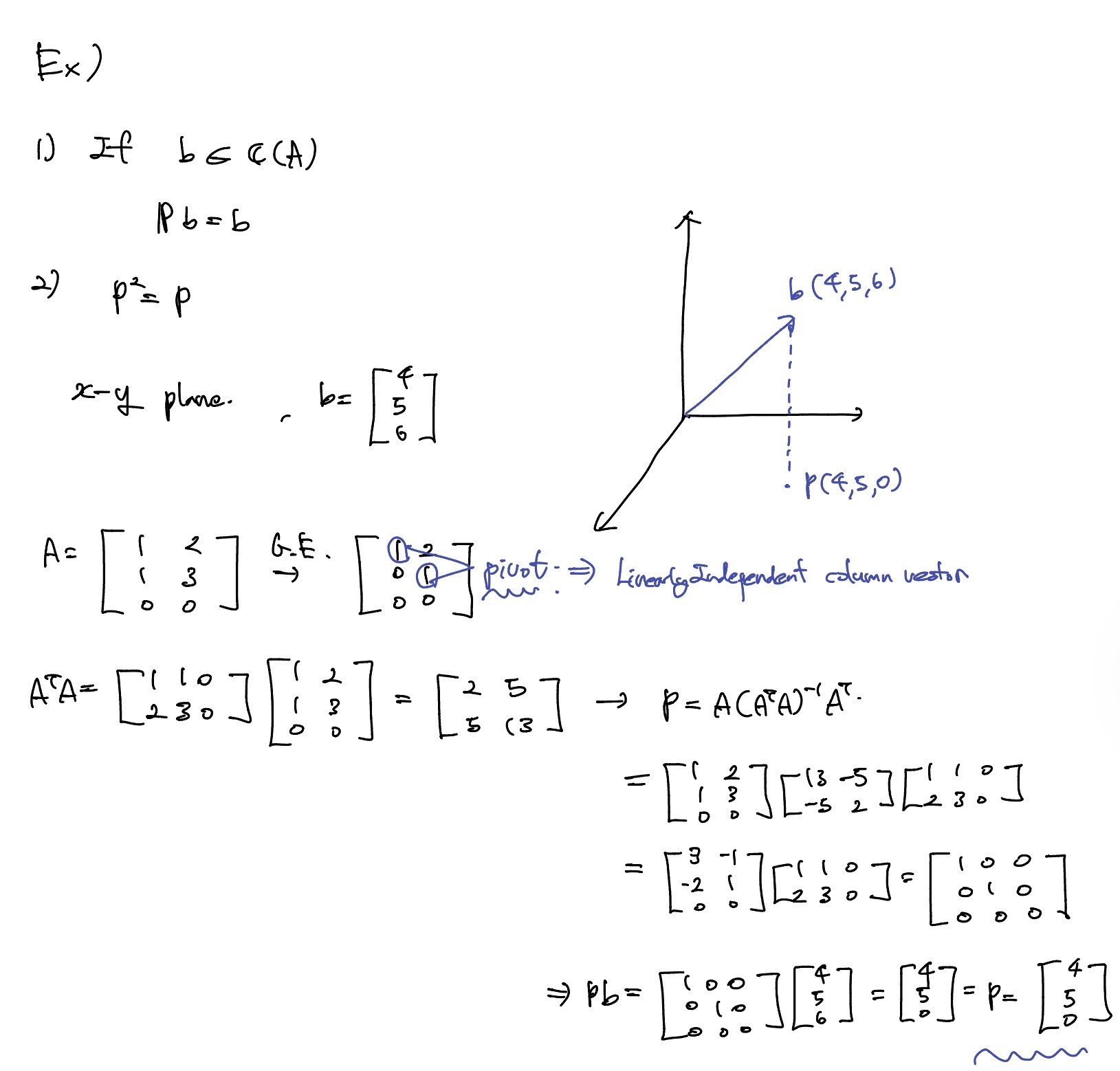
행렬 A는 x-y 평면으로 vector space를 표현하고 평면을 나타낼 수 있는 linearly independent한 column vector 2개를 가우스 소거법으로 matrix A를 찾아야한다. 이 행렬을 이용해 projection vector 와 좌표를 구할 수 있다.
Least square for line fitting
평면 상에 sample 좌표가 존재할 때, 하나의 직선으로 근사화한다.
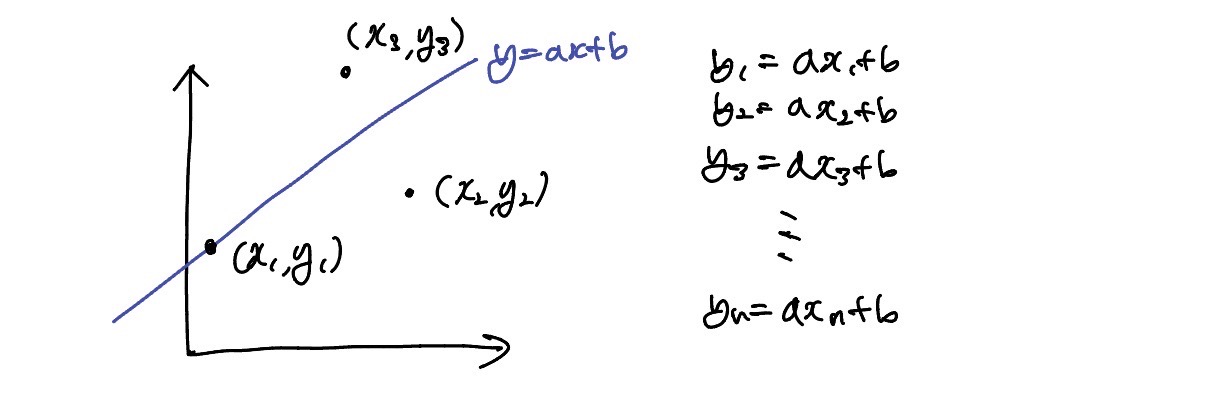
한 vector space에 data가 주어졌을 때, 이 모든 data를 하나의 직선으로 근사화하려고 한다면 직선이기 때문에 기울기와 절편만 필요하다.
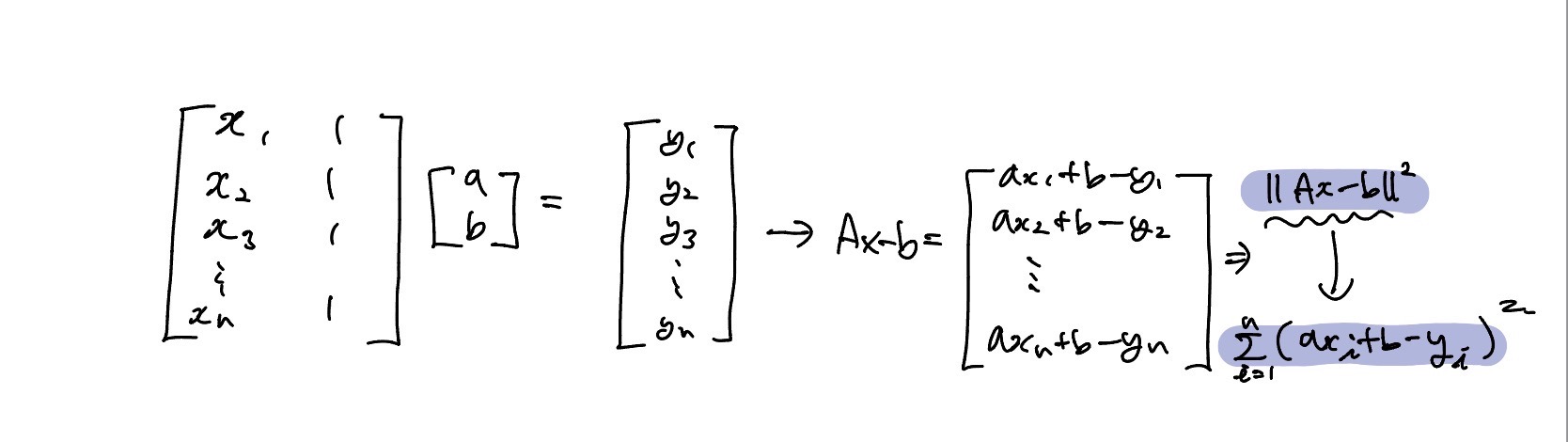
직선을 행렬로 표현할 수 있고 least-square 형태의 Ax=b 형태로 표현할 수 있다. 미지수의 개수보다 식이 더 많을 때 Least Square가 필요하다.
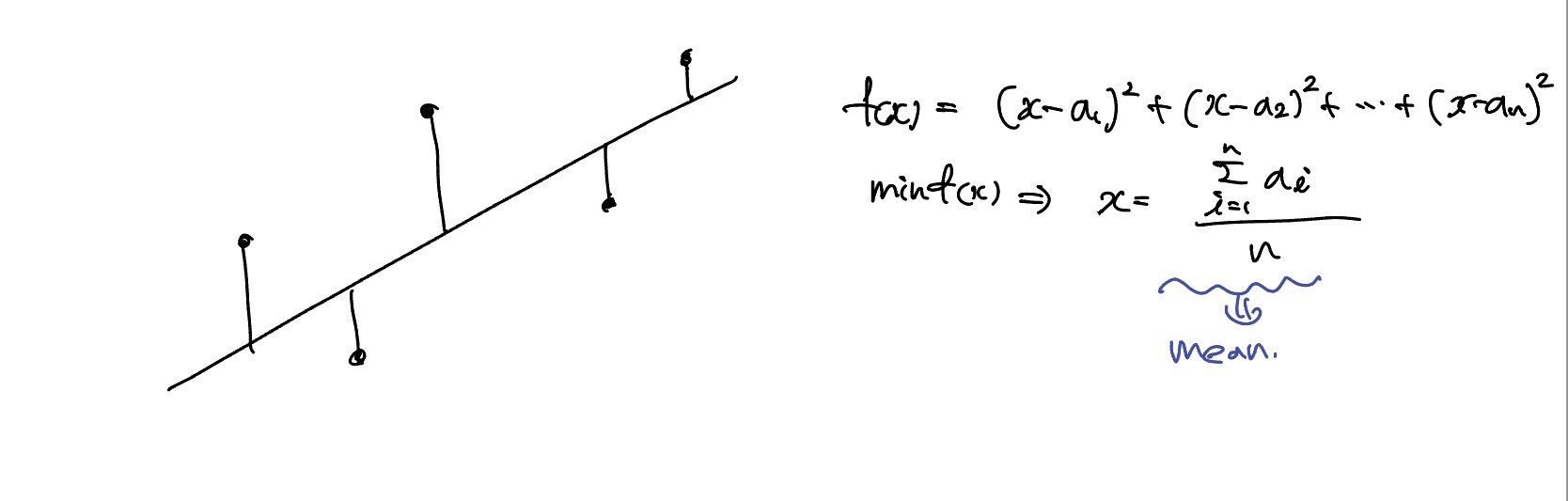
위의 직선이랑 점 사이의 distance가 가장 짧을 수 있는 직선을 구해야한다. 거리의 제곱합으로 이루어져 있는 함수 가 있을 때, 이 함수를 최소화하는 x는 a의 평균이다. Least Square로 해를 구하면 최소한의 개수로 구할 수 있는 해의 평균값으로 볼 수 있다.
Cost Function
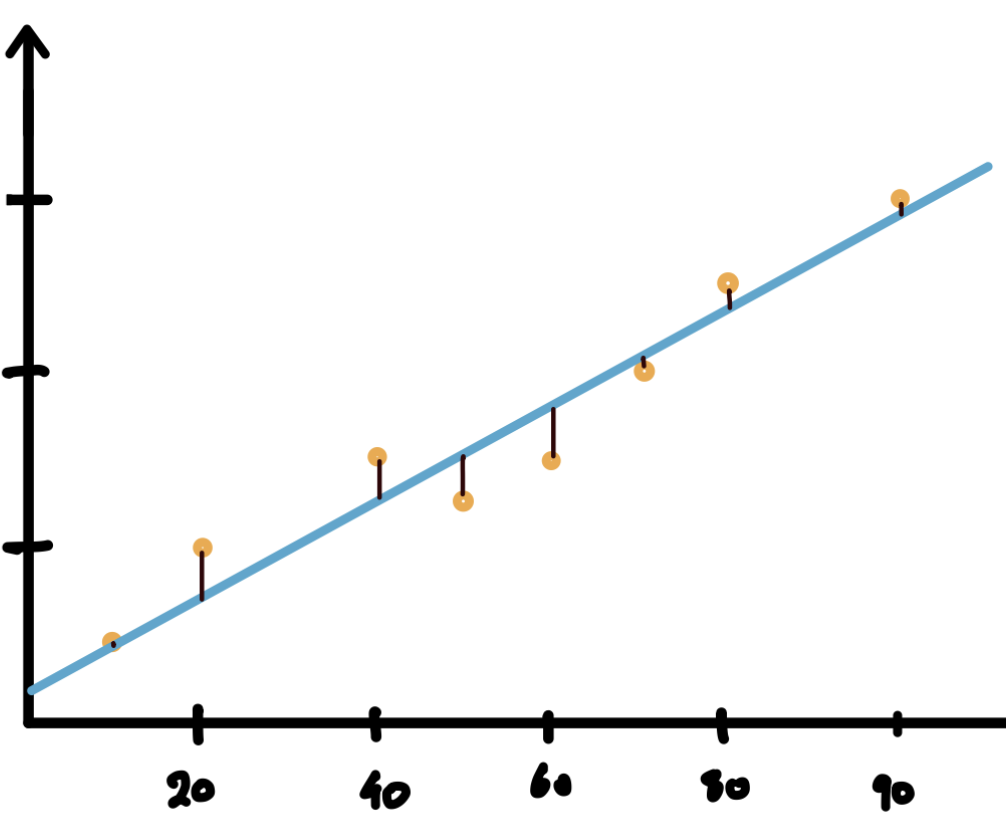
이번 강의에서 배우는 least square는 결국 머신러닝의 cost function과 연관되는것을 알 수 있었다.
머신러닝의 regression는 결국 두 변수 x,y의 선형관계를 하나의 선으로 나타내는것이다. 이때 어떻게 선을 그어야 가장 잘그은것일까?
이때 사용하는것이 바로 cost function이다. 점과 직선사이의 거리를 구하는 방법은 다음과 같다.
Least square가 거리의 제곱합의 평균을 이용한것을 보면 같은 개념으로 보여진다.