Linear Transformation
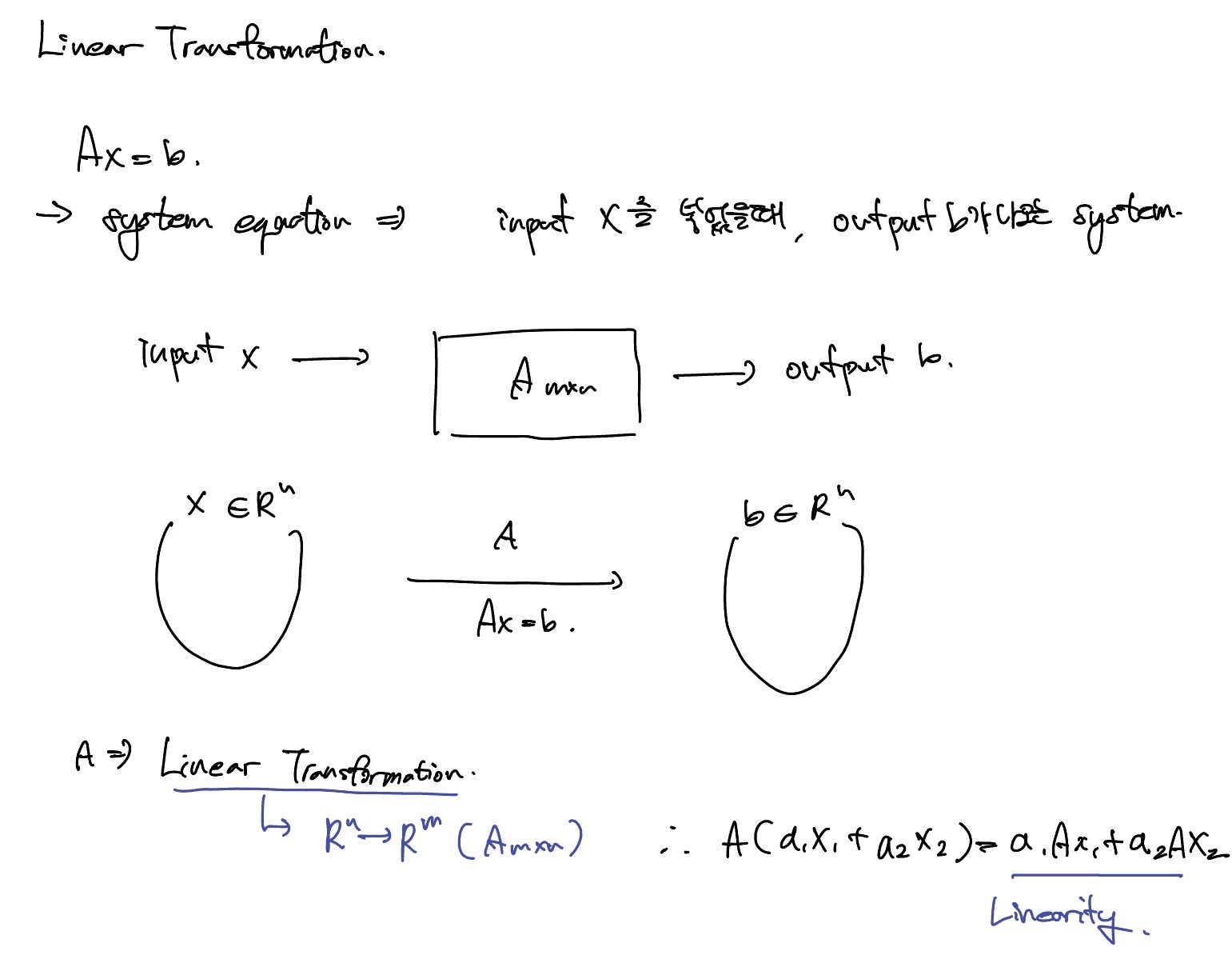
행렬 A를 하나의 system으로 본다면 X는 input vector, b는 output vector로 생각할 수 있다.
행렬 A의 dimension이 mxn일 때, Ax=b는 n차원 space의 vector X를 m차원 space의 vector b로 mapping하는것으로 볼 수 있다. 이때 A를 linear transformation vector라고 한다.
- is transformed/mapped into b by A
Example
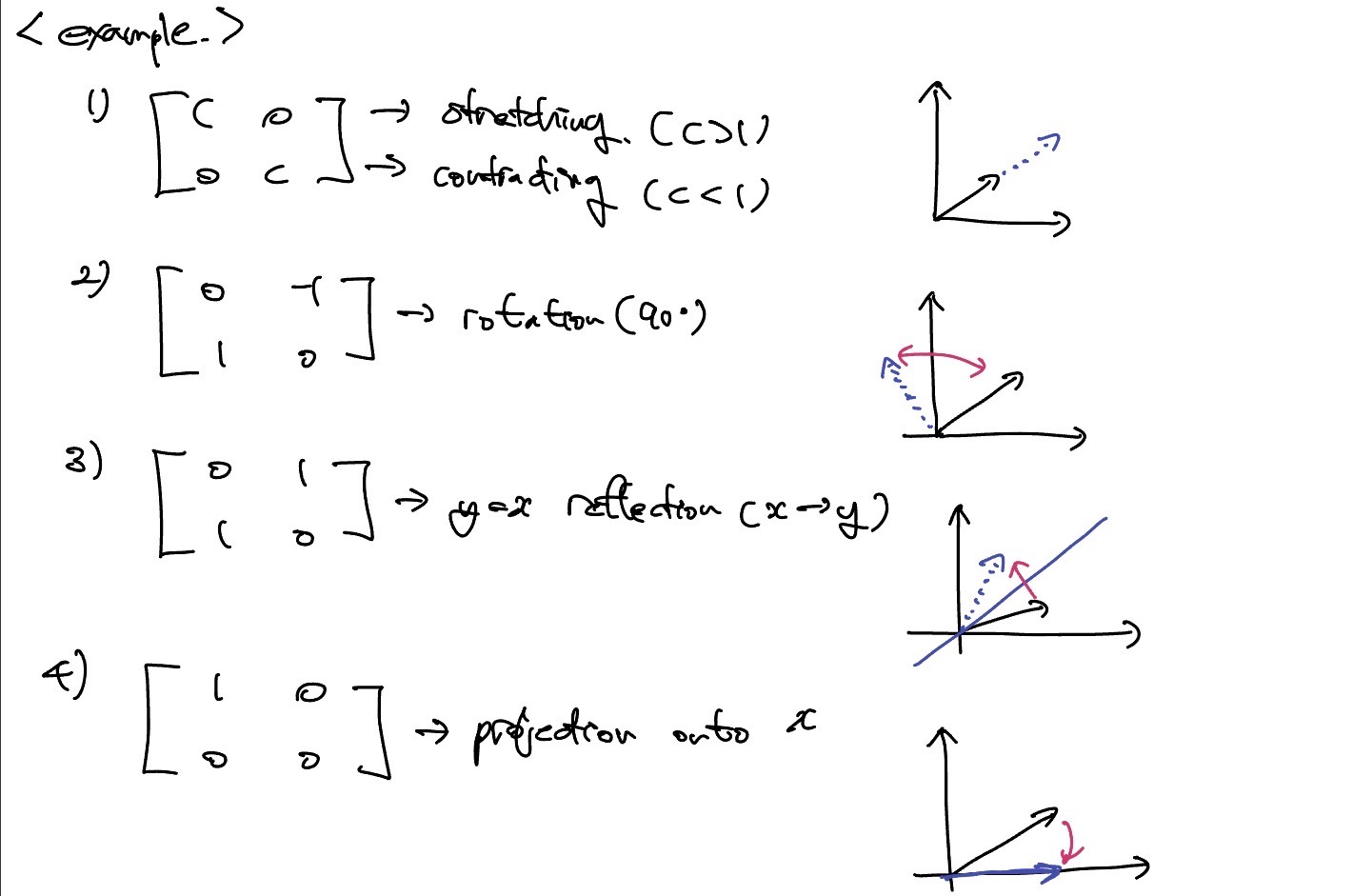
행렬은 linear transformation 과정으로 이해할 수 있고, 모든 linear transformation은 행렬로 표현할 수 있다.
Differentiation
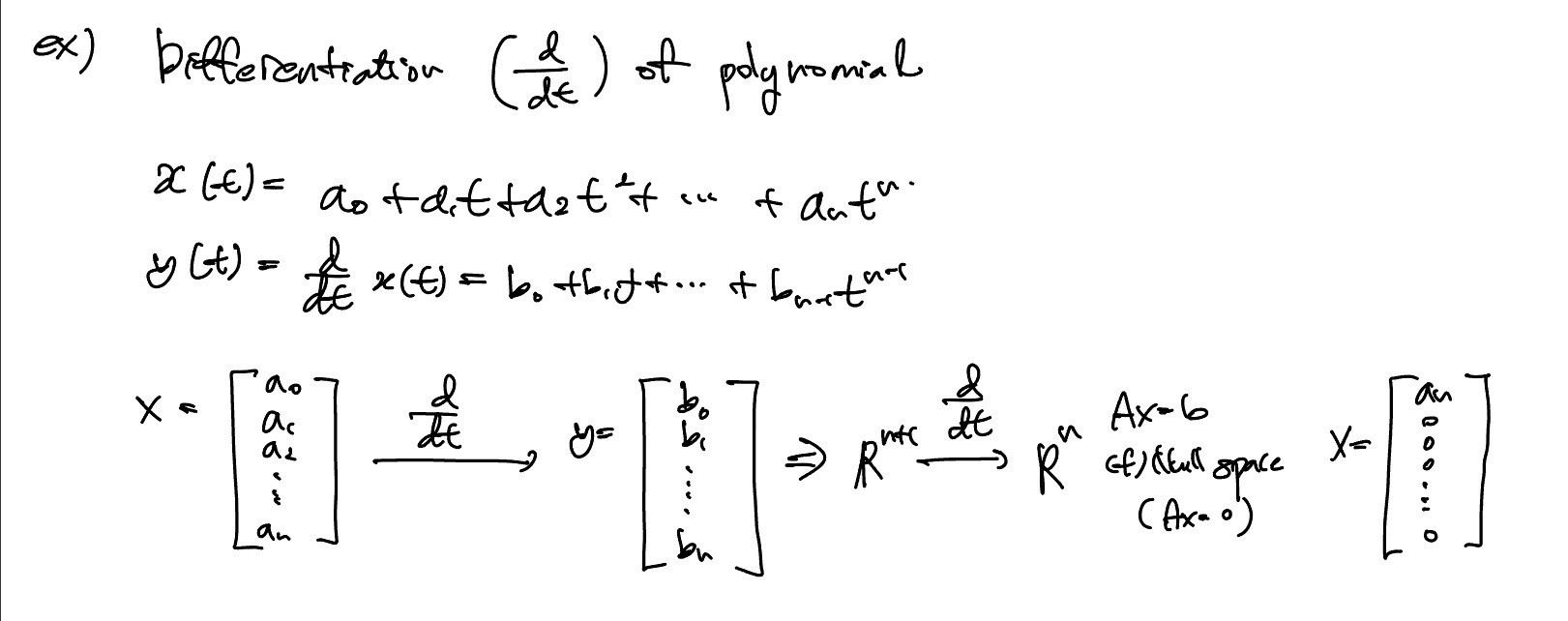
미분은 n+1 dimension에서 n dimension의 space로 transform하는것이니 linear transformation이라고 볼 수 있다.
Integration
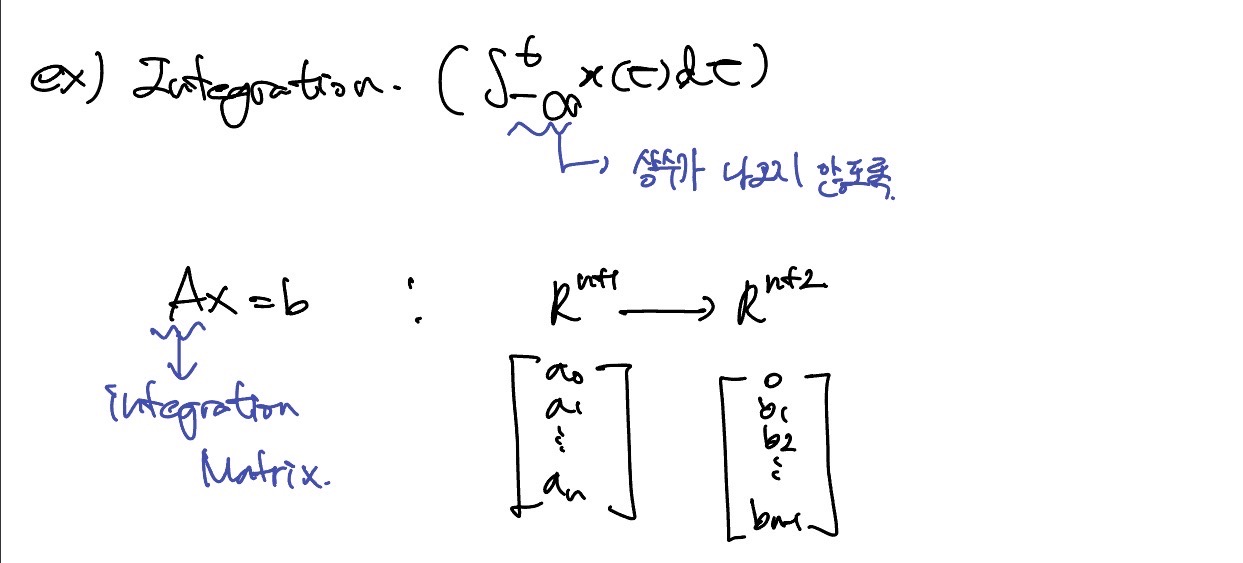
그렇다면 적분은 n+1 dimension에서 n+2 dimension으로 변한다.
Multiplication
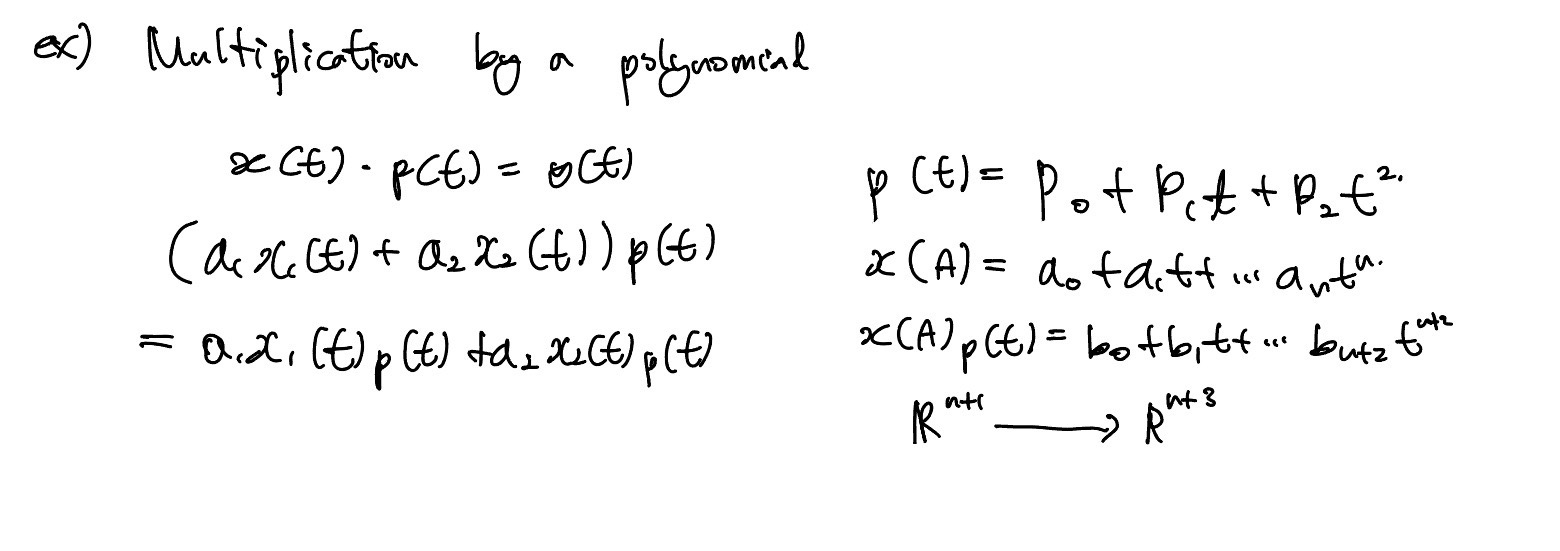
Linear Transformation이라 하는 행렬 A는 어떻게 구할까?
모든 Basis vector에 대해 Ax값을 알고 있으면 vector space 내의 모든 x에 대해 Ax값을 알 수 있다.
- vector space의 모든 x는 Basis에 의해 표현될 수 있기 때문에 A를 몰라도 Ax는 구할 수 있다.
즉, 어떠한 vector들도 basis vector의 linear combination이기 때문에 계수만 조합하면 tranform한 결과를 알 수 있다.
Find A
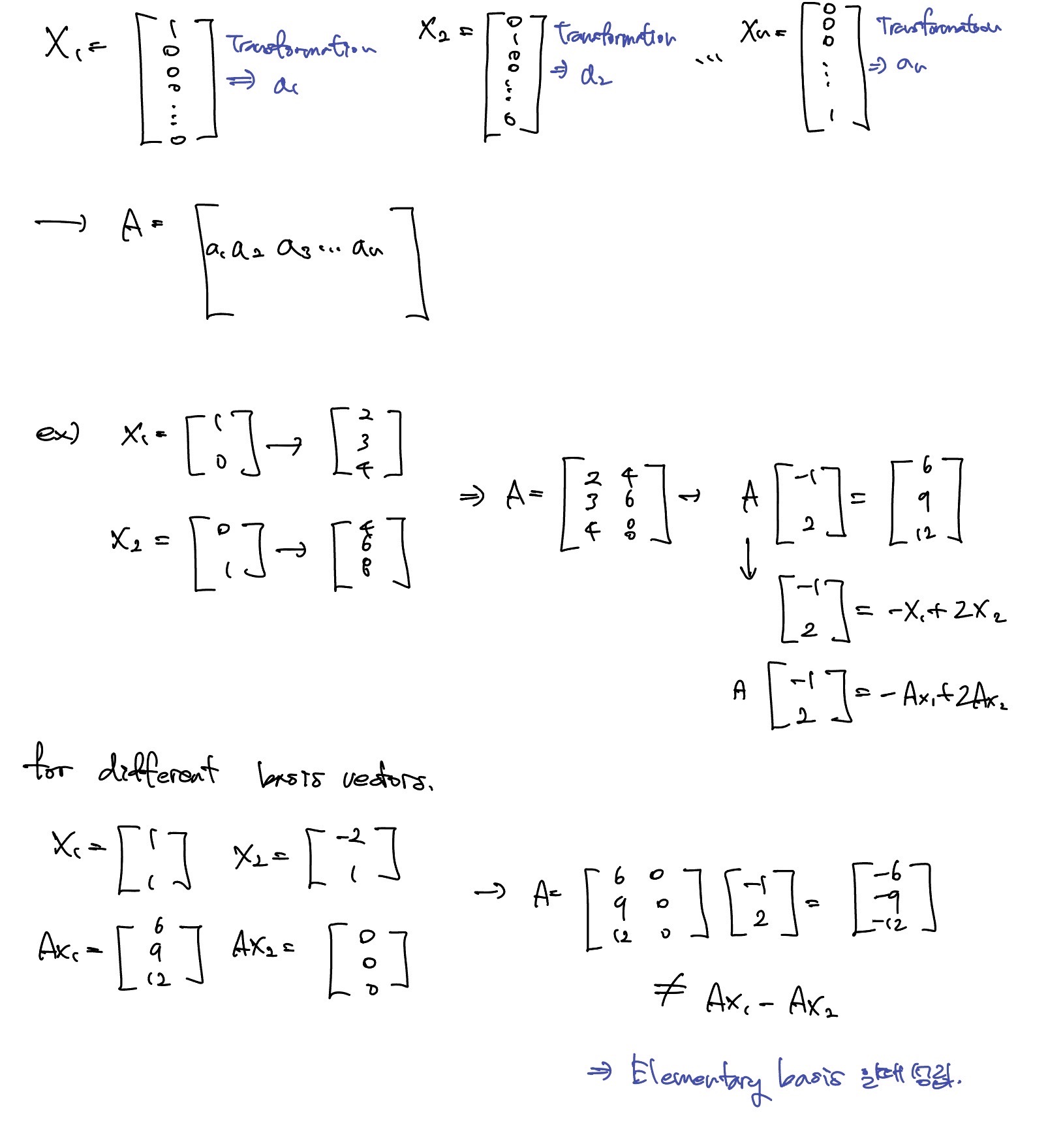
Elementary basis vector들의 Ax값을 안다면 A는 쉽게 구할 수 있다.
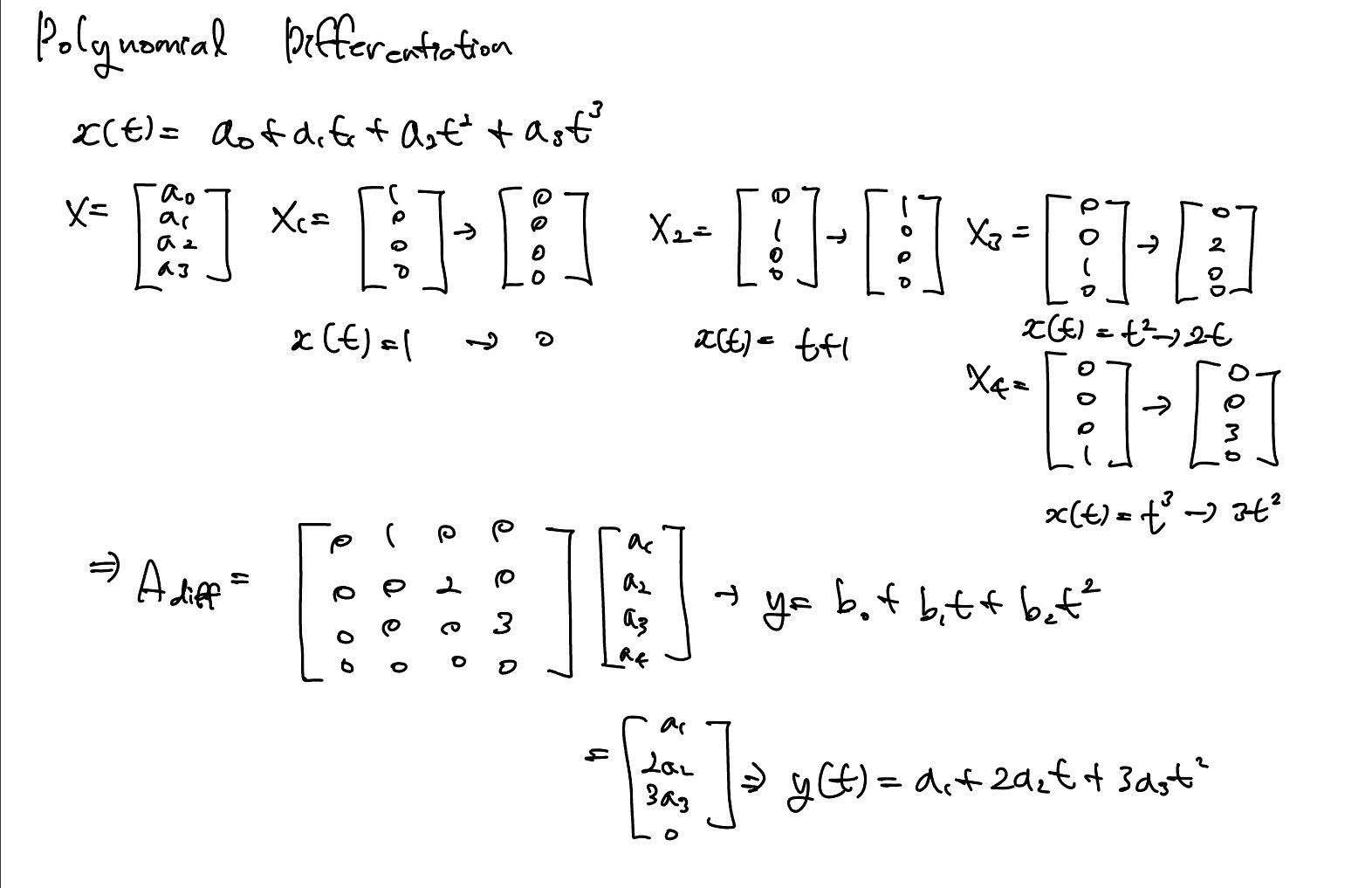
Polynomial Differentiation
미분도 linear transformation이므로 다항함수에 적용해 행렬A로 표현할 수 있다.
Polynomial Integration
적분도 마찬가지다.

만약 적분했다가 미분하면 다른 값이다.
- Differentiation is a left inverse of integration