이번 강의에서는 Linear Independce와 Basis에 대해서 배웠다. 먼저 선형독립과 기저벡터는 머신러닝에서 차원축소(PCA, SVD)와 LDA에서 들었던 기억이 있다.
Review


먼저 지난 강의에서는 rectangular matrix의 경우 null space와 null space가 아닌 Ax=b의 해집합을 어떻게 나타낼지에 대해 배웠다. 가우스 소거법을 통해 Row-Reduced form의 형태로 만들어준다. 그리고 free variable과 pivot variable을 구분해준다. 그리고 linear combination의 scala에는 free variable 끝에는 pivot variable 계수만 둔다. 마지막으로 null space에서 linear combination을 만든다.
Linear Independence

선형독립이란 임의의 scalar값을 vector앞에 곱했을 때의 값이 모두 더했을 때 0이 되는것이다. 이때 scala값이 0이여야한다. 그래서 가우스 소거법을 통해 나온 행렬의 형태에서 모든 column vector들은 선형 독립이다.
b3-2b2+5b1 = 0을 만족해야 해가 존재한다는것이 성립한다. 즉 Ax=b에서 b가 column space에 속해 있어야 한다.
Rank of A

A의 Rank는 column의 수와 동일하고 이는 pivot의 개수와 동일하다. 만약 종속이라면 Rank의 수는 column보다 작으며 free variable이 존재한다.
Span

Span이란 어떤 vector들의 선형결합 조합들이 하나의 vector space를 이룰때 그 vector들은 해당 vector space에 span한다고 한다.
2개의 column vector들은 선형결합이 2차원 평면으로 span할 때 unique하지만 3개의 column vector들은 2차원 평면으로 span할 때, 여러개의 선형조합이 존재한다.
Basis
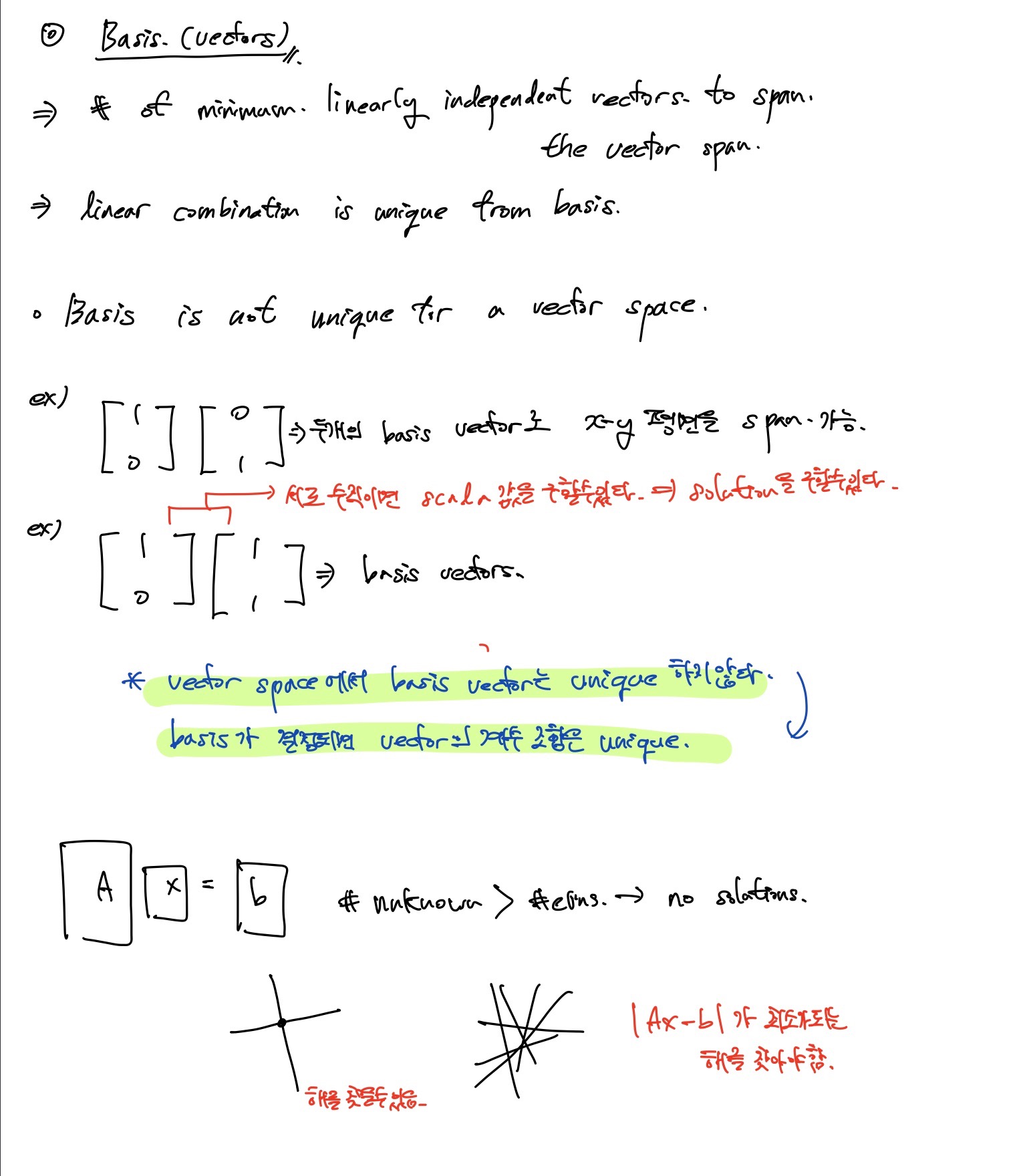
Basis(기저 벡터)란 vector space를 span하는 선형 결합 vector의 최소 개수이다. 그러므로 위의 예시에서 3개의 column vector일 경우 basis라고 할 수 없다.
그러나 basis는 vector space를 span하는데 있어 unique하지 않다. 2차원 평면를 span할 때 linear independent vector의 개수는 수없이 존재하기 때문이다. 그러나 특정한 basis안에서 vector의 선형결합의 scala값은 unique하다고 볼 수 있다. 또한 선형결합을 이루는 vector들이 서로 수직이면 연립방정식의 solution을 쉽게 구할 수 있다.