Review
Linear Independence
Linear Independence는 서로 다른 vector를 통해 다른 하나의 linear combination을 만들지 못하는 vector들의 조합을 의미한다.
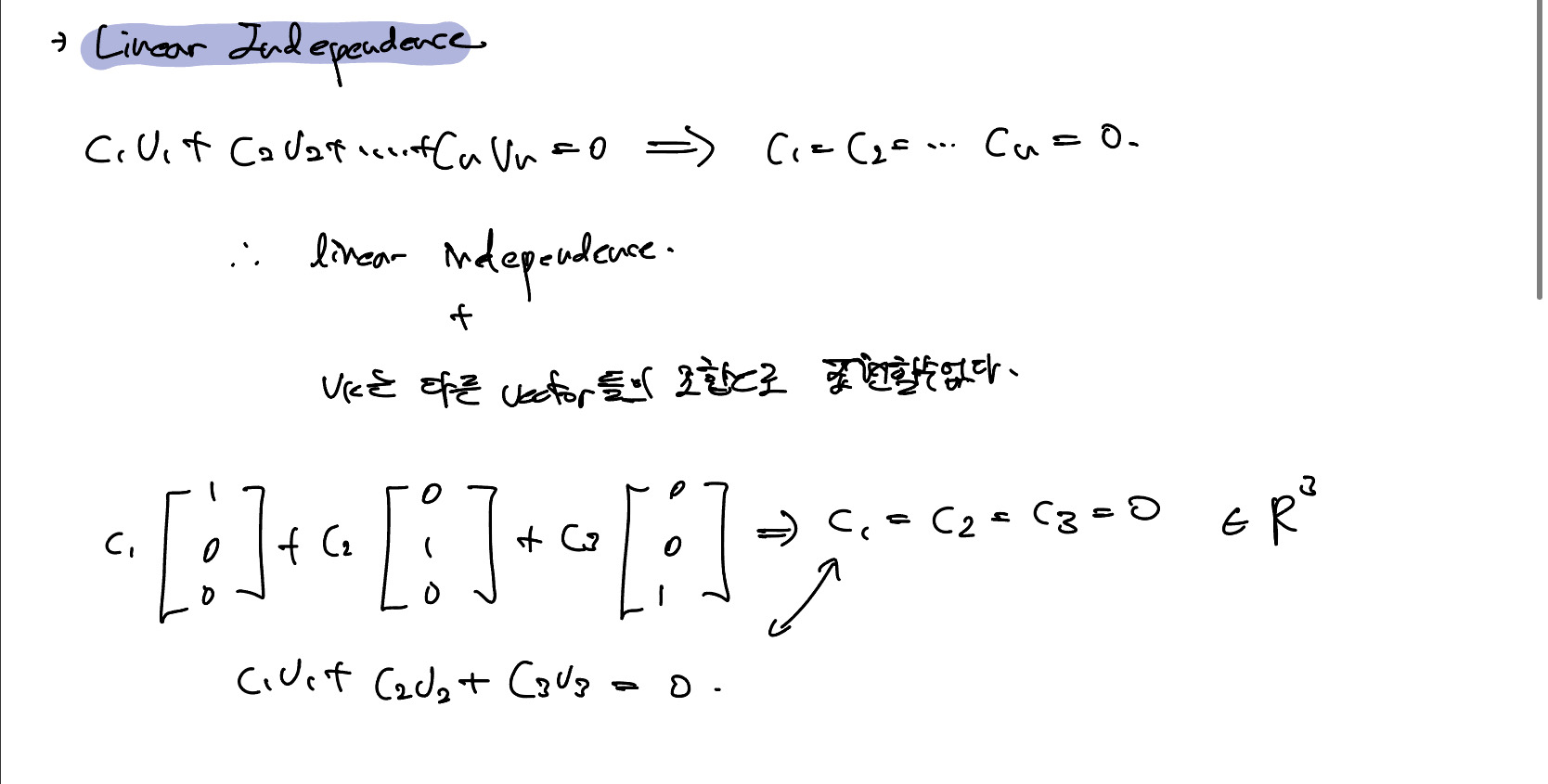
Spanning
Span이란 vector를 가지고 vector space를 만들 수 있는 모든 linear combination을 의미한다. 그리고 vector space를 span하는 vector의 집합은 unique 하지 않다.
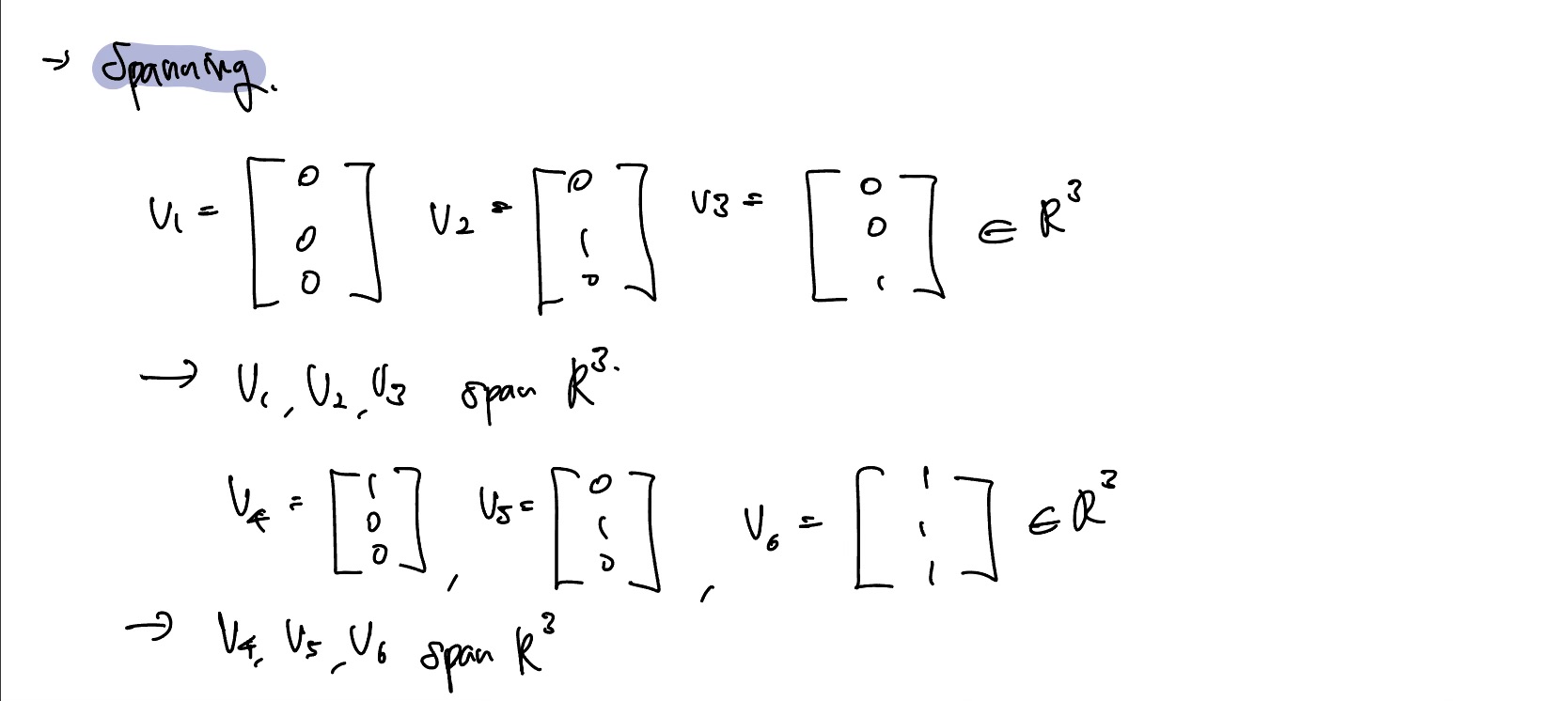
Basis
Basis란 vector space로 span하기 위한 최소한의 vector를 의미한다. 최소한의 수로 vector space를 span하기 위해서는 vector가 모두 independent 해야한다.
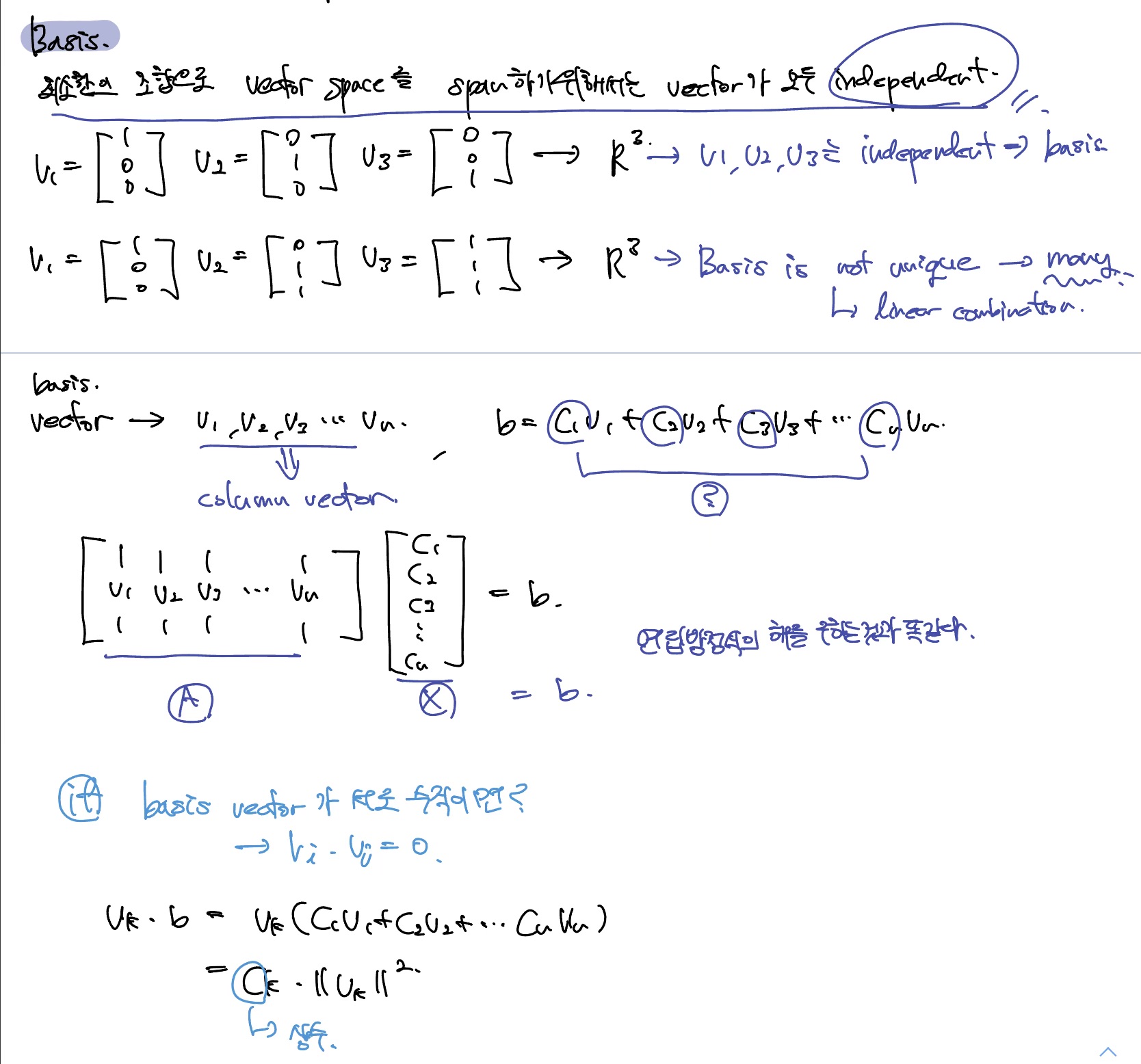
Basis는 기본적으로 linear independent을 이루는 최소의 unique한 vector의 집합이고 basis 자체는 unique하지 않고 여러개 존재한다. 그리고 가장 적절한 basis를 선택하기 위해서는 linear independence를 이루는 vector들끼리 서로 수직을 이루고 있는 basis를 고르면 된다.
Fundamental Subspace in A

먼저 Column space는 column vector로 이루어진 linear combination의 조합을 의미한다.
두 번째는 Null Space, 영벡터공간이다.
세 번째, Row space는 row vector로 이루어진 linear combination의 조합을 의미한다. Row space를 구하기 위해서는 행렬 A의 transpose한 후, column vector들의 linear combination을 구하면 된다.
마지막으로, 행렬 A의 transpose한 상태에서의 null space이다.
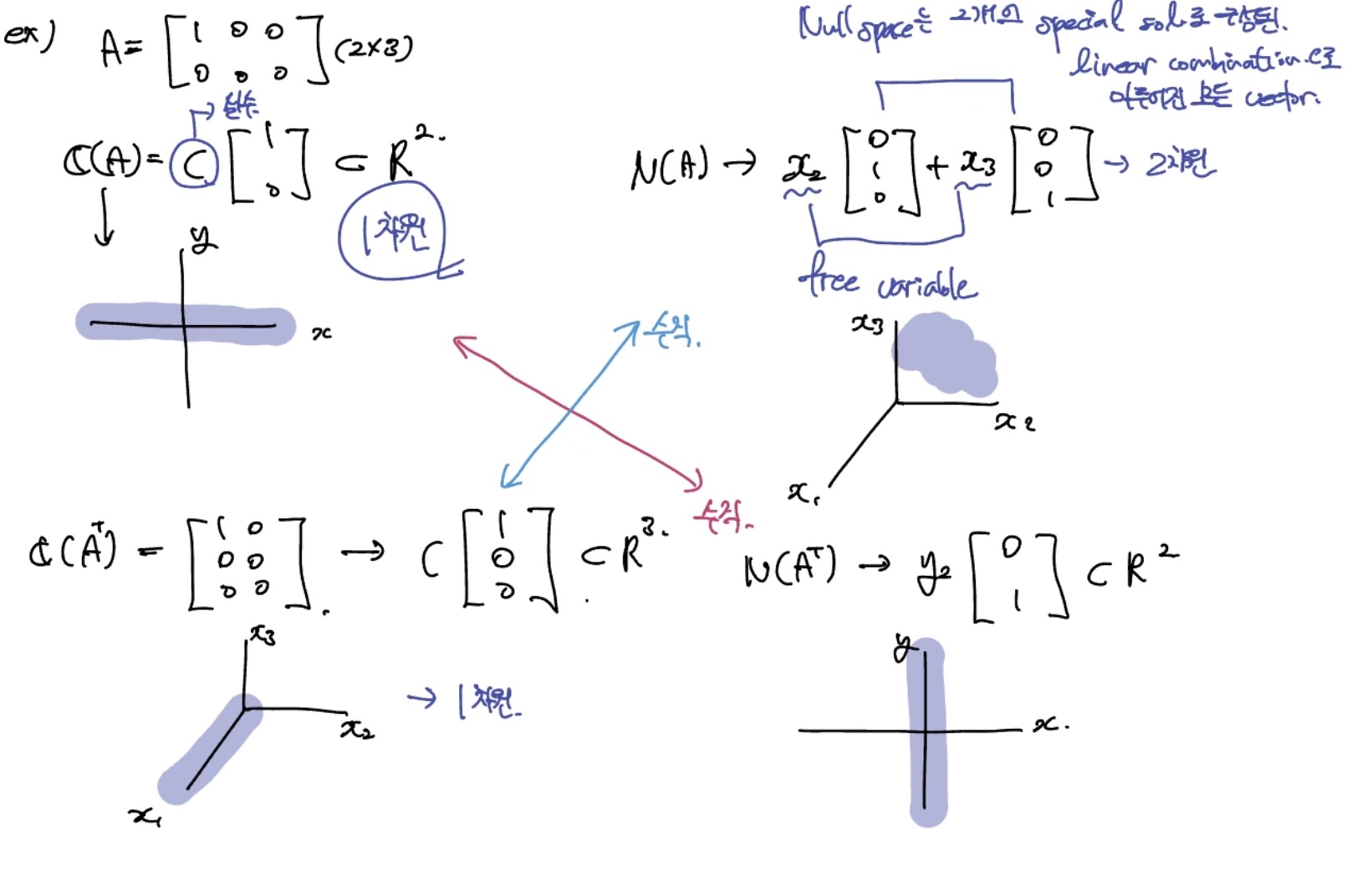
첫 번째와 네 번째는 columns space와 left null space를 의미하고 선형독립으로 이루어진 vector들만 남기고 그래프에 표기하면 수직관계임을 알 수 있다. 그리고 각 space의 dimension을 더하면 총 2차원임을 알 수 있다.
두 번째와 세 번째는 null space와 row space를 의미하고 선형독립으로 이루어진 vector들만 남기고 그래프에 표기하면 평면에 축 위에 모든 점들의 집합을 의미한다. 또한 3차원에 표기하면 서로 수직관계임을 알 수 있고 차원을 더해주면 3차원의 space임을 알 수 있다.
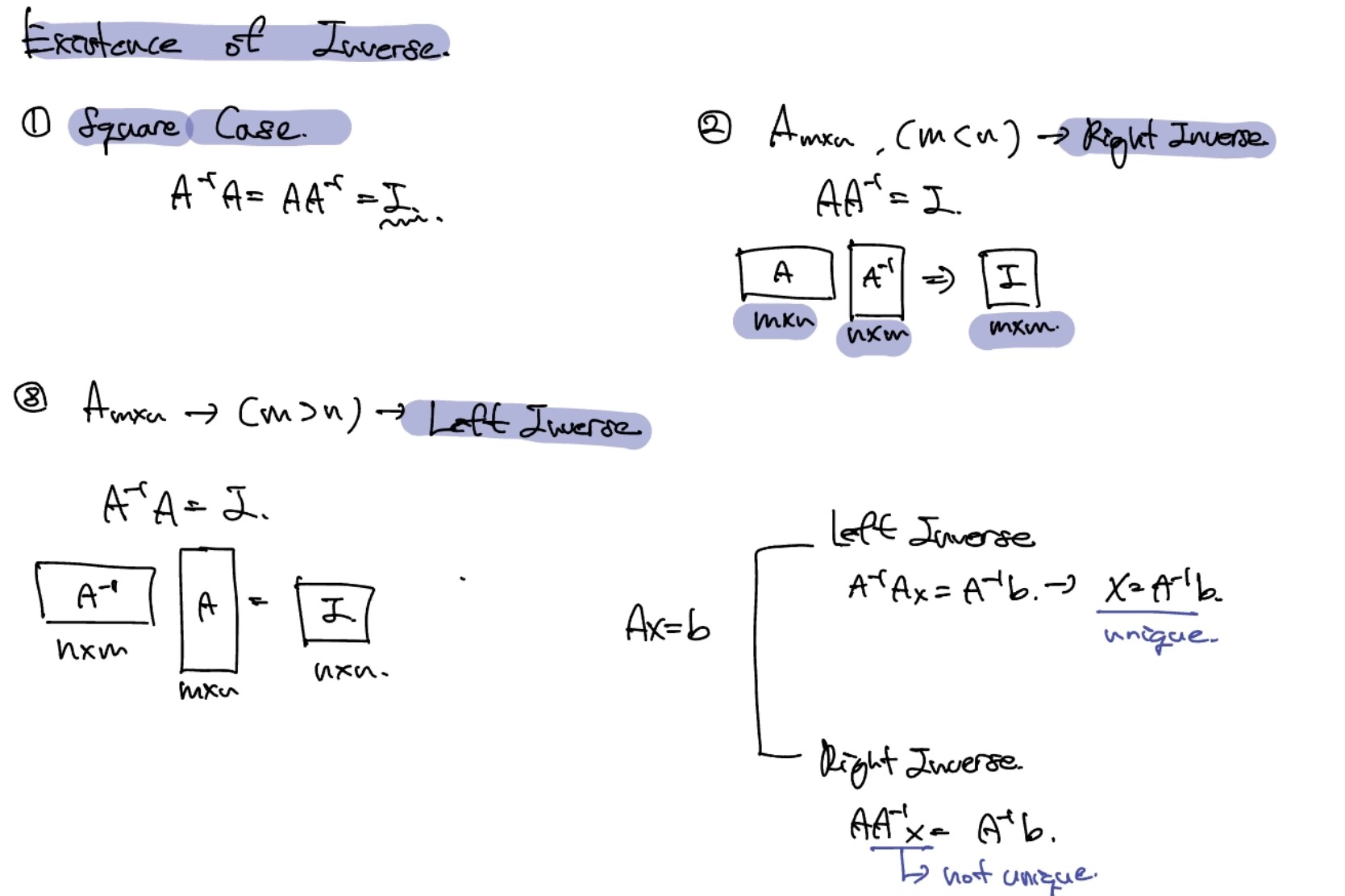
Existence Inverse
역행렬이 존재하는 3가지의 경우는 아래와 같다. 또한 left inverse때의 해는 unique하고 right inverse일 때, unique하지 않다.