GAN - Generative Adversarial Nets

0.Abstract

GAN은 기본적으로 두 개로 분리된 model이다.

• Generative Model(G) : Data의 distribution을 모사
• Discriminative Model(D) : Sample Data가 G로부터 나온 data가 아닌 real data로부터 나올 확률을 추정

이러한 두개의 model을 동시에 학습하는 adversarial process라는 생성모델 estimating을 위한 새로운 framework를 제안했다. G model를 학습하는 과정은 D model이 sample data가 G로부터 생성된 fake data인지 training data로부터 나온 real data인지 구별하는것을 실수 할 확률을 최대화 하는것이다. 이러한 framework는 minmax two-player game이라고 볼 수 있다. 본 논문에서는 임의의 G, D에 의한 함수공간상에 G가 training data의 distribution을 모사하면서 D가 training data인지 G가 생성한 fake data인지 판별하는 확률은 1/2가 된다. G와 D가 Multi layer Perceptron일 경우, 전체 syste은 backpropagation에 의해 한번에 훈련될 수 있다.

1. Introduction

딥러닝에서 우리가 다양한 종류의 data에대한 확률분포를 표현하는 계층 모델을 발견할 수 있도록 한다. 지금까지 딥러닝에서 가장 훌륭한 업적은 높은 차원에서 풍부한 sensory input data를 class label에 mapping해서 구분하는 model을 사용하는 것이었다. Well-behaved gradient를 갖는 선형 활성화 함수들을 사용한 backpropagation, dropout 알고리즘을 기반하고있다.

Deep generative model들은 maximum likelihood estimation과 관련한 model이였으며, 다루기 힘든 확률적 계산을 근사하는 것에 있어 어려움을 겪었으며, piecewise linear units의 이점을 생성적인 부분에서 가져오는 것에서 영향력이 적었다. 논문에서 소개되는 새로운 generative model은 이러한 어려움을 회피할 수 있다.

본 논문에서 제안된 adversarial nets framework에서 G는 D를 최대한 속이도록 학습되고 D는 G가 생성한 distribution인지 real data distribution인지 판별하는것을 학습한다. 이러한 경쟁적인 구도는 두 모델이 각각 objective를 달성하기 위해 스스로를 학습한다.

2. Related Work

본 논문에서 실행한 연구 이전까지 심층생성모델의 연구는 보통 확률분포함수의 parametric specification을 발견하는 것에 집중했다. 그중 DBM(Deep Boltzmann machine)이 가장 성공적인 예시이지만 intractable한 가능도 함수를 가지고있어 gradient에 대한 수치적인 근사가 필요하다. 그래서 가능도 함수를 표현하지 않고 적절한 distribution으로부터 data를 생성하는 generative machines가 발전하게됐다. 정확한 back propagation을 통해 훈련하는 Generative Stochastic Networks가 그 예시이다.

GAN은 adversarial examples와 혼동되기도 하지만, adversarial examples는 실제 data와 유사하지만 잘못 분류된 examples를 찾기위해 gradient를 기반으로 최적화된 input data를 직접 적용하면서 찾는 example이다. Adversarial examples는 사람이 구별하기 힘든 관측된 확신을 가지고 다른 class를 분류하는 neural networks에 흥미로운 결정방식을 분석하는 도구 사용된다. GAN은
adversarial examples이 사람이 구별하는 data에 대한 속성을 모방하지 않고 확신에 찬 인식을 할 수 있기 때문에 비효율적일 수 있다.

3. Adversarial Nets

Adversarial modeling은 multi-layer perceptron을 이용했다. 학습 초반에는 G가 생성한 이미지는 D가 실제인지 가짜인지 구분하는 것이 쉬워 $D(G(z)) = 0$이었다. 즉 $z$로 부터 G가 생성한 이미지가 D가 판별했을 때 바로 fake라고 판별할 수 있는것을 수식으로 나타낸것이다. 그리고 학습이 진행될수록 G는 실제 데이터의 distribution을 모사하면서 $D(G(z)) = 1$ 되도록 한다.

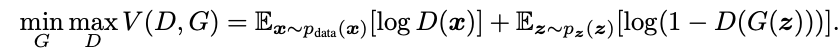
위의 식은 G가 생성한 데이터를 D가 진짜로 판별했을 때를 나타낸 식이다. 오른쪽 첫번째 항은
real data X를 D에 넣었을 때 나오는 결과를 log를 취하고 얻는 기댓값이고 두번째 항은 fake data Z를 G에 넣었을 때 결과를 $log(1-D(G(z))$ 했을 때 얻는 기댓값이다.

먼저 이 식을 D의 관점에서 봤을 때 가장 이상적인 결과를 생각해보면, D가 G에서 온 sample 데이터라면 $D(x)$가 1이 되어 첫번째 항은 0이되고 두번째 항도 0이 된다.

다음 이 식을 G의 관점에서 본다면 G가 가장 훈련이 잘되었다면 D가 구별하지 못하는 데이터를 생성한것이기 때문에 $D(G(z)) = 1$이 되고 $log(1-1) = 0$이 되기 때문에 마이너스 무한대가 되버린다.

정리하자면, 이 전체식을 maximize한다면 D의 성능이 개선되는 학습을 할 수 있고 minimize한다면 G의 성능이 개선되는 학습을 할 수 있다. 본 논문에서는 D와 G를 갖는 two-player minmax game으로 표현했다.

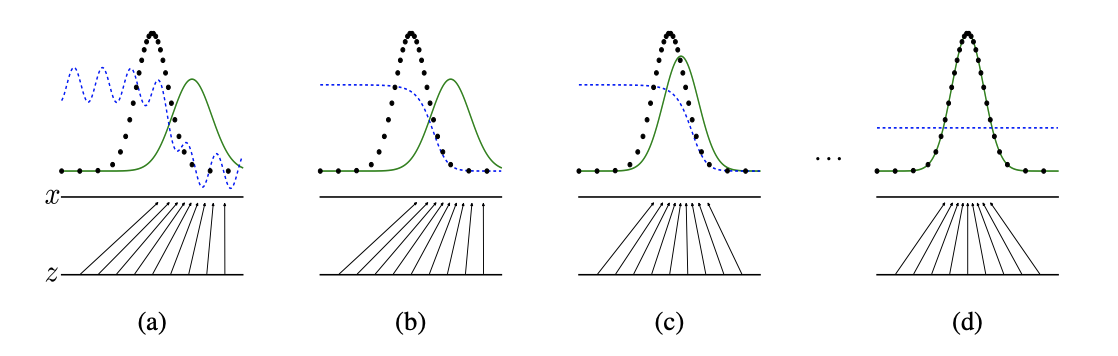
다음 그래프는 GAN의 학습과정을 나타낸것이다. (a)에서는 real data와 fake data의 distribution이 전혀 다른것을 알 수 있고 D의 성능도 좋지 않은 것을 알 수 있다(파란 점선이 D의 예측(?)). (b)에서는 D가 어느정도 예측을 하는것을 알 수 있다. (c)에서는 G는 real data의 distribution과 흡사한 fake data를 생성한것을 알 수 있다. (d)에서는 G가 결국엔 real data와 거의 흡사한 fake data를 생성하게 되고 D는 구분하지 못해 확률을 1/2로 계산하게 된다.

4. Theoretical Results

G는 $z~p_z$일 때, 얻게되는 sample data의 확률분포 $G(z)$로써 $P_{g}$를 정의한다.
GAN이 제대로 작동하려면 제안되는 Algorithm이 실제로 equation을 최적화하여 global optimum에 도달해야 한다. GAN의 mini-batch SGD 학습 알고리즘은 다음과 같다. p{g}를 p{data}에 근사시킬 수 있는지 증명하고자 한다.

GAN의 loss function을 보면 D가 G에게 gradient를 주게되고 D는 G의 선생님 역할을 하게된다. D가 G에게 가르침을 주는만큼 G도 D에게 정보를 제공하는 구조로 완벽한 D가 있다는 가정하에 $p_g$는 $p_{data}$에 수렴할 수 있다라고 증명한다.

4.1 Global Optimality of $p_g = p_{data}$

Proposition 1.

최적 상태의 D를 $D^{*}$ 라고 의미하고 G의 상태와 상관없이 p_{data}를 완벽하게 학습한 $D^{*}$의 값은 아래와 같이 나타낼 수 있다.

G가 주어진 경우 D에 대한 훈련은 $V(G,D)$를 최대화 하는것이다. 이를 통해 주어진 generator G에 대한 최적 상태의 D를 구한다.

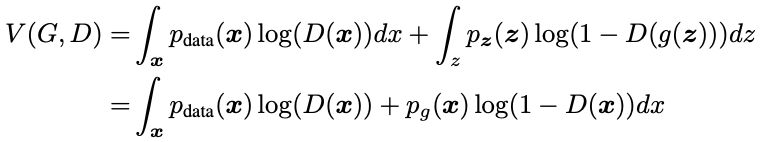
$V(G,D)$가 최대가 되기 위해선 아래의 식이 최대가 되어야하고 편미분을 통해 구할 수 있다.

G를 고정시키고 optimal한 D^{*}_G를 대입한 V(D,G)는 MLE로 해석할 수 있다. 이 때 MLE란 주어진 data를 이용하여 data를 가장 잘 표현하는 확률 분포를 찾는것으로 해석할 수 있는데 이것을 바탕으로 V(G,D)를 재구성 하면 아래와 같다.

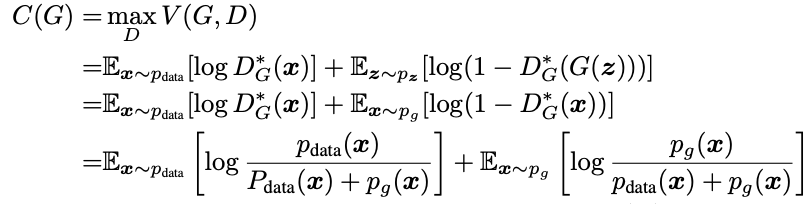
G를 고정시키고 $D^{*}$를 대입한 식이다.

Theorem 1.

$p_g = p_{data}$ 일때 C(G)는 min값이고 C(G)는 $-log4$의 값을 가진다. C(G)는 G가 최소화하고자 하는 기준이 되고 이 식의 global optimal은 $p_g$가 $p_{data}$일 때 만족한다.

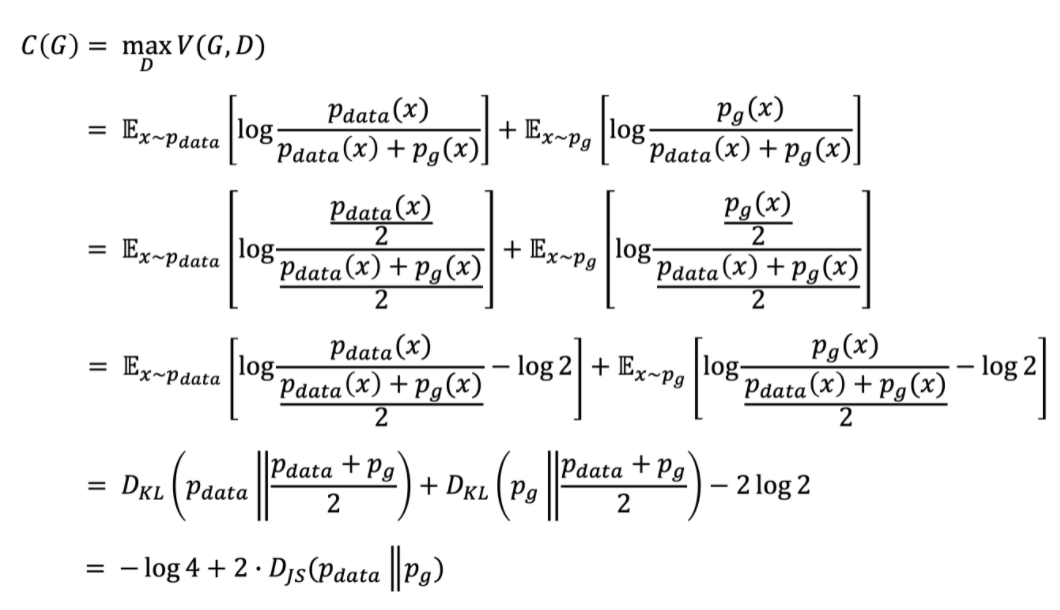
GAN의 loss 함수는 $p_g$와 $p_{data}$ 사이의 거리를 줄여나가는 방식으로 학습이 되고 거리를 측정하는 방식은 JSD였다. 두 distribution 사이의 JSD는 항상 음수가 아니고 같을 때 0이 되기 때문에 $-log4$가 global minimum임을 알 수 있다.

KL : Kullback-Leibler divergence는 p, q 두 분포사이의 차이를 측정한 값이다.

JSD : Jensen-Shannon divergence는 p, q 두 확률 분포 사이의 거리를 측정하고 같을 때 0이되고 항상 양수이다.

5. Experiments

• MNIST, Toronto Face Database, CIFAR-10에 대해 학습을 진행
• G는 rectifier linear activations, sigmoid를 혼합하여 진행
• D는 maxout activation
• D에 Dropout 적용
• 이론적인 framwork에서 noise를 허용하지 않지만, generator net 가장 하위 layer에 input으로 noise적용
• G에서 생성된 sample에 Gaussian Parzen window를 설정하고 test data 추정

G에 의해 생성된 sample들에 fitting하고 추정된 distribution에 log-likelihood를 확인하면서 test data를 추정했고 이전 model들과 비교했을 때, 충분한 경쟁력을 갖추고 있다.

6. Advantages and Disadvantages

6.1 Advantages

• Markov chains가 필요없고 gradient를 얻기 위해 역전파만 사용됨
• inference가 필요없음
• 다양한 function들이 적용될 수 있음
• Markov chains을 쓸 때 선명한 이미지를 얻을 수 있음

6.2 Disadvantages

• $p_g(x)$가 명시적으로 존재하지 않음
• D와 G의 균형이 잘 맞아야함

7. Future work

• CGAN : Class label를 추가하여 조건부 생성 모델을 얻을 수 있음
• Semi-supervised learning : 제한된 label이 있는 데이터를 사용할 때, classifiers의 성능 향상시킬 수 있음
• Efficiency improvements: G,D를 조정하는 방법이나 sample z에 대한 더 나은 분포를 결정함으로써 학습의 속도 높일 수 있음