1. Introduction
Deep Convolutional Neural Networks는 Image Classification 분야에서 많은 발전을 이끌었다. 신경망이 더 깊을수록 성능이 더 좋은것을 여러 대회에서 증명해왔다. ResNet 연구자들은 depth를 깊게하는 것만으로 성능을 향상 시킬 수 있을까라는 의문을 제기했고 간단한 실험을 했다. ImageNet보다 작은 CIFAR-10 train data를 20개의 layer와 56개의 layer를 비교했다.
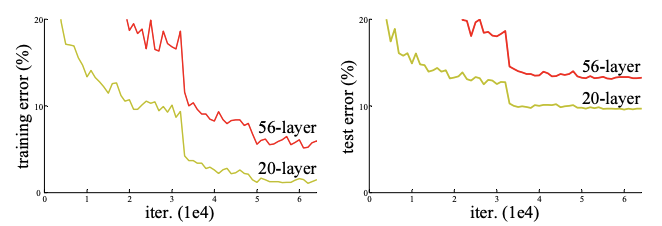
실험의 결과를 보면 일정 단계까지는 성능이 향상되었지만, 어느정도 선에서 vanishing과 exploding gradient 문제로 성능이 하락하는 결과를 보여줬다. 이러한 현상을 degradation이라고 하며, depth가 늘어날수록 accuracy가 포화상태가 되어 degrade가 가속화되는 현상이다. 이러한 현상은 overfitting의 관점에서 보는것이 아닌 depth가 늘어남에 따라 training-error가 높아지는것이다.
Degradation 현상을 해결하기 위해 normalized initialization, intermediate normalization layers을 이용할 수 있으며, 여러 layer들로 이루어진 model은 back propagation과 함께 SGD에 수렴한다. Degradation은 layer가 깊을수록 optimize 하기 어렵다는 것을 의미하며, 본 논문에서는 얕은 구조와 깊은 architecture를 고려했다. 미리 훈련한 shallow model에 identity mapping layer를 추가했지만 좋은 해결책은 아니였다. 본 논문에서는 deep residual learning framework를 도입했다. 각 layer가 기본 mapping이 되는것이 아니라 residual mapping에 적합하게 만들었다.
기존 mapping은 라면 nonlinear layer의 mapping은 라고 제시되었다. 그렇다면 기존 mapping은 의 형태로 나타낼 수 있다. 식 F(x) + x는 shorcut connection과 같고 하나 이상의 layer를 skip하게 해준다. Residual mapping에서 shortcut connection은 identity mapping을 단순하게 수행하고 output을 다음 stack layer의 output에 추가된다. Identity short connection은 추가적인 parameter도 필요하지 않고 복잡한 compute도 필요하지 않다. 전체 network는 backpropagation과 함께 SGD에 의해 end-to-end로 학습한다.
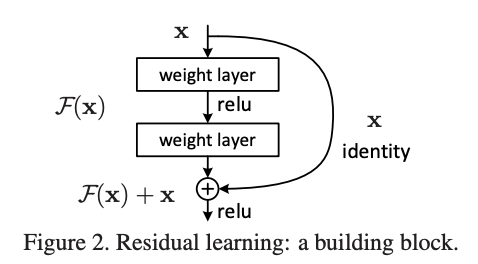
Input x가 model의 F(x)의 과정을 거치면서 identity가 더해지면서 output으로 F(x) + x가 나오게 된다.(x는 identity)
본 논문의 목표 두가지는 다음과 같다.
-
Plain net과는 다르게 residual net이 더 쉽게 optimize할 수 있다.
-
Residual Net이 더 쉽게 accuaracy를 높일 수 있다.
1. Deep Residual Learning
1.1 Residual Learning
가를 기존 mapping으로 간주하면 input 가 다수의 nonlinear layer가 복잡한 함수를 점근적으로 근사할 수 있다고 가정할 때, residual function을 점근적으로 근사할 수 있다(?)
1.2 Identity Mapping by Shortcuts
ResNet은 적은 layer의 수라도 residual learning을 적용한다.
는 input이고 는 output vector이고 는 residual mapping을 의미.
위의 식을 model로 재구성 한다면 가 된다. 또한 F와 x의 차원을 맞춰주어야한다.
Extra parameter와 computational complexity가 필요없는것이 residual network의 장점이다.
1.3 Network Architectures
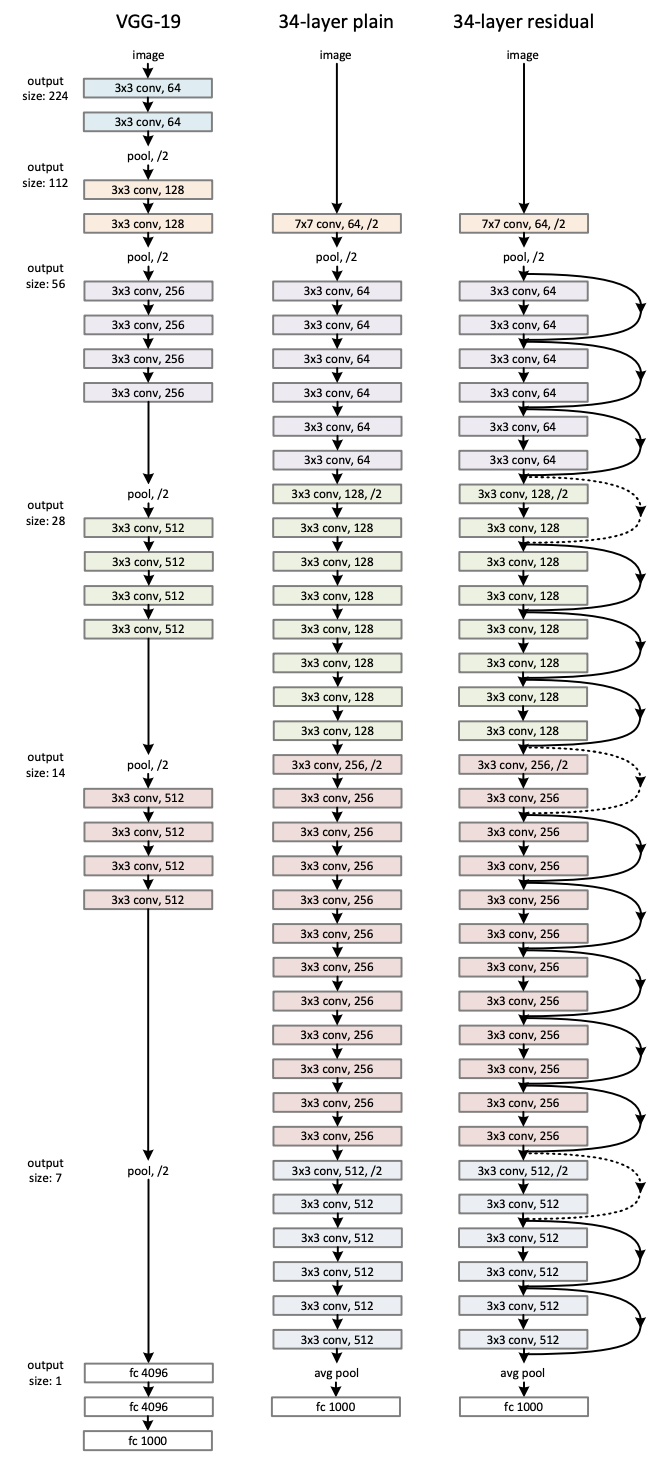
Plain network와 residual network를 비교하기 위해 ImageNet data를 사용.
Plain Network
Plain Network는 단순히 layer를 깊게 쌓은 구조이다. Conv layers는 다음과 같은 규칙을 가지고 있다.
- 3x3 filters
- 각 layer는 같은 크기와 같은 수의 output feature map을 가지고 있음.
- feature map size가 반으로 축소된다면, 한 layer당 time-complexity를 유지하기 위해 filter의 수는 두배가 됨.
Conv-layer에서 stride가 2로 downsampling을 진행하고 model의 마지막엔 global average pooling layer, 1000-way의 fully-connected layer, softmax를 사용했다. 총 34개의 layer로 구성되어 있고 이 model은 VGG net보다 filter의 개수가 많고 복잡도는 낮다.
Residual Network
Plain Network를 기반으로 하며, shortcut connections를 추가했다. Input과 Output의 dimension이 같다면 바로 identity shortcuts을 사용할 수 있다. Dimension이 증가할 때 두가지를 생각할 수 있다.
- Zero padding을 추가하여 size를 맞춘다.(parameter가 추가적으로 발생하지 않음.)
- Projection을 이용하여 size를 맞춘다.
1.4 Implementation
ImageNet data를 적용시켜 다음과 같이 설정.
- Image resize : 224 x 224
- Batch Normalization 사용
- Initialize Weights
- SGD
- Mini Batch : 256
- Learning Rate : 0.1
- Iteration : 60 * 10^4
- Weight Decay : 0.0001
- Momentum : 0.9
- No dropout
2. Experiments
2.1 ImageNet Classification
1000개의 class를 가진 ImageNet 2012 classification dataset을 사용했다. 128만장의 training images를 사용했고, test를 위해 5만장의 validation images를 사용/ 그리고 10만장의 test image를 사용하여 결과를 냈다.
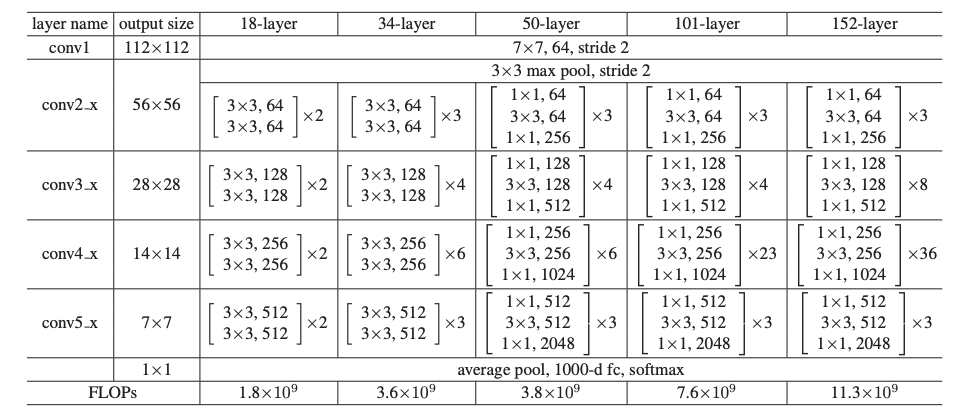
Plain Net의 경우 34-layer가 18-layer보다 성능이 안좋은걸 확인했었는데, 이것은 Batch normalization을 사용한 결과여서 vanishing gradient 때문이라고 보기 어렵다.
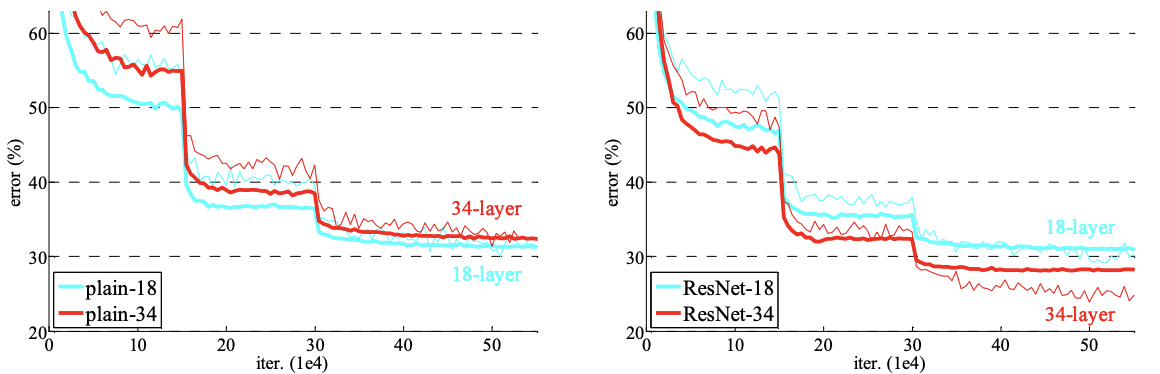
모든 shortcuts을 위해서는 identity mapping을 사용했고, dimension을 맞추기 위하여 zero-padding을 이용했다.
그래프를 보면 plain net은 34-layer가 더 낮은 성능을 보이지만 ResNet은 34-layer가 성능이 더 좋았다. Degradation문제가 해결된 것으로 보인다.
Identity vs Projection Shortcuts
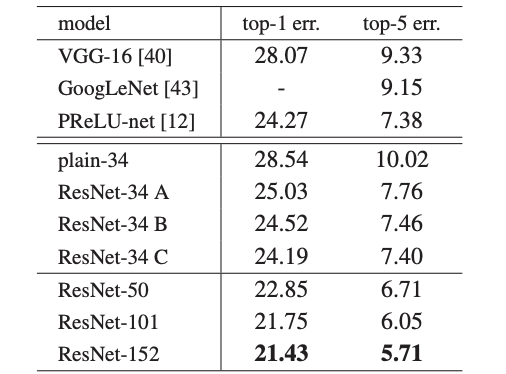
3가지의 option을 비교했다.
- Dimension 증가를 위해 zero-padding을 사용
- Dimension 증가를 위해 projection shortcuts을 사용
- 모든 shortcuts들이 projection인 경우
성능은 모든 shorcuts들이 projection인 경우가 제일 높았다. 각 경우들의 차이가 적은것을 보면 rojection shortcuts을 사용하는것이 필수적이라고 보이지는 않는다.
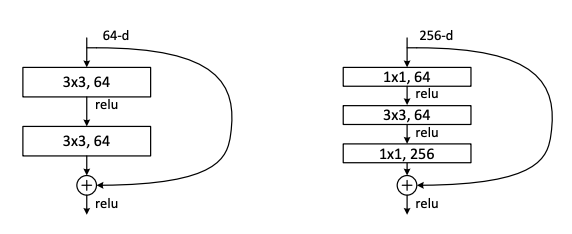
위 model은 학습시간을 고려하여 Bottleneck 구조를 사용한다. 각각의 residual function은 3겹으로 쌓았고, 1x1 dimension을 감소시키고 복원하는 역할을 하면서 3x3이 더 적은 input과 output을 갖게한다.
두개의 complexity도 비슷한데 이 과정이 projection으로 바뀌게되면, time complexity와 model size가 더 커진다.
Analysis of Layer Response
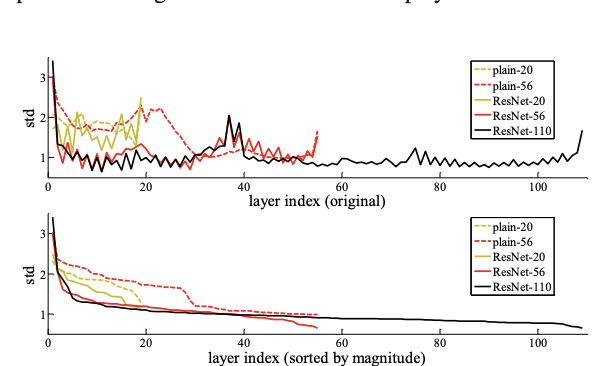
Plain Net과 ResNet의 layer에서 response의 표준편차를 확인했다. 위의 그래프를 보면 ResNet의 response가 더 작은것을 확인할 수 있다.
Exploring Over 1000 Layers
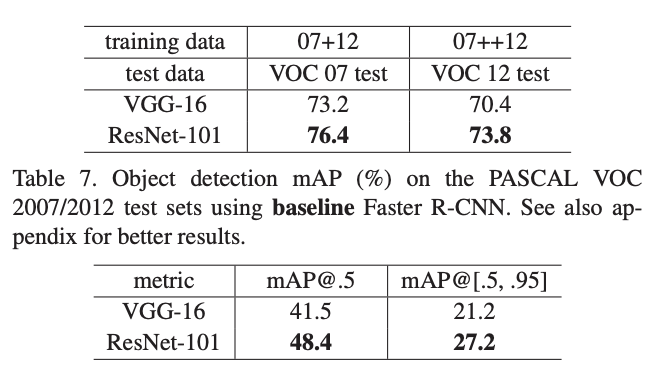
1202-layer network에서는 110-layer network와 비슷한 training error를 보였지만, 성능은 낮았다. 본 논문에서는 dataset의 크기에 비해 layer가 너무 많아서 overfitting 때문이라고 했다.