Transformer

Introduction

Transformer는 2017년 구글이 발표한 "Attention is All You Need" 논문에서 나온 model로 기존의 seq2seq의 구조인 encoder-decoder와 attention mechanism만으로 구현된 model이다.

Architecture

Seq2Seq Encoder-Decoder

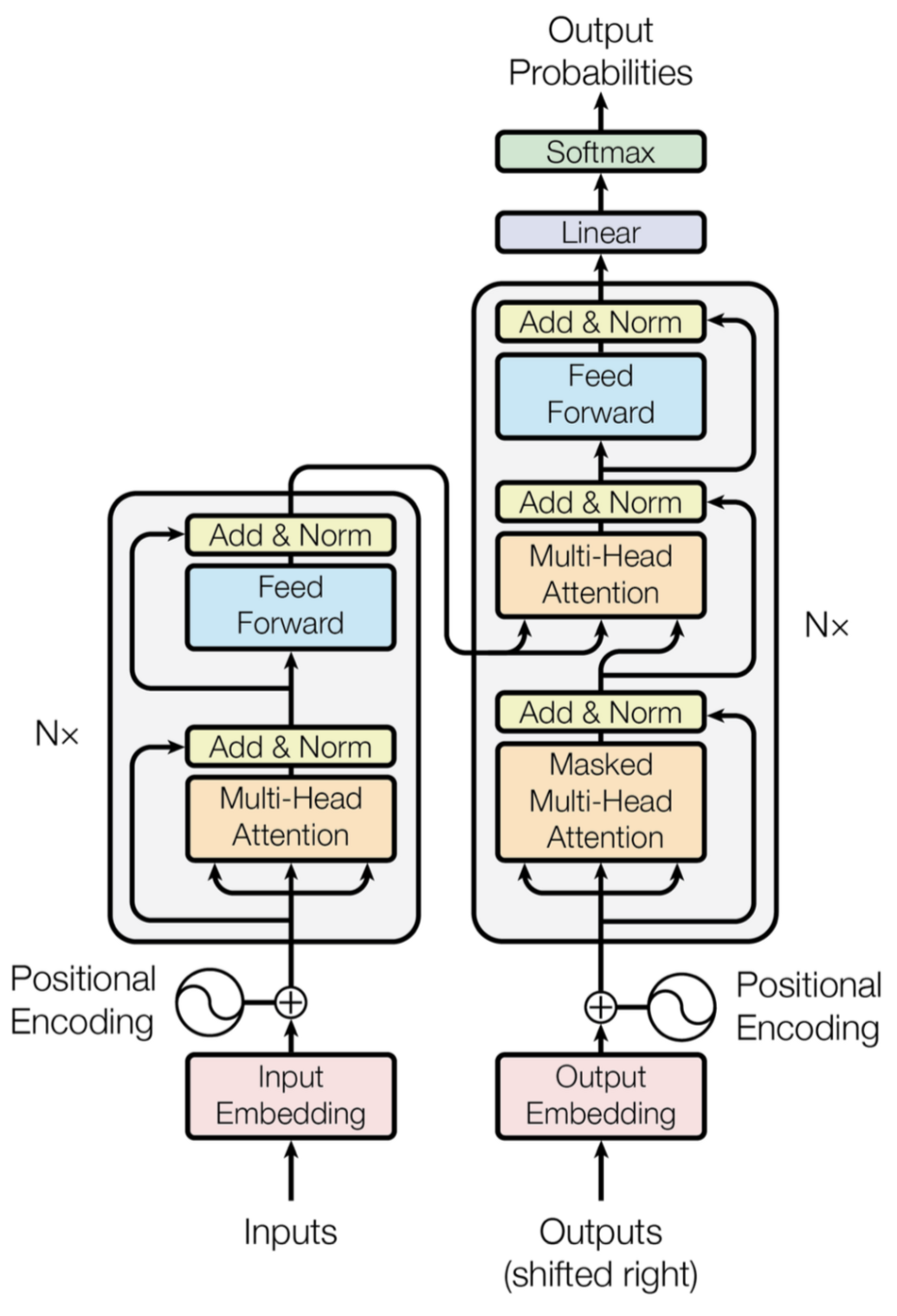
기본적으로 seq2seq과 같이 인코더-디코더 모델의 구조를 가지고 있다. 그리고 이전 RNN기반의 seq2seq구조에서는 encoder와 decoder에서 RNN이 t개의 시점을 가지는 구조였지만 transformer에서는 N개로 구성되고 있다.(그림에서는 6개)

Transformer의 정해진 입력과 출력의 크기는 512이다. Embedding vector의 차원 또한 512이다.

Encoder Stacks

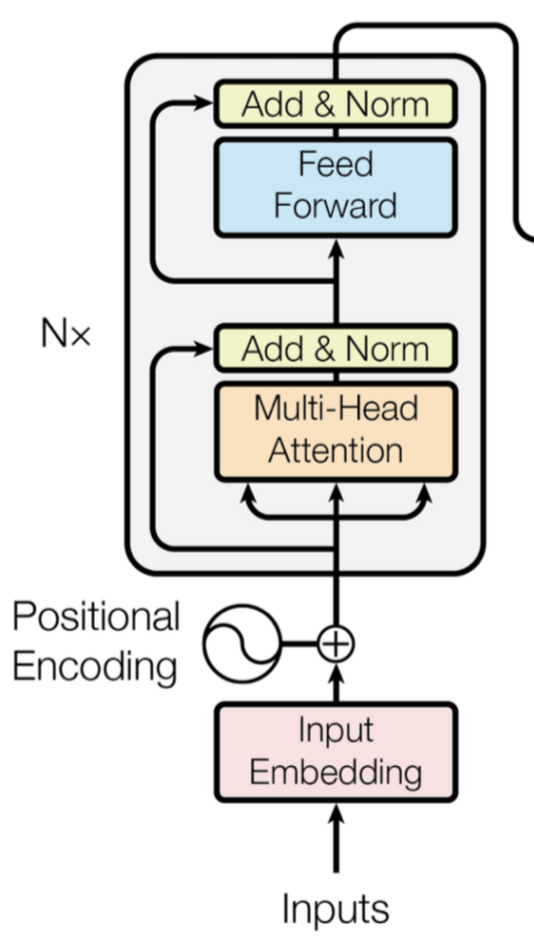
먼저 encoder는 총 6개로 구성되어 있고 하나의 encoder에는 2개의 sub-layer로 구성되어있다.
Multi-head attention은 self-attention이 병렬적으로 여러개 나열되어 있는 layer이다.

Transformer의 encoder에서는 먼저 input으로 들어오는 text를 embedding한다. 이러한 input embedding과 positional encoding을 element wise로 더하여 attention layer에 입력된다.

Positional Encoding

Transformer의 구조에서 Positional Encoding이 필요한 이유는 transformer에서는 순서 정보를 갖고있지 않기 때문이다. Positional Encoding은 단어의 위치를 알려줄 수 있는 vector이다.

두개의 함수, cos함수와 sin함수를 이용하여 홀수, 짝수에 따라 사용한다.

두가지 함수를 사용하는 이유는 위치가 커질 때마다 (멀어질 때마다) 그 값이 다시 작아져(주기 함수의 특성) 어떤 두 단어의 위치 값이 같아지는것을 방지하기 위해서다. Cos함수와 Sin함수를 사용하면 값들을 증가/감소로 표현할 수 있으며 선형 변환으로 표현이 가능하다.

pos는 각 단어의 번호이고 i는 embedding 값의 위치이다. 아래 그림처럼 positional encoding 값을 구하고 구한 embedding값과 더해준다.

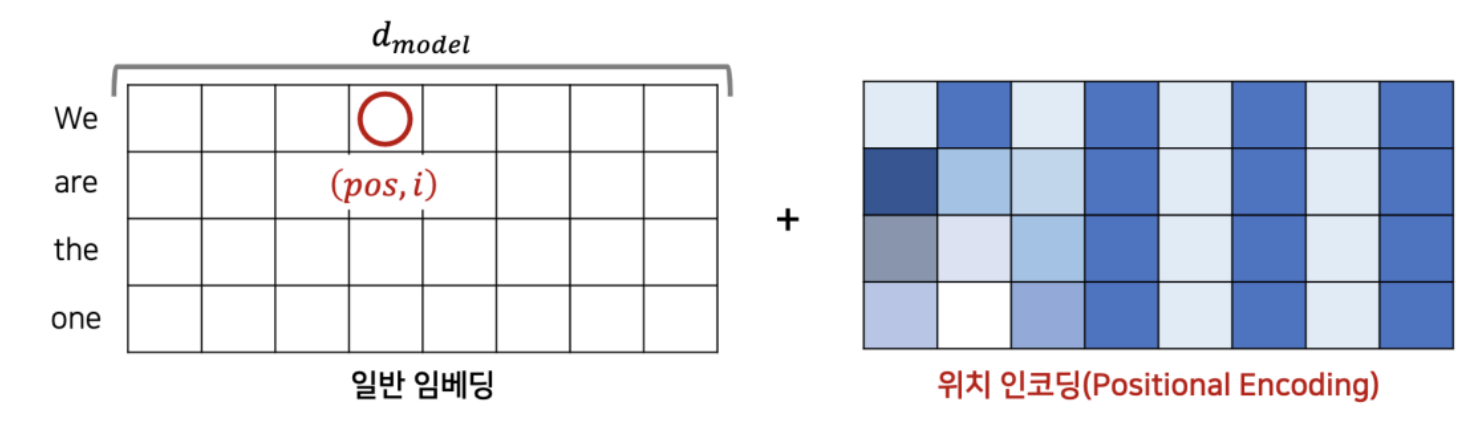
Positional Encoding을 통해 위치정보를 얻으면 단어간의 거리가 멀다면 Positional Encoding값도 멀어지게된다.

예시로 10개의 positional encoding과 10차원으로 만든 matrix를 표현하면 다음과 같다.

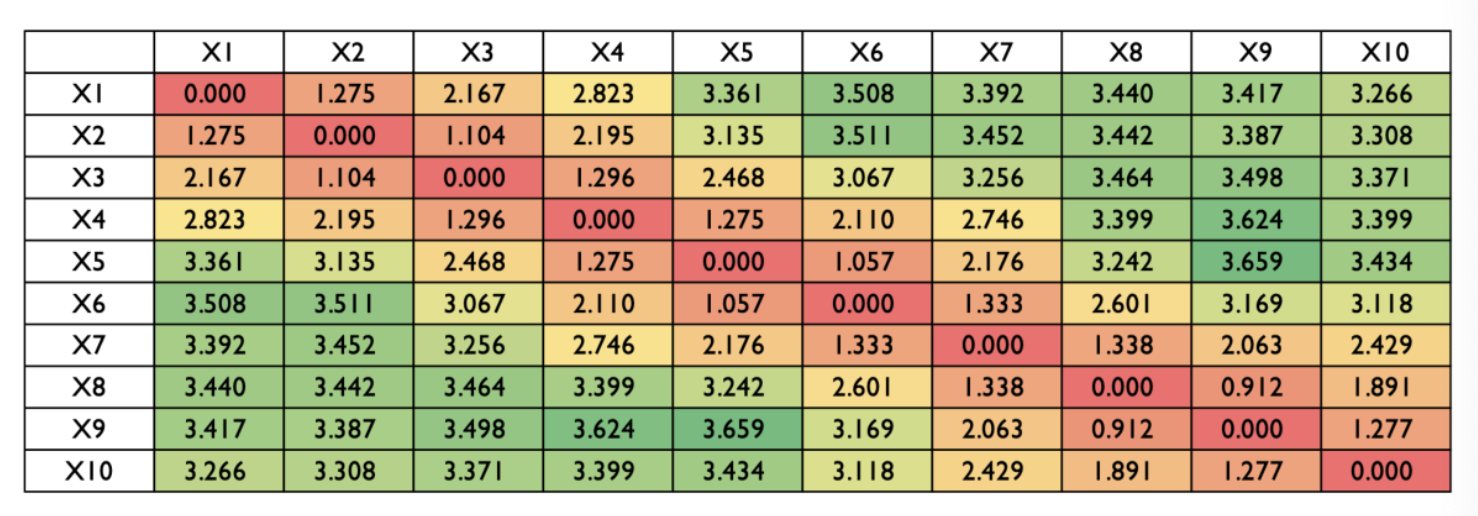
단어 사이의 거리가 멀수록, 대각행렬에서 멀어질수록 값이 커지는것을 알 수 있다.

Positional Encoding을 시각화하면 아래와 같다.

위 그림에서 빨간색의 대각선은 당연히 모두 값이 0이고, 노란색 -> 초록색 순서로 값이 커진다, 즉 거리가 멀어진다는것을 확인할 수 있다.

주대각성분의 값은 0을 갖고 색이 옅을 수록 거리가 멀다는 뜻이고 대각행렬성분은 자기자신과의 거리를 뜻하므로 진한색의 대각선으로부터 멀어지면 색이 옅어지는것을 알 수 있다.

Self-head Attention

다음은 self-head attention이 어떤 mechanism을 가지고 있는지 알아봤다. 만약 지시대명사가 문장안에 존재할 경우 model이 무엇을 가르키는지 어떻게 알수있을까? Self-head attention을 이용하면 알 수 있다. Model이 입력 문장 내의 단어를 처리하면서 self-attention을 이용해 문장 내의 다른 위치에 있는 단어들을 보고 연관이 있는 단어를 찾아줄 수 있다.

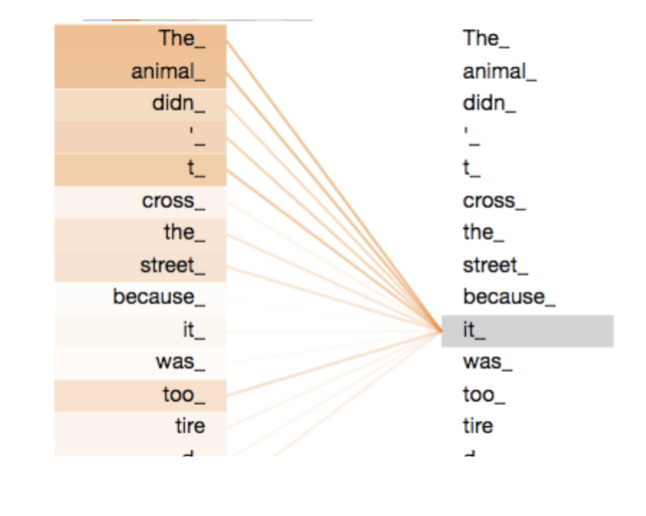
Self-Attention mechanism을 이용해 'it'이라는 단어가 'animal'에 attention을 많이 받는것을 알 수 있다.

Self-attention의 첫번째 단계는 encoder에 입력된 vector들에게서 3개 vector를 만드는 것이다. 단어의 Query vector, Key vector, Value vector를 만든다.

Query : 현재 단어의 representation
Key : Query와 비교할 단어의 representation
Value : attention mechanism을 이용해 가져올 representation

이 vector들은 각 3개의 가중치 행렬과 곱함으로써 생성된다. 여기서 input vector의 차원보다 이 3개의 vector들의 차원이 낮게 설정되는데 그 이유는 Multi-head Attention의 각 head에서 연산된 결과를 concat할 때 계산 복잡도를 낮게해주기 위함이다.

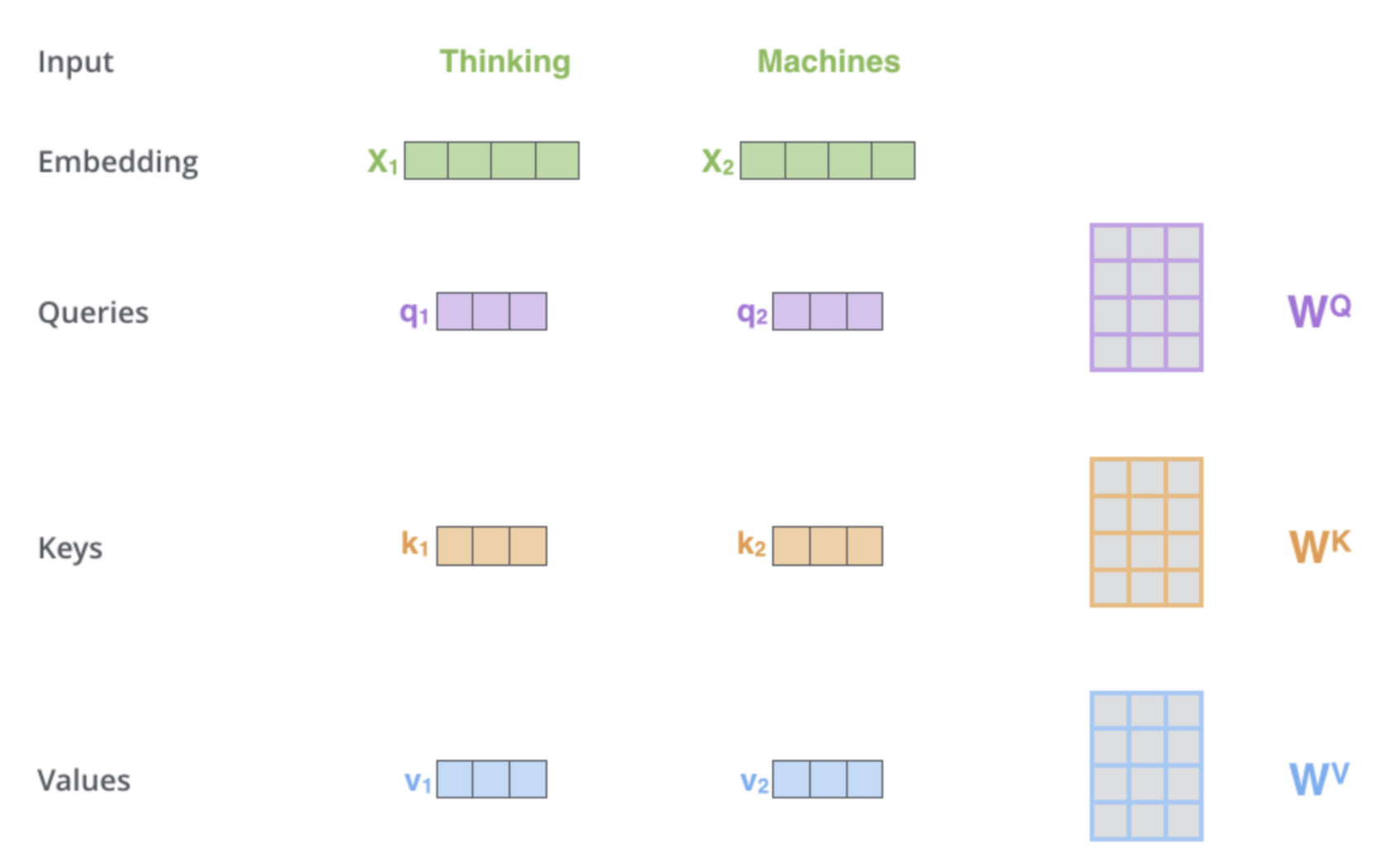
X1에 weight matrix인 $W^Q$를 곱해 query vector인 $q_1$을 생성한다. 그리고 다른 input
vector인 X2와 $W^Q$를 곱해 $q_2$를 생성한다.이러한 방법으로 query, key, value vector를 생성할 수 있다.

두번째 단계로는 attention score를 계산하는 단계이다. 우리는 모든 문장안에 존재하는 단어들의 점수를 각각 계산해야된다. 이때 이 attention score는 현재 단어의 query vector와 비교할 단어의 key vector의 내적으로 계산된다. 그렇다면 첫번째 attention score는 $q_1$과 $k_1$의 내적값일 것이다. 그리고 두번째 attention score는 $q_1$과 $k_2$의 내적값이다.

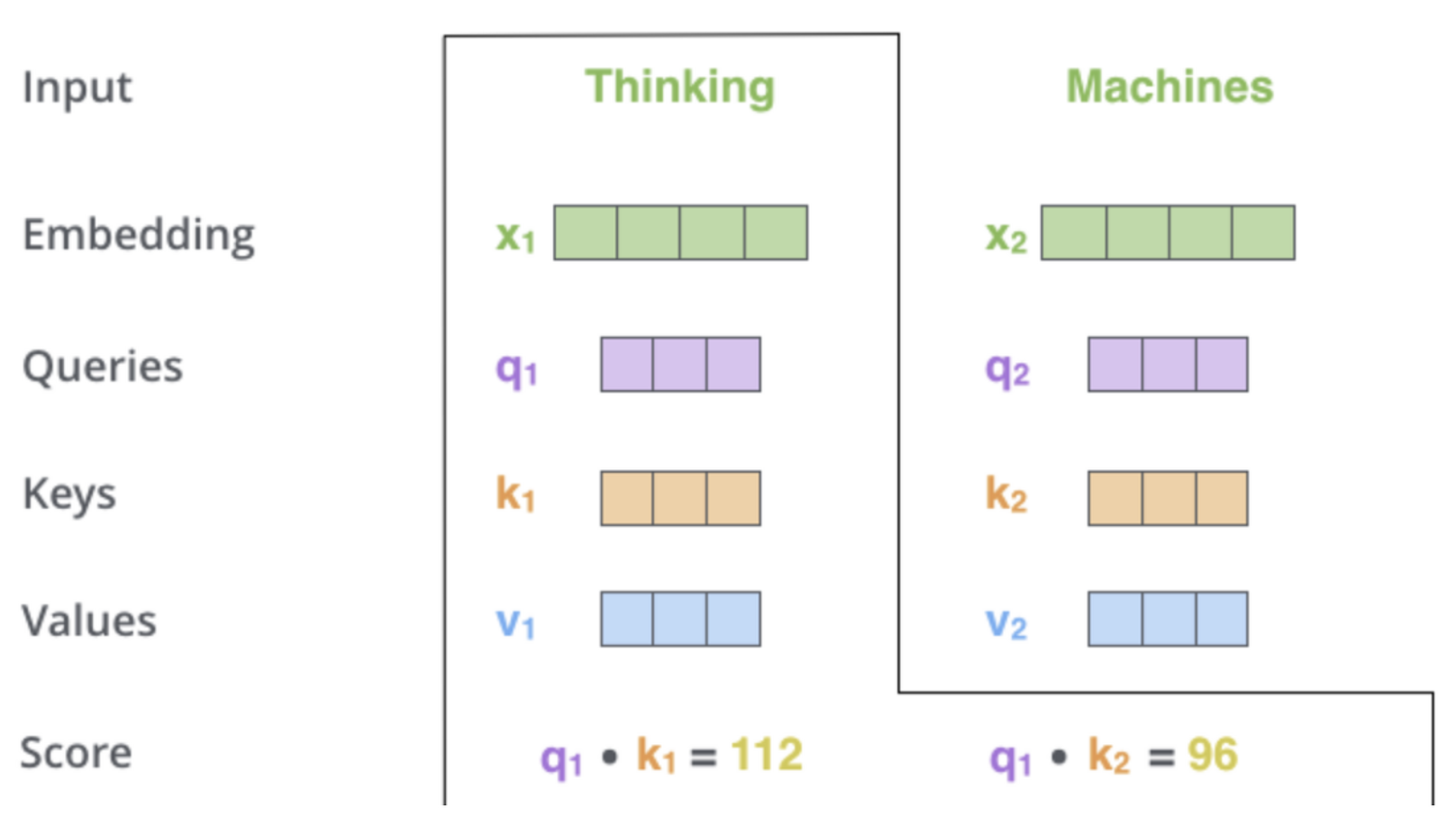
세번째 단계는 이 점수들을 $\sqrt{d_k}$로 나누는 것이다. 이러한 scaling을 통해 안정적인 gradient를 가질 수 있고 다음으론 softmax 함수를 통과시켜 모든 점수들의 합을 1로 만들어준다.

다섯번째는 softmax를 거쳐 나온 점수를 value vector와 곱하는것이다. 그렇게되면 attention score값이 높은 단어는 남게되고 없는 단어는 아주 작은값으로 표현된다.

마지막 단계는 이렇게 나온 weighted value vector들을 다 합하는것이다. 이것이 self-attention layer의 최종 output이다.

multi-head attention

본 논문에서는 self- attention과 multi-head attention을 같이 사용했다. 그렇다면 attention layer가 여러개의 representation 공간을 가질 수 있게 된다. 본 논문에서는 8개의 attention heads를 이용했는데 그렇다면 encoder, decoder 각각 8개의 attention layer를 갖게되는것이다. 각각 모두 서로 다른 query, key, value의 weight matrix를 가지고 있다.

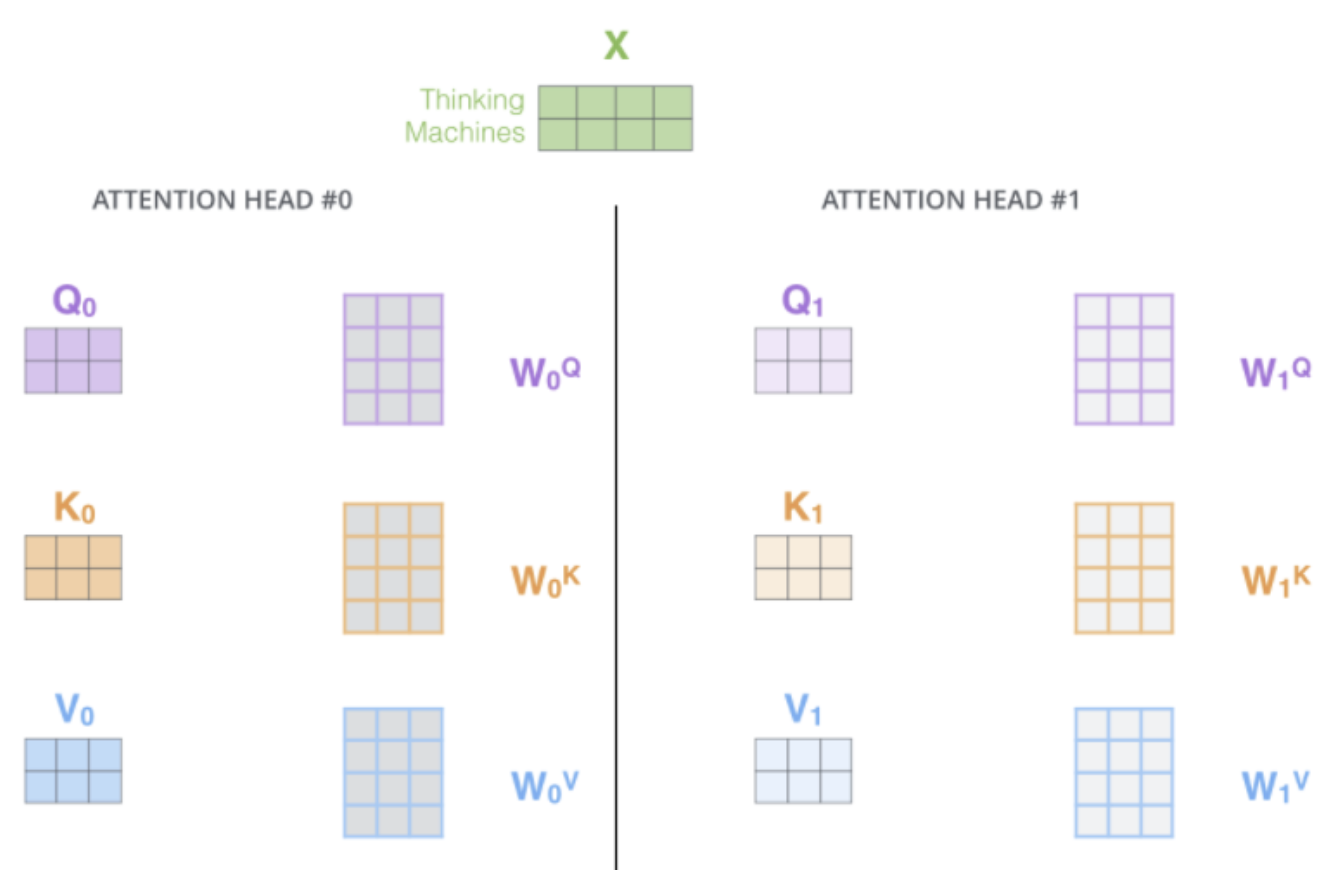
각 head에 다른 query, key, weight matrix을 가지게 되고 앞서 설명한 연산을 통하여 8개의 최종 output을 갖게된다.

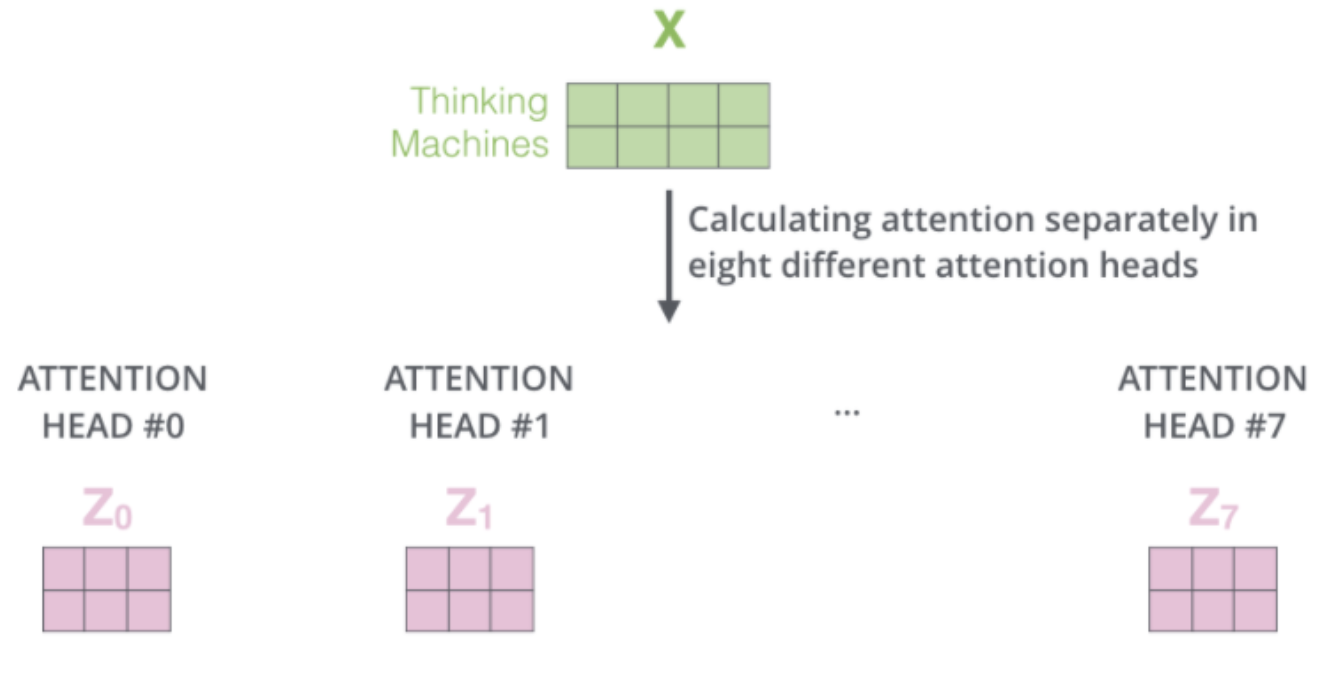
그러나 이 8개의 Z행렬을 바로 feed-foward layer로 보낼 수 없다. 그래서 8개의 행렬을 모두 concat하고 다른 하나의 weight matrix를 곱한 다음, feed-foward layer로 보낸다.

The Residuals

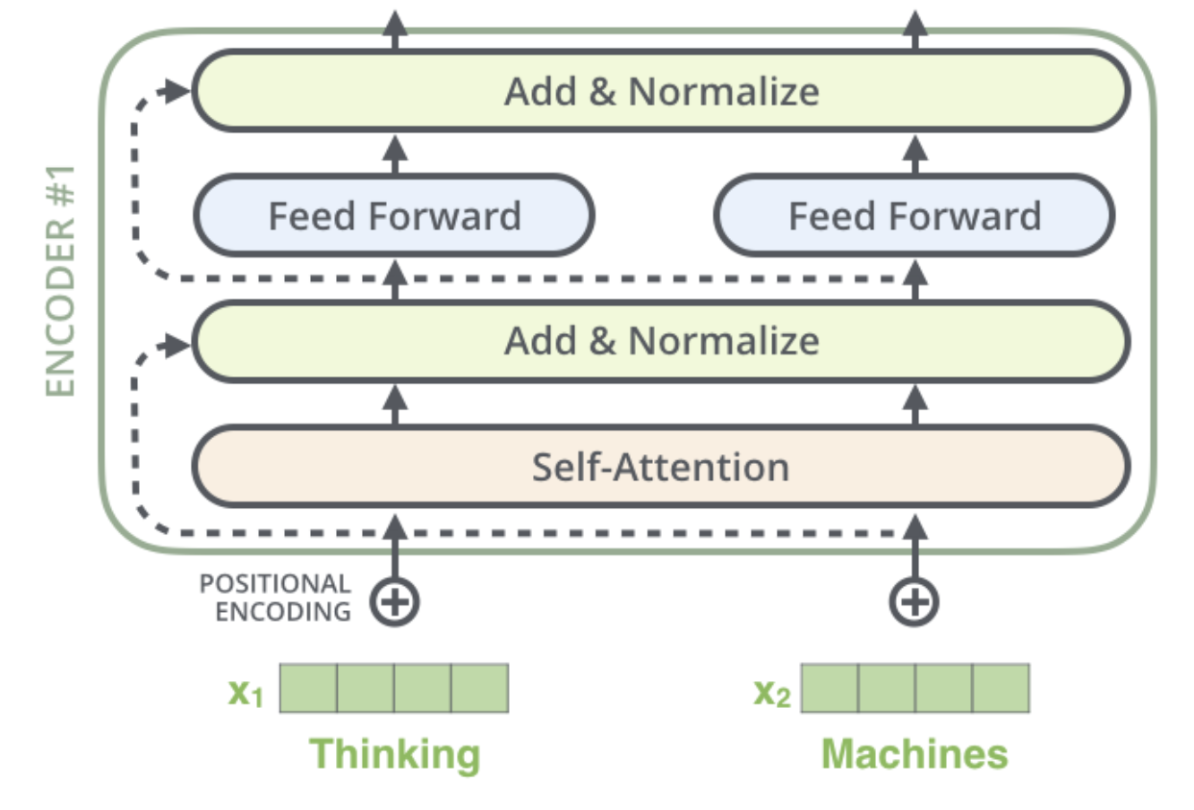
각 encoder의 내부는 sub-layer 두개가 모두 residual connection으로 이루어져 있고 그 이후에는 layer-normalization을 거치게 된다.

먼저 Residual Connection은 비선형 함수의 output에 기존 input을 더해주는 형식이다. 예를 들어, $f(x)$는 layer를 많이 거칠수록 gradient가 vanshing 될 수 밖에 없는데 이때 $f(x) + x$의 형태를 가지면 1의 gradient는 보장되기 때문에 안정적인 학습이 가능한다.

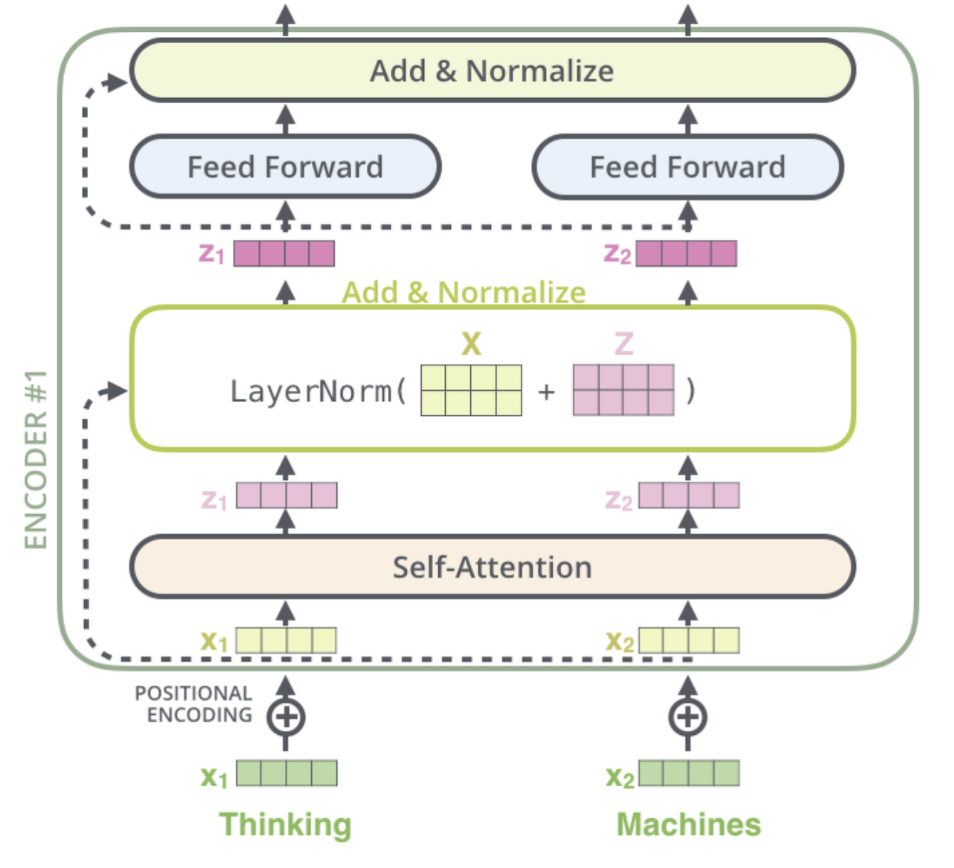
위 그림에서 보다시피 encoder의 제일 처음 부분에서 우리는 positional encoding과 embedding vector를 더했는데, positional encoding vector는 gradient vanshing이 일어날 수 있기 때문에 attention layer를 스킵하고 다음 layer로 이동한다. 이렇게 positional encoding과 attention layer의 output인 Z와 더해줘서 layer normalization을 적용한다.

Position-wise Feed-Foward Networks

다음으로는 feed-foward networks가 있는데 각 position마다, 다시 말하면 각 단어마다 적용되기 때문에 position-wise라고 할 수 있다. Network는 두개의 linear transformation과 activation function ReLU로 이루어져 있다.

$x$에 선형변환을 적용하고 ReLU 함수를 거쳐 다시 한번 선형변환을 해준다. 같은 encoder block 내에서의 $W_n$의 값은 모두 같지만 각 block마다는 다른 값이다.

Decoder Stacks

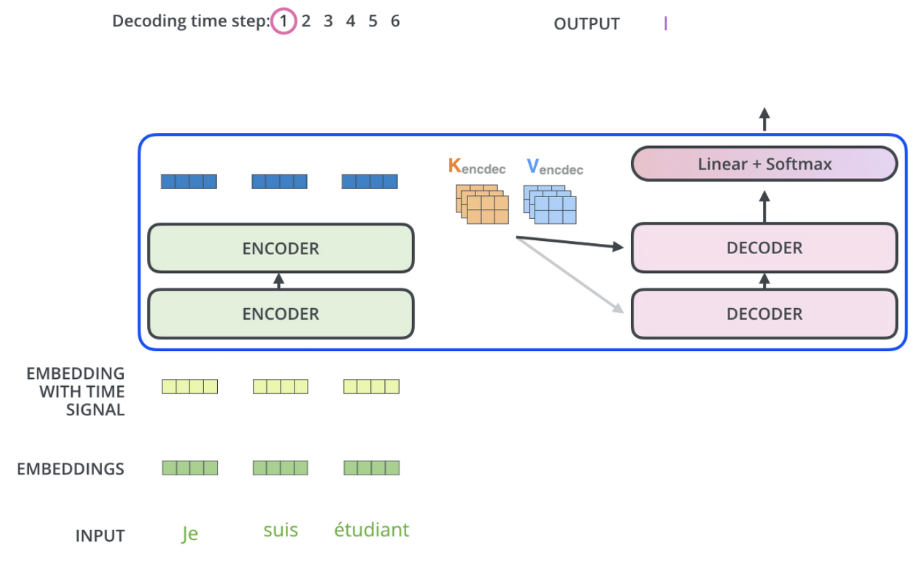
Decoder block에서는 각 step마다 token(target word)하나를 출력하게되고 마지막을 알리는 < EOS > token이 출력될 때까지 반복한다. 각 time-step의 output token은 다음 step의 decoder의 input으로 들어가게된다. Encoder와 똑같이 input이 embedding layer를 거치고 positional encoding값도 더해지게 된다.

Masked Self-Attention

Decoder의 self-attention은 encoder와는 다르게 작동하는데, 이전의 정보들만 가지고 다음 token을 예측해야한다.

• 즉 inference과정에서 생성되지 않은, 미래시점의 token에 대해서는 attention 연산을 거치지 않음.

그 이외에는 self-attention과 multi head attention이라는것과는 같다.

Decoder의 self-attention layer는 output sequence 내에서 현재의 위치 이전의 위치들에 대해서만 attend하여야 한다. 그래서 현재 스텝 이후의 위치에 있는 값들에 masking을 함으로써 가능하다. 그리고 다른 차이점은 Query matrix는 밑에 layer에서 가져오고 key와 value는 encoder의 output에서 가져온다는 점이다.

The Final Linear and Softmax Layer

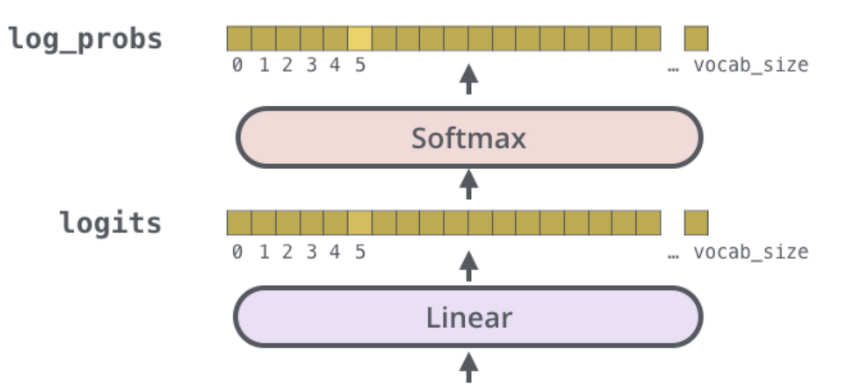
여러개의 decoder block를 거치고 난 vector는 linear layer를 거치게 된다. Linear layer는 fully-connected neural network로 input으로 들어온 vector를 logits vector로 projection하게 됩니다. 그리고 이 logit vector가 softmax layer를 거치게 되면서 더하면 1인 확률로 변환시킨다. 가장 높은 확률을 가지는 cell에 해당하는 단어가 최종 해당 step의 output이 된다.