요약
사람의 기보를 바탕으로 다음 수를 학습하는 SL policy, 작은 network rollout policy, SL policy를 RL로 학습한 RL policy, value network 4개로 구성
RL policy의 기보 중 독립성을 위해 1개의 state와 win여부를 토대로 value network를 학습.
이후 MCTS를 진행하는데
Tree를 구축해서 node를 따라서 진행하면서 더 정확한 value를 얻기 위해서 여러가지 수를 계산해본다.
이때 value network의 value와 rollout policy를 끝까지 진행해서 얻은 값의 비율합으로 value를 평가
가장 visit이 많은 action을 선택
Abstract
바둑은 경우의 수가 천문학적으로 많다. 그래서 기존의 경우의 수가 그나마 적은 체스와 같은 다른 보드게임 분야에 비해서 인공지능이 활약하기 매우 어려웠다.
하지만 구글 딥마인드에서 이세돌 9단을 알파고가 이기면서 바뀌었는데
이 논문은 알파고의 원리에 대한 논문이다.
간단하게 몬테카를로 트리 서치(MCTS)를 통해서 사람처럼 스스로 미래의 수를 계속 둬보는 것이 중심이다.
1. Introduction
모든 게임은 각 board state s에 대해서 게임의 승패를 결정하는 optimal value function 가 존재한다
그러나 state space가 매우 크면 이를 구하기 매우매우 어려워지는데 기존의 체스의 경우 즉 breadth의 depth승이 이었지만 바둑의 경우 으로 어마어마하게 크다.
이를 모두 다 고려하는건 우주의 나이만큼의 시간이 있어도 불가능하다.
그렇기에 효과적으로 탐색을 진행을 해서 모든 경우를 다 탐색하지 않게 하는 것이 중요한데
- depth는 position evaluation으로 줄일 수 있다. 즉 기존 강화학습에서 value의 근사 로 빠르게 평가해서 더 깊은 depth를 탐색하지 않게 한다.
- breadth는 policy 에서 확률 분포를 뽑아내고 샘플링을 진행함으로써 줄일 수 있다.
이 논문에서는 monte carlo tree search(MCTS)를 통해서 정확한 value를 근사를 하였고 이때 각 policy가 action을 진행하면서 tree를 점점 늘려간다.
이때 policy는 convolution을 사용 board를 19x19의 이미지로 보고 진행할 수 있기 때문
네트워크는 4개로 구성이 된다.
- supervised policy network : 사람이 둔 수로 supervised
- fast policy : 혼자 빠르게 두기 위한 network
- RL policy : Supervised를 가져와서 혼자 학습하며 강화학습
- value network : value를 평가하기 위한 network. RL이 둔 수를 가지고 누가 이기는지 예측하는 식으로 학습
로 구성이 된다.
그림은 다음과 같다.
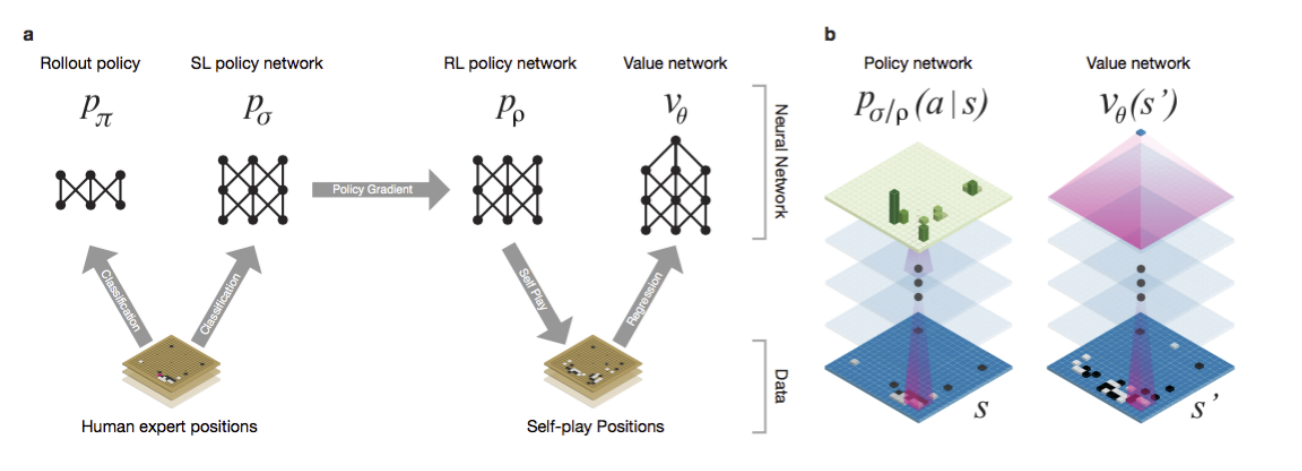
Supervised Learning of Policy Networks
supervised policy에 대한 설명으로 특정 state 를 주고 사람이 어디에 두었는지를 예측하는 식의 supervised learning을 진행한다.
SL policy 로 표기가 된다.
논문에서는 13 layer의 network이고 3천만 개의 데이터로 학습이 되었다고 한다. 학습시에는 데이터를 그냥 독립적으로 sampling해서 state를 주고 action을 예측하는 식으로 진행
테스트 결과로는 사람의 feature engineering이 추가되면 전문가의 수를 57% 예측하고 board 그 자체로는 55%의 성능이 나왔다고 함.
이때 예측 확률이 높을수록 승률이 높아졌다고 함.
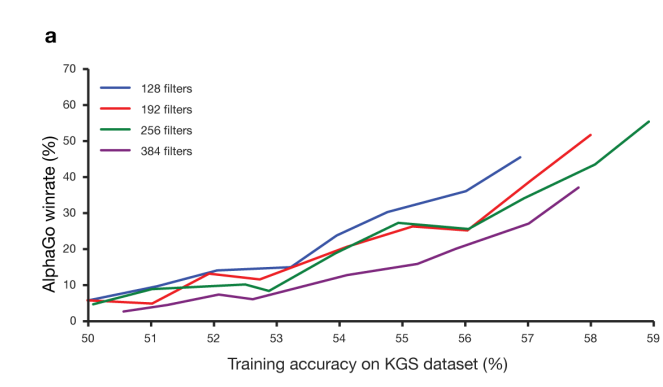
이때 network가 너무 크면 MCTS로 혼자 둬보는 상황에서 시간이 너무 많이 걸리기 때문에 rollout policy로 작은 network 도 따로 학습을 진행하였다.
이떄 rollout policy는 24.2%의 정확도를 달성
원본 supervised policy의 예측 시간은 3ms 이고 rollout의 경우 2 s의 시간이 소모(약 1500배 차이)
Reinforcement Learning of Policy Networks
rl policy는 처음에 supervised policy와 동일한 weight로 초기화를 시키고 policy gradient 강화학습을 진행하는데 이때 현재 학습하는 policy 와 이전에 학습을 하고 정해둔 iteration의 policy 을 가지고 대결을 하며 진행
이렇게 자신과 자신을 대결하는 것이 아니라 이전 iteration의 policy를 가지고 학습을 진행하는 이유는 현재 policy에 overfitting이 되는 문제를 막기 위함.
즉 지금의 나를 이기는 것이 중점이 되면 점점 이상하게 학습이 진행되면서 이길 수 있기에 EMA와 같이 천천히 과거의 자신을 가지고 학습을 하는것.
과거의 나를 이길 수 있어야 점점 강해지고 있는 것이기 때문에.
reward의 경우 마지막을 제외하고 싹다 0으로 설정.
마지막은 이기면 1 지면 -1로 설정
학습은 예측되는 outcome을 식으로 stochastic gradient ascent로 진행(REINFORCE라고 생각하면 될 것 같다.)
RL policy가 SL policy랑 붙으면 RL이 80%의 승률을 기록했다고 한다.
Reinforcement Learning of Value Networks
마지막은 value를 학습하는 것. value는 다음과 같다.
양 player가 policy p를 따라서 계속 진행했을 때의 reward 예측 값이다.
모든 상황에서 정확한 예측을 할 수 있는 optimal policy를 아는 것이 제일 좋겠지만 사실 불가능하기 때문에 RL policy를 가지고 approximation을 진행
value network의 구조는 policy와 동일하지만 1개의 값만 output으로 만든다.
학습은 각 state, z(승패 여부) pair를 가지고 regression으로 MSE loss를 줄이며 진행
dataset에서 전체 gameset을 가지고 학습을 하면 돌 1개만 다르고 correlate되어 있고 target은 동일하게 때문에 overfitting이 되기 쉽다.
실제로 학습을 할때 그냥 단순하게 학습하면 게임의 결과를 예측하는 것이 아니라 기억을 하게 됨.
그렇기에 RL끼리 플레이를 진행해고 각 게임마다 1개씩의 state와 결과를 가져와서 학습을 진행
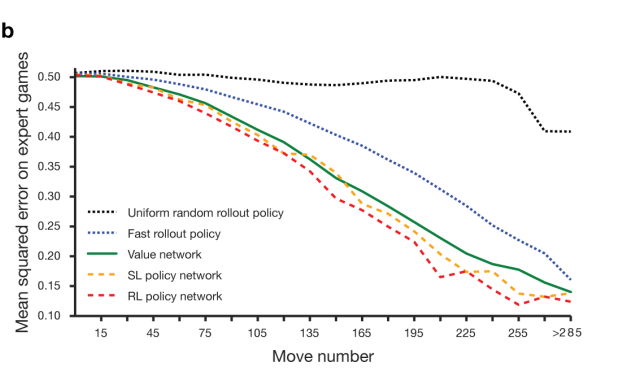 이렇게 구축한 value model을 이용하여 예측한 승패 MSE와 policy network를 직접 돌려서 예측하는 MSE를 보면 매우 비슷하다.
이렇게 구축한 value model을 이용하여 예측한 승패 MSE와 policy network를 직접 돌려서 예측하는 MSE를 보면 매우 비슷하다.
즉 value network로도 승패를 잘 예측할 수 있고 이는 직접 monte carlo로 돌려보는 것 대비 15000배나 빠르다.
Searching with Policy and Value Networks
앞서 우리는 supervised network, rollout network, RL network, value netwok 4개에 대한 이해를 마쳤다.
이들을 이용해서 MCTS 즉 몬테카를로 트리 서치를 진행하여 실제 게임을 진행하게 된다.
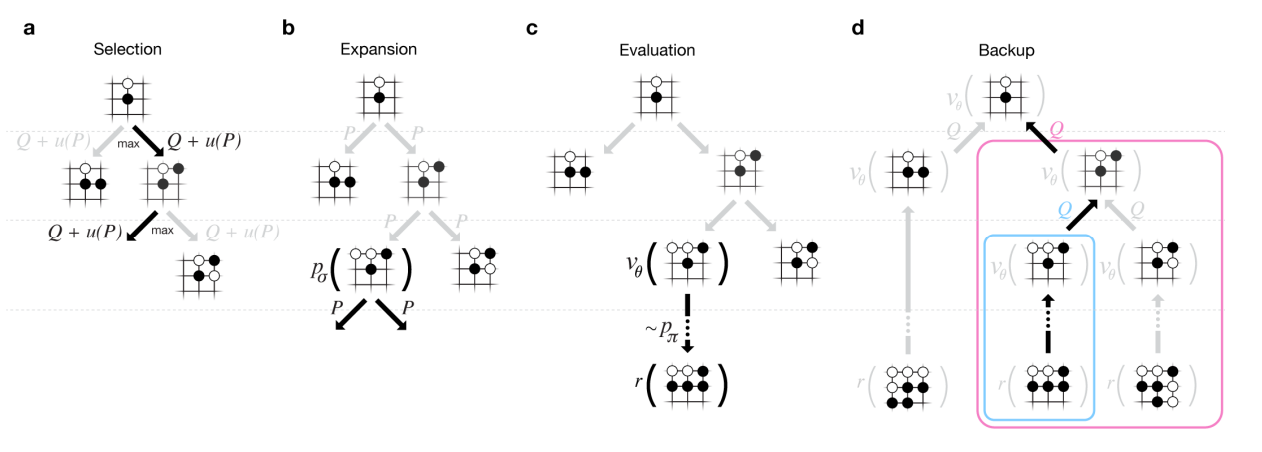
위처럼 진행되고 각 edge는 action value 와 visit count 그리고 prior priority 를 가진다. 이때 prior priority는 말그대로 사전분포. 그냥 아무것도 안했을 때의 SL policy의 확률이다.
selection
이를 토대로 root부터 시작해서 각 time step t에서 에서 를 고르는데
로 진행이 되며
이다.
위 수식의 의미는 학습 초반에는 현재 추정한 action value Q가 정확하지 않기에 u의 N이 낮게 되어 u에 더 의존을 해서 진행이 되고
학습 후반에는 action value Q가 더 정확하게 되기에 N이 높아져 u에 의존을 더 하지 않게 된다.
이를 토대로 action을 선택한다.
여기까지가 위 그림의 selection 단계이다.
Expansion
이렇게 action을 선택하면서 traversal을 계속 하다가 leaf node에 도달하게 되면 leaf node를 SL policy로 1 step 진행하는 식으로 expand해서 새로운 node 1개를 달고 이때 prior probability 로 저장해둔다.
Evaluation
그리고 이렇게 달린 node는 2가지 방법으로 평가가 되는데
- value network 를 통해 평가
- rollout policy로 끝가지 진행한 후 평가
위 두 결과를 비율합해서 로 진행
위 비율을 0.5로 두는 것이 가장 좋았다고 함.
Backup
다시 root로 돌아가면서 visit count와 action value를 update를 한다.
(s,a,i)는 i번째 edge가 방문되었는지 여부이고
은 i th simulation의 leaf node의 value이다.
그러니까 leaf에서 root로 돌아가면서 거쳐왔던 edge의 N은 1을 더해주고 Q에는 평균을 더 이동해준다.
이렇게 search를 진행하고 가장 많이 Visit된 곳으로 이동한다
가장 value가 높은 곳이 아니라 가장 visit이 많은 곳으로 가는 이유는
우리가 식당을 갈때 3명이 평가하고 5.0점인 곳과 500명이 평가하고 4.7점인 곳 중에서 후자가 더 실질적으로 안정되고 높은 결과를 보이기 때문이다.거기다가 Q와 p가 높은 곳으로 방문을 하기 때문에 점점 특정 value가 높은 action을 반복적으로 진행하기에 많이 방문한 곳이 제일 stable하고 실제로 높은 곳일 확률이 높기 때문이다.
왜 SL policy?
이때 한가지 의문이 들 수 있다.
MCTS를 진행할때 왜 더 강력한 RL policy대힌 SL policy를 쓰는 것일까?
실질적으로 RL은 value network를 학습할 때 말고는 사용되지 않는다.
왜냐하면 MCTS를 진행할 때 RL policy 대신 SL policy가 더 성능이 잘 나오기 때문이다.
그 이유는 사람은 여러 가지 경우의 수를 고려해서 진행을 하는데(실제로 SL policy의 정확도는 아무리 학습해도 50%)
그러나 RL policy는 지금 state에 최선의 수 1개를 생각하기에 1개의 수로 집중이 된다.
그렇기에 RL에서 중요한 exploration을 잘 못하게 되고 더 좋은 수가 있는데 발견을 잘 못하게 된다.
evaluation
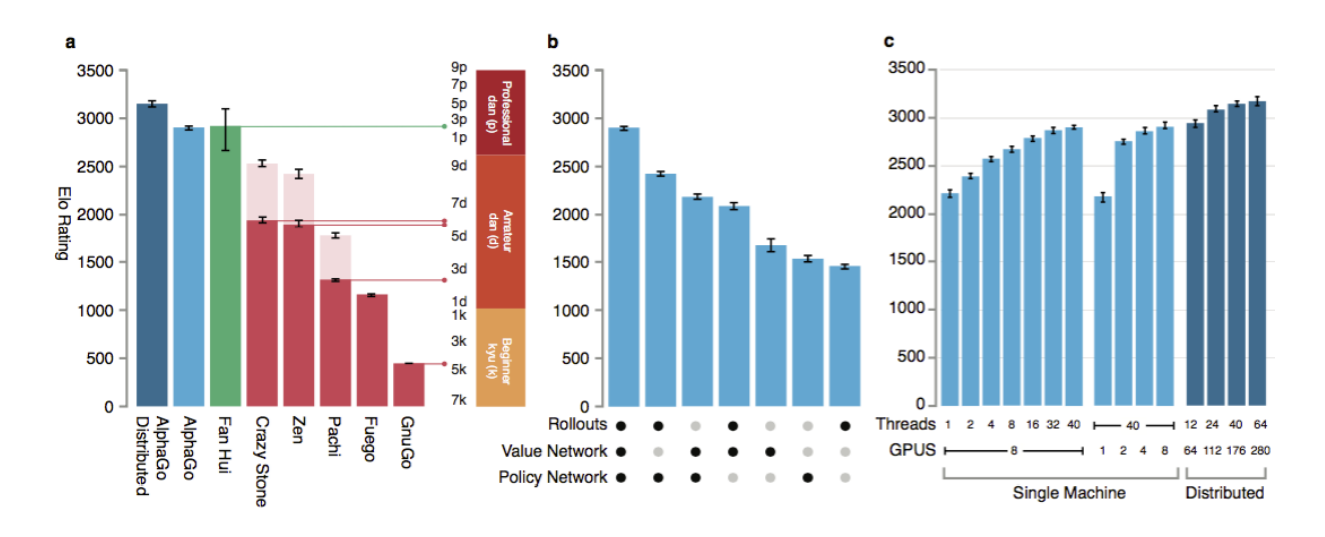
실제로 알파고는 이러한 과정을 통해 다른 바둑 프로그램들을 싹다 99.8%의 승률로 이긴 다음 이세돌 9단을 이기고 세계 최강자가 되었다.