[논문 리뷰]Simple and Effective Masked Diffusion Language Models

논문링크

지난번에 이어서 이번에도 세미나를 준비하며 notion에 작성한 다음 옮겼기에 글자가 이상할 수 있다.

요약

D3PM의 absorb Noise를 활용한 Text 생성에서 assumption을 추가해서 Rao-Blackwellized를 활용한 objective를 만들었다.

추가로 continuous time diffusion, DiT 등 다양한 기술을 추가하였고

기존 diffusion 기반 text 생성 모델을 outperform하는 성능을 얻었음

1 Introduction

diffusion model은 autoregressive와 다르게 한번에 생성하기 때문에 long-term planning, controllable generation, sampling speed에서 뛰어나다.

하지만 discrete diffusion은 AR에 비해서 성능이 떨어진다.

이 논문은 Masked Diffusion Language Model(MDLM)을 제시함. 이전의 D3PM의 text generation을 개선한 것으로 생각하면 된다.

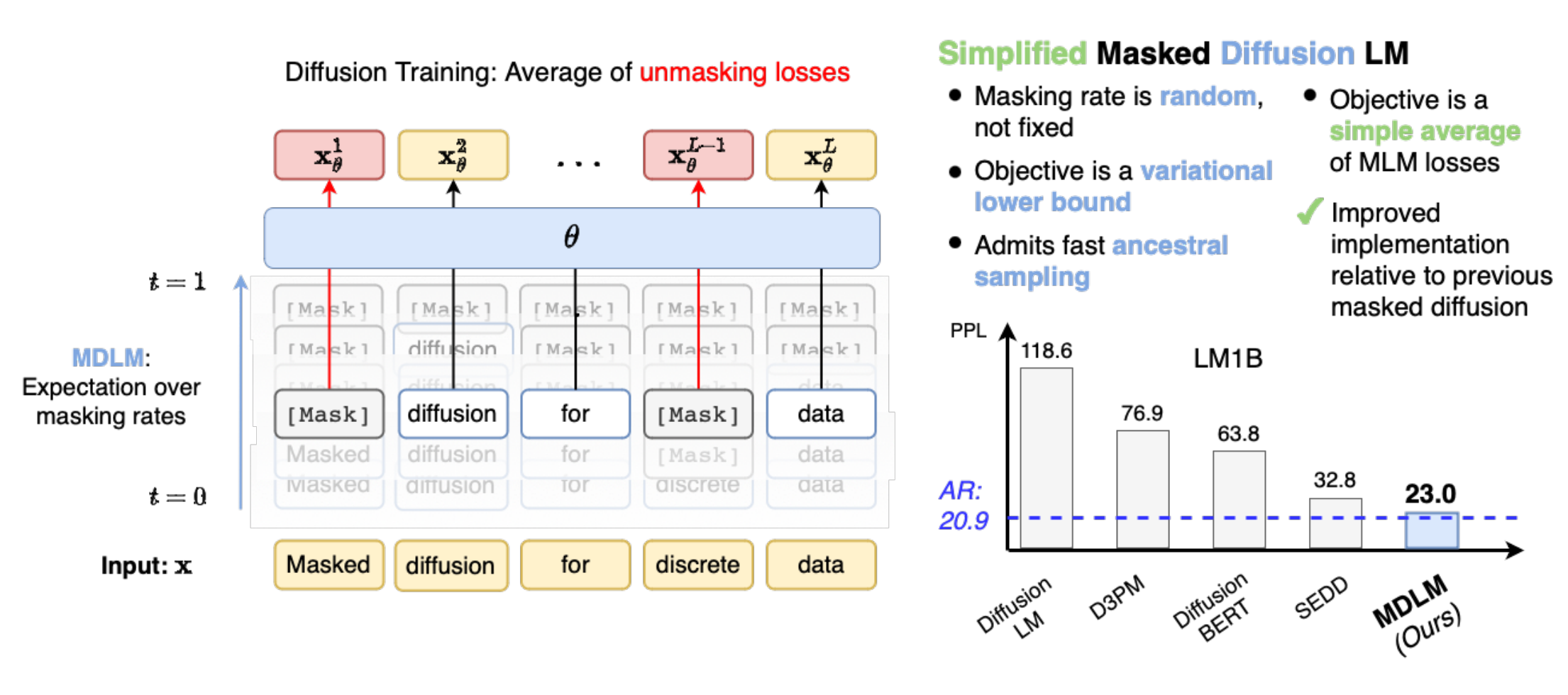
위처럼 구성

reverse diffusion process를 Rao-Blackwellized continuous-time variational lower bound로 더욱 tight하게 만들었다.

Background

diffusion에 대한 내용이다.

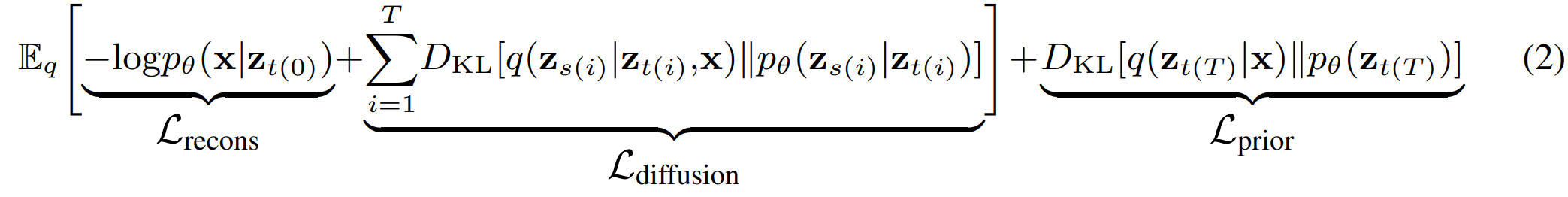
위 내용은 Negative ELBO(NELBO)이다.

아래 내용은 Discrete Diffusion에 대한 내용인데

$q(z_t|x)=\text{Cat}(z_t;\bar Q_tx)=\text{Cat}(z_t;Q_tQ_{t-1}...Q_1x)$로 이전에 D3PM의 $\bar Q_t=Q_1Q_2...Q_t$와는 반대 방향으로 표기가 되어있다…

3 Simple Masked Diffusion Models

이전 D3PM에서 absorbing state가 뛰어난 성능을 보였는데 이를 Rao-Blackwellized objective로 수정해서 더 좋게 바꿨다고 하는데 앞에 대한 이해가 필요하기에 한번 천천히 보자.

• Notation: $\pi$(prior vector, uniform, absorb 등…)

3.1 Interpolating Discrete Diffusion

이 논문에서는 continuous time에 대해서도 다뤄야 하기 때문에 특이하게 Q를 설정한다

여기에서 다 설정하고 가겠다.

$s<t$에서

$Q_{t|s}=\alpha_{t|s}\mathbf I+ (1-\alpha_{t|s}\mathbf 1 \mathbf{\pi}^\top)$이라고 하면

$q(\mathbf{z}_t \mid \mathbf{z}_s) = \text{Cat}(\mathbf{z}_t; Q^\top_{t \mid s} \mathbf{z}_s) \\ = \text{Cat}(\mathbf{z}_t; [\alpha_{t \mid s} \mathbf{I} + (1 - \alpha_{t \mid s}) \mathbf{1} \boldsymbol{\pi}^\top]^\top \mathbf{z}_s) \\ = \text{Cat}(\mathbf{z}_t; \alpha_{t \mid s} \mathbf{z}_s + (1 - \alpha_{t \mid s}) \boldsymbol{\pi} \mathbf{1}^\top \mathbf{z}_s) \\ = \text{Cat}(\mathbf{z}_t; \alpha_{t \mid s} \mathbf{z}_s + (1 - \alpha_{t \mid s}) \boldsymbol{\pi}).$

이다. 중간에 $1^\top \mathbf z_s=1$이다.

여기에서 논문에 처음 $z_t=Q_tz_{t-1}$이라고 해놓고 왜 $Q^\top$을 넣는지는 모르겠다 오타인가?
뒤에서는 $Q^\top$을 기준으로 계속 진행된다.

$q(\mathbf{z}_s \mid \mathbf{z}_t, \mathbf{x}) = \text{Cat}\left(\mathbf{z}_s; \frac{(Q_{t \mid s} \mathbf{z}_t) \odot (Q_s^\top \mathbf{x})}{\mathbf{z}_t^\top Q_t^\top \mathbf{x}}\right)$인데 이것은 D3PM 논문에 유도과정이 나와있었다.

유도
이 논문은 D3PM이랑 표기가 달라서 다시 유도해보자면
$q(\mathbf z_s|\mathbf z_t, \mathbf x)=\frac{q(\mathbf z_t|\mathbf z_s, \mathbf x)q(\mathbf z_s|\mathbf x)}{q(\mathbf z_t|\mathbf x)}=\frac{q(\mathbf z_t|\mathbf z_s)q(\mathbf z_s|\mathbf x)}{q(\mathbf z_t|\mathbf x)}= \frac{Q_{t|s}\mathbf z_t\odot Q^\top_s \mathbf x}{\mathbf z^\top_t Q^\top_t \mathbf x}$이다.

이를 처음 식으로 풀어서 적으면

$q(\mathbf{z}_s \mid \mathbf{z}_t, \mathbf{x}) = \text{Cat}\left(\mathbf{z}_s; \frac{[\alpha_{t \mid s} \mathbf{I} + (1 - \alpha_{t \mid s}) \mathbf{1} \boldsymbol{\pi}^\top] \mathbf{z}_t \odot [\alpha_s \mathbf{I} + (1 - \alpha_s) \mathbf{1} \boldsymbol{\pi}^\top]^\top \mathbf{x}}{\mathbf{z}_t^\top [\alpha_t \mathbf{I} + (1 - \alpha_t) \mathbf{1} \boldsymbol{\pi}^\top]^\top \mathbf{x}}\right) \\= \text{Cat}\left(\mathbf{z}_s; \frac{[\alpha_{t \mid s} \mathbf{z}_t + (1 - \alpha_{t \mid s}) \mathbf 1 \boldsymbol{\pi}^\top \mathbf{z}_t] \odot [\alpha_s \mathbf{x} + (1 - \alpha_s) \boldsymbol{\pi}]}{\mathbf{z}_t^\top [\alpha_t \mathbf{x} + (1 - \alpha_t) \boldsymbol{\pi} \mathbf 1^\top \mathbf x]}\right) \\= \text{Cat}\left(\mathbf{z}_s; \frac{[\alpha_{t \mid s} \mathbf{z}_t + (1 - \alpha_{t \mid s}) \mathbf 1 \boldsymbol{\pi}^\top \mathbf{z}_t] \odot [\alpha_s \mathbf{x} + (1 - \alpha_s) \boldsymbol{\pi}]}{\alpha_t \mathbf{z}_t^\top \mathbf{x} + (1 - \alpha_t) \mathbf{z}_t^\top \boldsymbol{\pi}}\right).$

이다.

$p_\theta(\mathbf{z}_s \mid \mathbf{z}_t) = q(\mathbf{z}_s \mid \mathbf{z}_t, \mathbf{x} = \mathbf{x}_\theta(\mathbf{z}_t, t)) \\ = \text{Cat}\left(\mathbf{z}_s; \frac{(Q_{t \mid s} \mathbf{z}_t) \odot (Q_s^\top \mathbf{x}_\theta(\mathbf{z}_t, t))}{\mathbf{z}_t^\top Q_t^\top \mathbf{x}_\theta(\mathbf{z}_t, t)} \right).$
이다. 간단하게 위 식에서 $\mathbf x_\theta(\mathbf z_t,t)$로 $\mathbf x$를 모델링 한 것이다.

3.2 Masked Diffusion

Absorb Noise에 따라서 masking된 diffusion에 대한 설명

3.2.1 Forward Masking Process

absorb stete등의 masked diffusion에서 $\boldsymbol \pi= \mathbf m$이다.

여기에서 reverse를 진행할 때 다음과 같은 분포를 따르게 되는데

$q(\mathbf{z}_s \mid \mathbf{z}_t, \mathbf{x}) = \begin{cases} \text{Cat}(\mathbf{z}_s; \mathbf{z}_t) & \text{if } \mathbf{z}_t \neq \mathbf{m}, \\ \text{Cat}\left(\mathbf{z}_s; \frac{(1 - \alpha_s)\mathbf{m} + (\alpha_s - \alpha_t)\mathbf{x}}{1 - \alpha_t}\right) & \text{if } \mathbf{z}_t = \mathbf{m}.\end{cases}$

의미는 $\mathbf z_t$가 maked token이 아니면 그냥 그대로 진행하고 만약 masked token이면 $\frac{1-\alpha_s}{1-\alpha_t}$의 확률로 masking되고 $\frac{\alpha_s-\alpha_t}{1-\alpha_t}$의 확률로 원본을 복구한다.

왜 그렇냐면

$q(\mathbf z_s|\mathbf z_t,\mathbf x)=\text{Cat}\left(\mathbf{z}_s; \frac{[\alpha_{t \mid s} \mathbf{z}_t + (1 - \alpha_{t \mid s}) \mathbf 1 \boldsymbol{\pi}^\top \mathbf{z}_t] \odot [\alpha_s \mathbf{x} + (1 - \alpha_s) \boldsymbol{\pi}]}{\alpha_t \mathbf{z}_t^\top \mathbf{x} + (1 - \alpha_t) \mathbf{z}_t^\top \boldsymbol{\pi}}\right).$에서

• case 1) $\mathbf z_t=\mathbf x$인 경우 위식에 대입하면
  $\mathbf{x^\top m=}0$이기 때문에
  $\text{Cat}\left(\mathbf{z}_s; \frac{[\alpha_{t \mid s} \mathbf{x} + (1 - \alpha_{t \mid s}) \mathbf 1 \mathbf{m}^\top \mathbf{x}] \odot [\alpha_s \mathbf{x} + (1 - \alpha_s) \mathbf{m}]}{\alpha_t \mathbf{x}^\top \mathbf{x} + (1 - \alpha_t) \mathbf{x}^\top \mathbf{m}}\right)=\text{Cat}(\mathbf{z}_s;\frac{[\alpha_{t|s}\mathbf x]\odot[\alpha_s\mathbf x+(1-\alpha_s)\mathbf m]}{\alpha_t})=\text{Cat}(\mathbf{z}_s; \frac{\alpha_t\mathbf x}{\alpha_t})=\text{Cat}(\mathbf{z}_s; \mathbf x)$가 된다.

• case2) $\mathbf z_t=\mathbf m$인 경우
  $q(\mathbf{z}_s \mid \mathbf{z}_t = \mathbf{m}, \mathbf{x}) = \text{Cat}\left( \frac{\left( \alpha_{t \mid s} \mathbf{m} + (1 - \alpha_{t \mid s}) \mathbf{1} \right) \odot \left( \alpha_s \mathbf{x} + (1 - \alpha_s) \mathbf{m} \right)}{1 - \alpha_t} \right) \\= \text{Cat}\left( \frac{\alpha_{t \mid s} (1 - \alpha_s) \mathbf{m} + (1 - \alpha_{t \mid s})(1 - \alpha_s) \mathbf{m} + (\alpha_s - \alpha_t) \mathbf{x}}{1 - \alpha_t} \right)\\=\text{Cat}(\mathbf z_s;\frac{(1-\alpha_s)\mathbf m+(\alpha_s-\alpha_t)\mathbf x}{1-\alpha_T})$
  를 만족하고
  여기에서
  $q(\mathbf z_s=\mathbf x|\mathbf{z_t=m,x})=\frac{\alpha_s-\alpha_t}{1-\alpha_t}$
  $q(\mathbf z_s=\mathbf m|\mathbf{z_t=m,x})=\frac{1-\alpha_s}{1-\alpha_t}$를 보인다.

3.2.2 Reverse Unmasking Process

생성은 Noise로부터 복구하는 것인데 $p_\theta(\mathbf z_s|\mathbf z_t)$로 $q(\mathbf z_s|\mathbf z_t,\mathbf x)$를 근사해서 진행하게 되는데 $q(\mathbf z_s|\mathbf z_t,\mathbf x)$가 $\mathbf x$에 condition이 되어있는데 우리가 $\mathbf x$를 잘 모르니까 $\mathbf x_\theta(\mathbf z_t,t)$를 근사해서 network를 만들었고 이를 이용해서 posterior를 추정하는 것이다.

여기에서 만약 time에 대한 dependency t를 제외하면 inference speed를 2배 더 빠르게 할 수 있다는 이야기

3.2.3 SUBS Parameterization
위에서 말한 것처럼 x를 추정해서 parameterization 진행하면

$p_\theta(\mathbf{z}_s \mid \mathbf{z}_t) = q(\mathbf{z}_s \mid \mathbf{z}_t, \mathbf{x} = \mathbf{x}_\theta(\mathbf{z}_t, t)) = \begin{cases} \text{Cat}(\mathbf{z}_s; \mathbf{z}_t), & \mathbf{z}_t \neq \mathbf{m}, \\ \text{Cat}\left(\mathbf{z}_s; \frac{(1 - \alpha_s) \mathbf{m} + (\alpha_s - \alpha_t) \mathbf{x}_\theta(\mathbf{z}_t, t)}{1 - \alpha_t} \right), & \mathbf{z}_t = \mathbf{m}.\end{cases}$

위와 같이 나오게 되는데

여기에서 중요한 2가지 추정을 추가할 수 있다.

간단하다

1. Zero Masking Probabilities: $\langle \mathbf x,\mathbf m \rangle=0$이다. 그렇기에 $\langle \mathbf x_\theta(\mathbf z_t,t), \mathbf m\rangle=0$이라고 넣어주는 것.
2. Carry-Over Unmasking: 이미 한번 unmaked된 것은 carry over 즉 계속 가져간다. network의 output을 바꾸지 않고 가져간다.

3.3 Rao-Blackwellized Likelihood Bounds

위 2가지 가설을 바탕으로 모델을 더 분산을 줄이면서 학습을 할 수있는데 이는 Rao-Balckwellized와 비슷하다.

• Rao-Balckwellized란? 나도 대략적으로 읽고 넘어갔는데 어떤 확률 $\theta$에 대한 추정량 $S(X)$가 있을 때 충분통계량 $T(X)$가 주어지면 $\mathbb E[S(X)|T(X)]=\mathbb E[S(X)]$이고 $\text{Var}[S(X)|T(X)]<\text{Var}[S(X)]$이다.
  

간단하게 위의 경우 Zero Masking Probability, Carry-over unmasking 등의 조건을 더 붙임으로 써

모델이 $\mathbf m=0$을 학습해야 하는 부담을 덜어주고 더 정확한 값의 표현이 가능해진 것

결국 KL divergence를

$\mathcal{L}_{\text{diffusion}} = \sum_{i=1}^T \mathbb{E}_q \left[ D_{\text{KL}} \left( q(\mathbf{z}_s(i) \mid \mathbf{z}_t(i), \mathbf{x}) \parallel p_\theta(\mathbf{z}_s(i)) \right) \right] \\= \sum_{i=1}^T \mathbb{E}_q \left[ \frac{\alpha_t(i) - \alpha_s(i)}{1 - \alpha_t(i)} \log \left\langle \mathbf{x}_\theta(\mathbf{z}_t(i)), \mathbf{x} \right\rangle \right]$

이렇게 표현이 가능하고 더욱 안정적인 결과를 얻을 수 있었다고 한다.

유도 과정은 논문 appendix B.1.3에 있다.

3.4 Continuous-Time Likelihood Bounds

앞에서 D3PM의 경우 우리는 time이 discrete하다고 가정하고 진행을 하였는데

$T\rightarrow \infin$인 경우 ELBO를 더욱 tight하게 구성할 수 있다.

간단하게 위 수식에서 유도하자면

$\lim_{T\rightarrow\infin}\sum_{i=1}^T \mathbb{E}_q \left[ \frac{\alpha_t(i) - \alpha_s(i)}{1 - \alpha_t(i)} \log \left\langle \mathbf{x}_\theta(\mathbf{z}_t(i)), \mathbf{x} \right\rangle \right]=\mathbb{E}_q \left[\lim_{T\rightarrow\infin}\sum^T_{i=1} \frac{\alpha_t(i) - \alpha_s(i)}{1 - \alpha_t(i)} \log \left\langle \mathbf{x}_\theta(\mathbf{z}_t(i)), \mathbf{x} \right\rangle \right]=\mathbb{E}_q \left[\lim_{T\rightarrow\infin}\sum^T_{i=1} \frac{\alpha_t(i) - \alpha_s(i)}{1 - \alpha_t(i)} \log \left\langle \mathbf{x}_\theta(\mathbf{z}_t(i)), \mathbf{x} \right\rangle \frac{1}{T}*T\right]=\mathbb E_q \int^{t=1}_{t=0}\frac{\alpha'_t}{1-\alpha_t}\log \left\langle \mathbf{x}_\theta(\mathbf{z}_t,t), \mathbf{x} \right\rangle dt$

인데 $\lim_{T\rightarrow\infin}T(\alpha_t(i)-\alpha_s(i))=\alpha_t'$인 이유는 $\Delta t=\frac{1}{T}$라고 할때 $\alpha_s(t)=\alpha_t(t-\Delta t)$로 표현이 가능하다.

그리고 $\lim_{T\rightarrow\infin}\Delta t=0$이니까 $\lim_{\Delta t\rightarrow0}\frac{\alpha_t(t)-\alpha_t(t-\Delta t)}{\Delta t}=\alpha_t'(t)$를 만족한다.

이렇게 continuous로 유도가 되면 Noise Schedule에 Invariance하다는데 이 부분은 잘 와닿지 않고 중요한 부분은 아니니 제외하겠다.

3.5 Masked Diffusion Language Models

결국 위와 같이 구해서 이전 sequence 전부를 받고 1글자씩 독립적으로 예측이 되는 모델이 있을 때

NELBO는 다음과 같이 유도가 된다.

$\mathcal{L}^{\infty}_{\text{NELBO}} = \mathbb{E}_q \int_{t=0}^{t=1} \frac{\alpha_t'}{1 - \alpha_t} \sum_{\ell} \log \left\langle \mathbf{x}_\theta^\ell (\mathbf{z}_t^{1:L}, t), \mathbf{x}^\ell \right\rangle dt$

재밌는건 이렇게 구성된 objective가 MLM loss와 똑같은 모양이다.

정확히는 weighted average of MLM loss

3.5.1 Training Considerations for Masked Diffusion

학습을 위해서 추가한 내용에 대해서 설명을 하는데

tokenizer가 상당한 영향을 주었다는데 vocabulary의 size가 작으면 단어를 더 잘게 나눠서 표현을 해야하기 때문에 sequence가 길어지고 long term dependency 문제가 발생한다.

model은 D3PM은 T5을 사용하였는데 발전된 DiT를 넣었고

sample도 랜덤이 아니라 low-discrepancy sampler를 사용하였다고 한다.

4 Inference and Sampling in Masked Diffusion Language Models

4.1 Efficient Ancestral Sampling

전체가 masked token에서 시작해서 점점 step을 밟으면서 제거해나가는 것이다.

만약 이전 step에서 denoising이 된 token이 없어 다음 step과 동일하다면 $\mathbf x_\theta(\mathbf z^{1:L}_t)$처럼 시간에 independent한 모델을 사용할 때 그 output을 cache를 하고 이전에 미리 계산된 값을 다시 사용해서 진행할 수 있다.

4.2 Semi-Autoregressive Masked Diffusion Language Models

처음 $\tilde{\mathbf x}^{1:L}$을 생성하고 $L'$만큼 뒤에 추가로 생성하고 싶다면

앞에서 생성한 token $\tilde{\mathbf x}^{L-L':L}$을 prefix로 달고 $\mathbf z^l_s\sim p_\theta(\mathbf z_s^l |\mathbf z_t^{L:L+L'})$의 생성을 진행한다.

이를 계속 반복하면 autoregressive하게 생성이 가능하다.