[논문 리뷰 및 구현]Identity Mappings in Deep Residual Networks

논문 주소

1. Introduction

• 이전논문 Deep Residual Learning for Image Recognition
  에서 사용된 residual block은 다음과 같이 수식으로 표현할 수 있다.
  
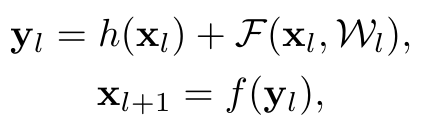
  여기에서 Xl은 l번째 input이고 Xl+1은 l+1번째 input이다. F는 residual function이고 h(xl)=xl은 skip connection에서 identity mapping을 의미한다.
  그리고 f는 relu 함수였다.

• 이전에 h(xl)=x인 identity mapping을 유지하는 skip connection에 대해서 F(x)를 학습하는 방법을 통해서 엄청나게 깊은 layer를 가진 모델은 만들 수 있었는데 이 논문에서는 전체 네트워크를 지나는 "information direct path"의 중요성에 대해서 다룬다.

• 만약 위 수식에서 f와 h가 identity mapping이라면 forward, backward 정보는 다른 레이어로 바로 전달될 수 있다. 이러한 direct connection이 학습을 어떻게 더 쉽게 만드는지를 다룬다.

• 또한 논문에서는 기존의 post-activation과는 다르게 pre-activation을 이용해서 direct path를 잘 활용할 수 있게 clean한 information이 전달될 수 있게 만든다.

2. Analysis of Deep Residual Networks

• 기존의 residual network는 똑같은 residual block을 쌓아서 만드는데 블럭 하나하나를 residual unit이라고 하고 수식은 다음과 같다.
  
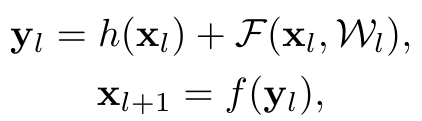
  l번째 residual unit의 output이 l+1번째 residual unit의 input으로 들어가는 것을 의미하는 수식이다. F는 residual function을 의미한다.

• 만약 f가 identity mapping이라면 xl+1=yl이 되고 다음 수식을 만족한다.
  
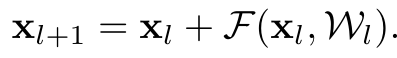
  이를 통해 재귀적으로 더하여 layer를 여러개 중첩한 것을 표현할 수 있는데 다음과 같다.
  
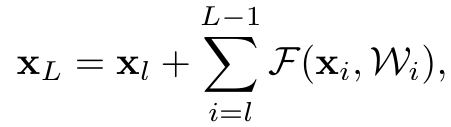
  이는 l번째 유닛부터 진행이 되어서 L번째 유닛에 들어가는 input을 의미한다. 여기에서 2가지 사실을 알 수 있다.

  1. layer L이 얼마나 깊든지 xL의 값은 얕은 xl의 값 + layer들의 residual function 합으로 표현이 가능하다다.
  2. $\mathbf{x}_L=\mathbf{x}_0+\sum_{i=0}^{L-1}(F(x,Wi))$로 표현이 가능한데 이는 곱셈으로 연산이 되는 plain network와 다르다. plain network는 곱셈이기에 $\prod_{i=0}^{i=L-1}\mathbf{W}_i\mathbf{x}_0$로 표현이 된다.

• 또한 sigma로 표현한 위 식은 back propagation에서도 이점을 보인다.
  
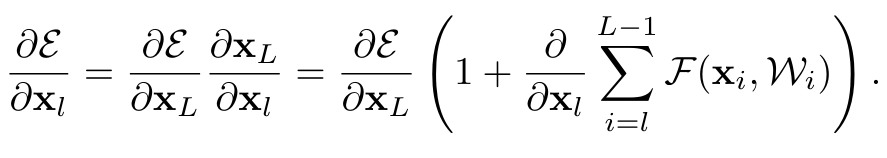
  loss function $\mathcal{E}$를 l번째 x로 미분을 하게 된다면 위와 같이 표현이 가능하고 여기에서 epsilon을 $\mathbf{x}_L$로 미분한 값은 loss function에서 어떤 layer든지 $\mathbf{x}_L$로 direct information propagation이 가능함을 의미하고 뒤의 $\left( 1 + \frac{\partial}{\partial \mathbf{x}_l} \sum_{i=l}^{L-1} \mathcal{F}(\mathbf{x}_i, \mathbf{W}_i) \right)$ 연산 부분은 그 사이 여러 layer를 거치는 것을 의미한다.
  그리고 $\left(\frac{\partial}{\partial \mathbf{x}_l} \sum_{i=l}^{L-1} \mathcal{F}(\mathbf{x}_i, \mathbf{W}_i) \right)$ 부분은 보통 모든 minibatch에서 -1이 되지는 않기 때문에 gradient의 vanish문제도 해결할 수 있다.

3. On the Importance of Identity Skip Connections

• 이 부분에서는 기존 함수에서 f를 identity mapping으로 유지하고 $\mathbf{X}_{l+1}={h}(\mathbf{X}_{l})+F(\mathbf{X}_{l},\mathbf{W}_{l})$에서 h함수를 중점으로 실험을 하였다.

1. $h\left(\mathbf{x}_{l}\right)=\lambda_{l} \mathbf{x}_{l}$으로 h함수를 곱셈 연산으로 치환하였다.
   $\mathbf{x}_{l+1}=\lambda_{l} \mathbf{x}_{l}+\mathcal{F}\left(\mathbf{x}_{l}, \mathcal{W}_{l}\right)$
   이 함수를 이전과 같이 재귀적으로 변환하면 다음과 같다.
   $\mathbf{x}_{L}=\left(\prod_{i=l}^{L-1} \lambda_{i}\right) \mathbf{x}_{l}+\sum_{i=l}^{L-1} \hat{\mathcal{F}}\left(\mathbf{x}_{i}, \mathcal{W}_{i}\right)$
   여기에서 $\hat{\mathcal{F}}$는 $\left(\prod_{j=i+1}^{L-1} \lambda_{j}\right) \mathcal{F}$를 의미한다.
   이제 똑같이 loss function에대해 미분하면 다음과 같다.
   $\frac{\partial \mathcal{E}}{\partial \mathbf{x}_{l}}=\frac{\partial \mathcal{E}}{\partial \mathbf{x}_{L}}\left(\left(\prod_{i=l}^{L-1} \lambda_{i}\right)+\frac{\partial}{\partial \mathbf{x}_{l}} \sum_{i=l}^{L-1} \hat{\mathcal{F}}\left(\mathbf{x}_{i}, \mathcal{W}_{i}\right)\right)$
   여기에서 알 수 있는 사실은 1이 $\prod_{i=l}^{L-1} \lambda_{i}$으로 치환이 됨으로써 곱셈 연산이 매우 많아지게 되었다. 결국 back propagation 과정에서 gradient vanishing이나 exploding이 발생할 수 있다는 것이다. 결국 shortcut 대신 weight layer에 의존을 하게 만든다.

• 이와 비슷하게 다른 1x1 conv, gating 등의 함수도 테스트가 되었는데 결국 propagation 과정에서 복잡하게 진행이 되기 때문에 identity mapping이 가장 정보전달에 있어서 안정적이다.

3.1 Experiments on Skip Connections

• 여기에서는 f를 identity mapping이 아닌 ReLU로 두고 다양한 테스트를 진행.
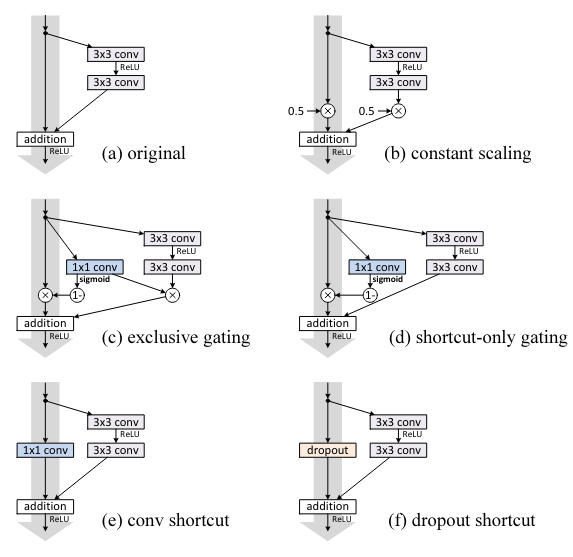
  그리고 아래는 그 결과이다.
  
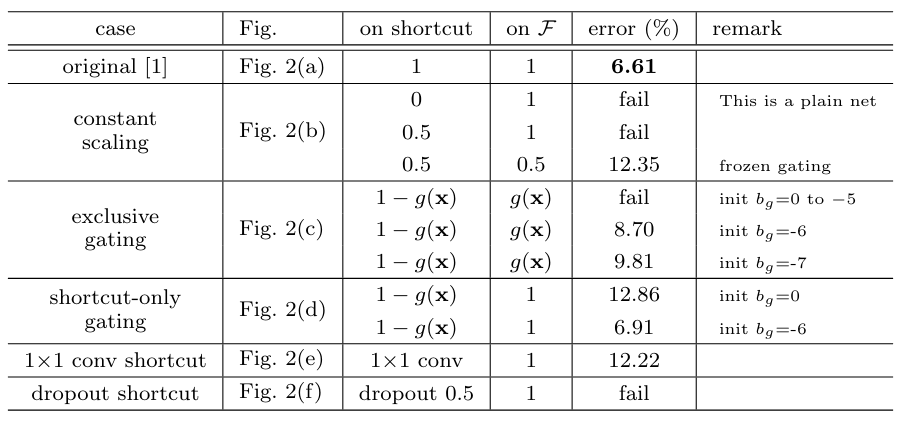
  fail은 20% 보다 error이 높으면 fail로 표기
  결국 original이 가장 좋았다.
  각각 이유를 작성하자면 다음과 같다.

1. constatnt scaling
   처음 언급했던 곱셈 모델 그러나 실제 구현에서는 $\lambda$를 두었는데 이는 skip connection에 곱해지는 값이고 $F$에서는 2가지 선택이 주어졌는데 $1-\lambda$가 곱해지거나 아니거나 이다. 곱해지지 않은 부분은 fail이 되었고 곱해진 부분은 12.35%로 original 보다 안좋은 결과를 내었다.
   그 원인은 이전에서 언급했듯이 back propagation에서의 방해로 보인다.
2. Exclusive gating
   이는 highway network를 따른 모양인데 $g(\mathbf{x})=\sigma\left(\mathrm{W}_{g} \mathbf{x}+b_{g}\right)$이런 구조로 구현이 되는데 $\sigma$는 sigmoid 함수이다. 여기에서 함수 $g$는 1x1 conv layer로 구현이 되고 각각 $X$와 $F$에 곱해지게 되는데 $X$에는 $1-g(\mathbf{x})$로 곱해지고 $F$에는 $g(\mathbf{x})$가 곱해진다.
   이 과정에서 bias의 값에 따라서 결과가 많이 달라지는데 최적의 값도 결국 original보다 나쁘다.
   이는 만약 $1-g(\mathbf{x})$의 값이 1에 가까워 진다면 identity mapping에 근접해져서 information propagation에 도움이 되지만 0에 가까워진다면 $F$함수만 사용하기 때문이다.
3. Shortcut-only gating.
   그렇기 때문에 위에서 이야기한 gating에서 $F$ 함수를 제외하고 $X$의 출력에만 영향을 줄 수 있게 바꾸었다.
   이는 확실히 이전보다 훨씬 나은 결과를 보였지만 역시 original이 더욱 좋았다. 그리고 bias가 매우 작은 값이 되어서 $1-g(\mathbf{x})$의 값이 1에 가까워 질수록 더 좋은 값을 보여주는데 이는 identity mapping에 가까울수록 좋은 결과를 보여주는 것을 의미하기도 한다.
4. 1×1 convolutional shortcut.
   이전 논문에서 identity mapping 과정에서 테스트 하였던 방법이다. 적은 layer의 residual network에서는 성능의 향상이 존재했지만 layer의 수가 많아지면 오히려 identity mapping보다 성능이 떨어진다. conv layer가 information propagation을 막기 때문이다.
5. Dropout shortcut.
   마지막은 dropout ratio 0.5인데 이 역시 성능이 떨어진다. dropout 과정에서 정보의 손실이 일어나기 때문. dropout은 fail이 되어버렸다. dropout은 통계학적으로 constatnt scaling에서 $\lambda=0.5$로 한 것과 비슷하다고 한다.

• 결국 모든 테스트에서 information propagation에 조금이라도 영향을 주는 요소가 있다면 성능이 떨어지기에 identity mapping이 가장 좋다는 결과를 얻을 수 있었다.
  또한 1x1 convolution을 적용하는 과정에서 1x1 convolution은 이론상 identity mapping이 될 수 있다. 그렇기 때문에 identity mapping보다 표현이 더욱 다채롭다. 하지만 실제 성능은 identity mapping이 더 좋다. 이는 optimization에서 degradation 문제가 다시 발생한 것으로 identity mapping이 이를 더욱 잘 다룰 수 있다고 볼 수 있다.

4. On the Usage of Activation Functions

• 아마 이 부분이 이 논문에서 가장 중요한 부분이라고 생각한다. 앞서 우리는 identity mapping의 중요성을 배웠다. 그러나 가장 깨끗한 identity mapping을 이루기 위해서는 어떻게 해야할까?
  결국 direct information path에 activation function도 제외를 해야 한다. 이를 위해 논문에서는 pre-activation을 도입하였다.

4.1 Experiments on Activation

여러가지 activation 구조를 테스트 하였는데 모든 구조는 다음과 같다.

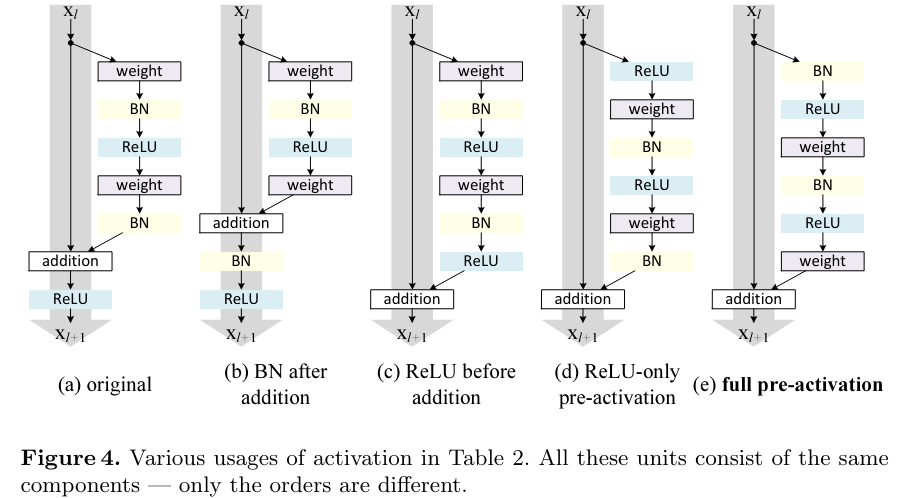
결과는 다음과 같다.

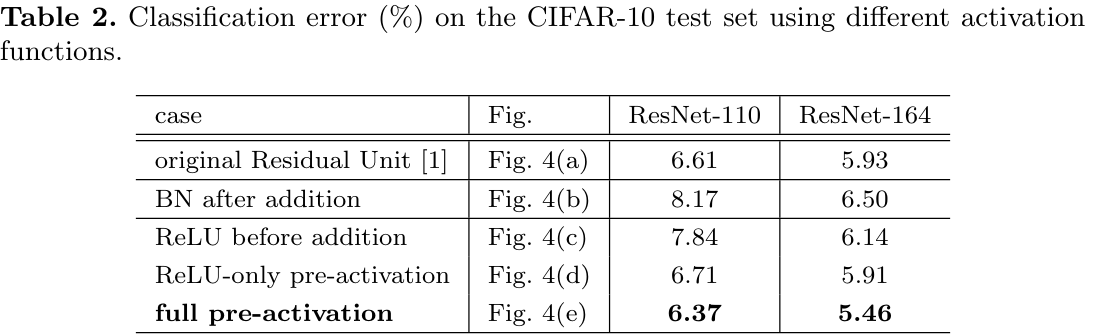
1. BN after addition
   이전과는 다르게 $X+F$를 진행한 후에 BN을 진행한다. 더 안좋은 결과를 보였다. BN의 information propagation을 방해하기 때문이다.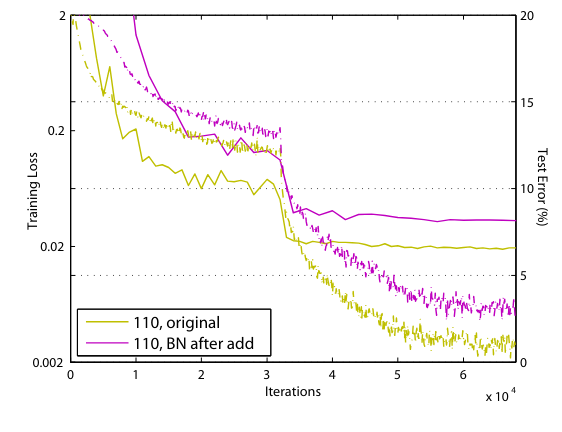
   실제 학습 결과를 보면 after BN이 loss가 적게 떨어진다.

2. ReLU before addition
   덧셈 연산 전에 residual unit 단계에서 ReLU까지 마치고 나오는 모습 이렇게 된다면 f는 오로지 identity mapping만 남게 되고 information의 direct 전달이 가능해진다. 하지만 $F$ 함수의 결과가 non-negative로 고정이 되기 때문에 main information path의 수정에 제한이 생기게 되어 main information은 계속 증가만 하기 때문에 representation 기능이 더 떨어져서 오히려 error이 더 증가하였다.

3. Post-activation or pre-activation?
   이전에 식에서 $\mathbf{x}_{l+1}=f\left(\mathbf{y}_{l}\right)$는 이제 다음 residual unit의 양쪽$X, F$ path 모두에 영향을 주었다. 그래서 asymmetric한 activation form을 개발해서 $X$부분은 영향을 주지 않고 $F$ 부분의 path만 영향을 주게 만들었다.
   다음과 같다.
   $\mathbf{x}_{l+1}=\mathbf{x}_{l}+\mathcal{F}\left(f\left(\mathbf{x}_{l}\right), \mathcal{W}_{l}\right)$결국 다음 F의 input 부분만 $f$를 적용하는 것이다.
   이 구조는 마치 pre-activation을 적용하는 것과 비슷하다
   그림으로 나타내면 다음과 같다.
   
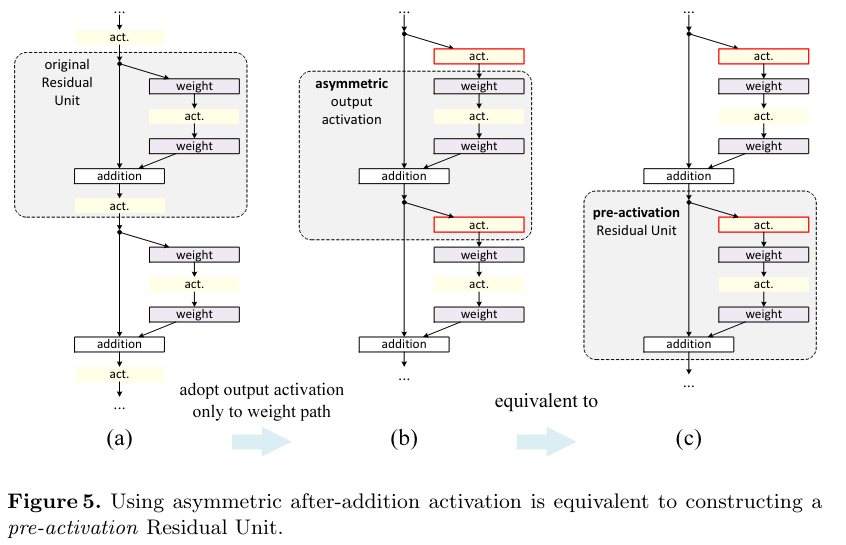
   (a)는 기존의 구조이고 (b)를 통해 F의 경로에만 $f$를 적용할 수 있고 (c)는 (b)의 형태를 좀 더 block화 한 것이다.
   또한 pre-activation에서도 ReLU only, full pre-activation 실험을 해보았는데 ReLU only에서는 ReLU layer가 BN과 연결되지 않아 BN의 이점을 얻지못해서 점수가 더 낮다.
   결국 full pre-activation이 가장 유의미한 결과를 내면서 좋은 구조임을 보여주었다.
   
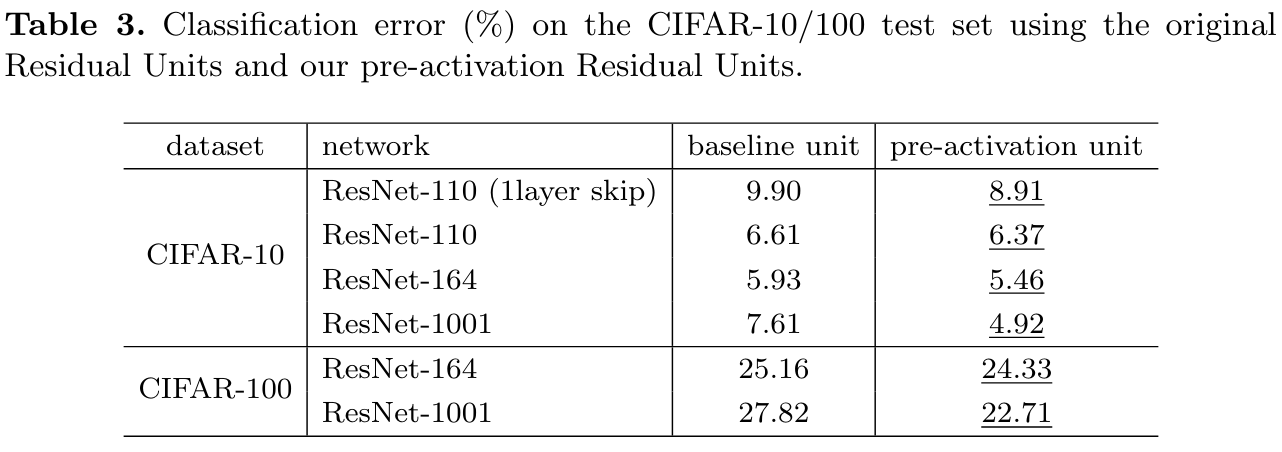
   모든 실험 결과에서 향상된 결과를 보여줌

4.2 Analysis

pre-activation의 2가지 이점이 있는데
1. optimization의 간단하게 만듦
2. BN을 pre-activation으로 넣으면 regularization을 추가해서 overfitting을 억제한 것과 비슷한 효과를 냄

Ease of optimization

1001 layer 모델의 학습 결과에서 보면 pre-activation 모델이 학습이 더 간단하다는 것을 알 수 있음

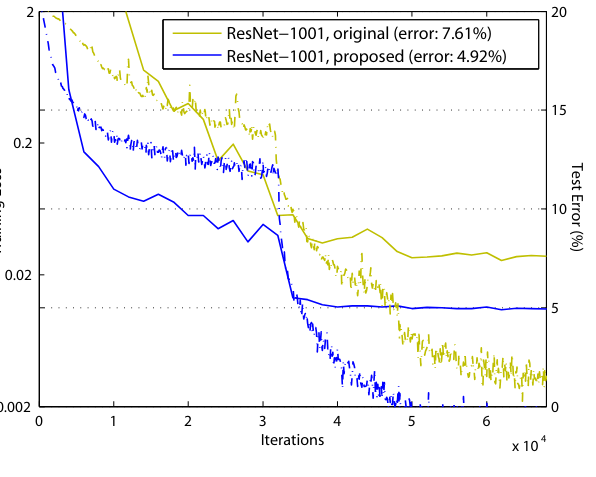
만약 f가 ReLU만 negative siganal이 영향을 받을 수 있고 많은 layer를 통과하면서 이 영향은 점점 쌓여서 커지게 된다.
또한 layer가 identity mapping이라면 propagation 과정에서 signal이 direct하게 전달이 가능해진다. 그래서 loss가 매우 빠르게 감소하는 모습을 보인다.

그런데 f=ReLU는 적인 layer에서는 영향이 크지 않다.

왜냐하면 training 과정에서 weight가 output을 양수로 가게 만들어서
ReLU 함수가 의미 없게 만들기 때문이다. 그러나 layer가 1001개 정도로 매우 많아지면 layer의 output이 음수로 가서 잘리는 경우가 많이 생기기 때문에 문제가 발생하는 것이다.

Reducing overfitting.

또 다른 이점으로는 overfitting이 억제되는 것이다.
바로 위의 이미지를 보면 164 layer 모델에서 pre-activation 모델은 training error이 normal model보다 더 높지만 test-error은 더 낮다.
이는 BN의 regularization 효과로 볼 수 있다.
original 모델은 BN이 적용되긴 하지만 shortcut과 합쳐지면서 BN의 효과가 사라지기 때문이다.
결국 unnormalized된 signal이 다음 layer에 들어가게 되고 BN의 효과를 볼 수 없게 된다.
그러나 pre-active가 된다면 모든 layer는 BN의 효과를 볼 수 있다.

Results

단지 preactive만 추가를 하였을 뿐인데 유의미한 성능 향상을 볼 수 있었다.
또한 더 깊은 model을 만들 수 있는 중요한 개념을 얻을 수 있었다.

appendix

논문 구현에서 first-layer과 last-layer에 신경을 썼는데 first-layer(single conv layer)와 last-layer(before avg pooling) 다음 extra activation을 추가해주었다.

code

32x32 cifar10 data를 학습하기 위해 만든 모델.
기존의 구현과는 조금 다르다.

class PreActResBlock(nn.Module):
    def __init__(self, in_channel, out_channel, is_downsample=False):
        super().__init__()
        stride = 2 if is_downsample else 1

        self.seq = nn.Sequential(
            nn.BatchNorm2d(in_channel),
            nn.ReLU(),
            nn.Conv2d(in_channel, out_channel, kernel_size=3,
                      stride=stride, padding=1, bias=False,),
            nn.BatchNorm2d(out_channel),
            nn.ReLU(),
            nn.Conv2d(out_channel, out_channel, kernel_size=3,
                      stride=1, padding=1, bias=False,),
        )
        if is_downsample:
            self.downsample = self._identitymap
        else:
            self.downsample = nn.Identity()

    def forward(self, x):
        return self.seq(x) + self.downsample(x)
        # identity map을 downsample하는 함수

    def _identitymap(self, x):
        x = x[:, :, ::2, ::2]
        y = torch.zeros_like(x)
        return torch.concat((x, y), dim=1)

class PreActResNet(nn.Sequential):
    def __init__(self, class_num=10):
        super().__init__(
            nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False),
            nn.ReLU(),
            PreActResBlock(64, 64),
            PreActResBlock(64, 64),
            PreActResBlock(64, 128, is_downsample=True),
            PreActResBlock(128, 128),
            PreActResBlock(128, 256, is_downsample=True),
            PreActResBlock(256, 256),
            PreActResBlock(256, 512, is_downsample=True),
            PreActResBlock(512, 512),
            nn.ReLU(),
            nn.AvgPool2d(4),
            nn.Flatten(),
            nn.Linear(512, class_num),
        )

실제 실험 결과

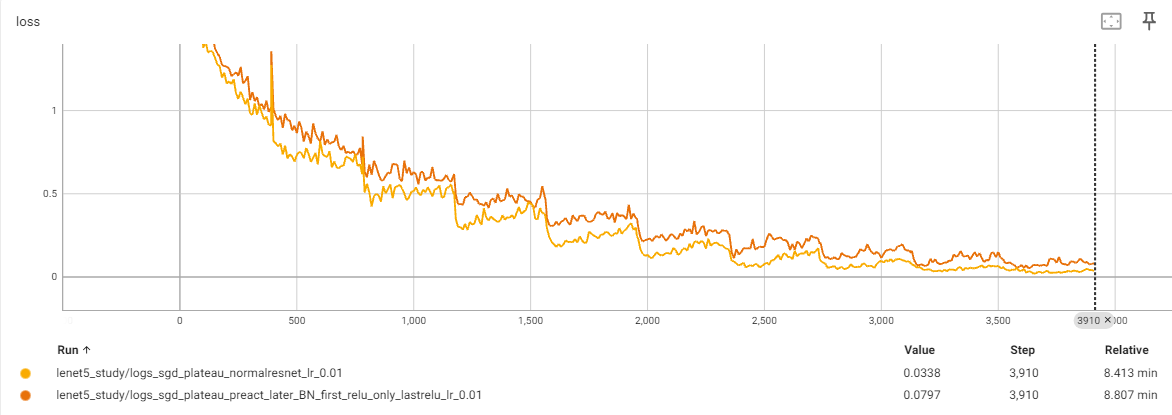
실제 preact를 적용할 시 논문에서 언급한 내용과 같이 초반에는 preact가 좋은 결과를 보여주지 않지만 후반으로 가면 좋은 결과를 보여주었다.

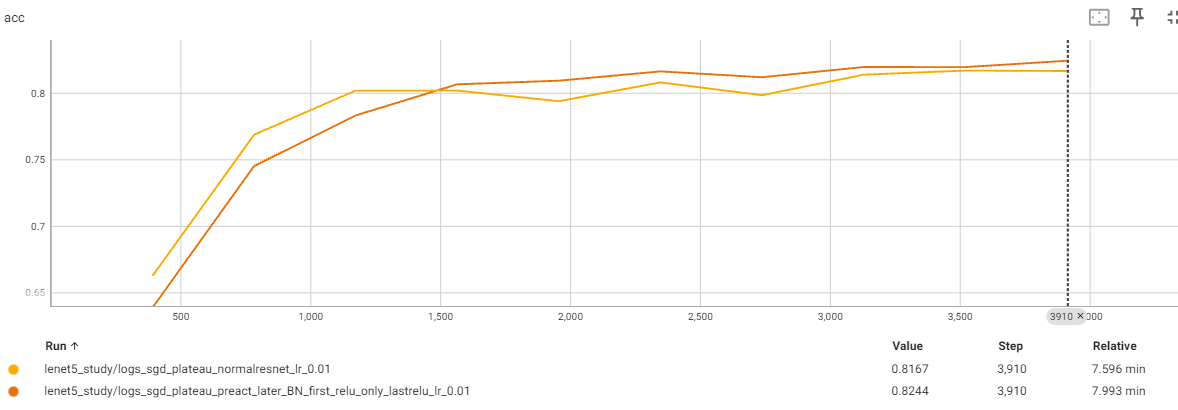
반면에 loss는 preact가 더 높은 것으로 보였다. 이는 논문에서 언급한 BN에 따른 regularization의 영향으로 보인다.