[논문 리뷰 및 구현] MLP-Mixer: An all-MLP Architecture for Vision

pyross·2024년 7월 8일

paper

목록 보기

8/63

Abstract

CNN이 기존 vision 분야에서 자주 사용이 되었지만 최근에는 attention based model 즉 Vision Transformer도 많이 사용이 된다.
이 논문에서는 convolution과 attention이 좋은 성능을 내기에 충분하지만 꼭 필요하지는 않다는 것을 보여준다.
MLP를 베이스로 둔 MLP-Mixer 구조를 제시하는데 2가지의 레이어 타입으로 구성이 되어있다.

각 image patch에 독립적으로 적용이 된 MLP(mixing per-location feature)
patch들 사이를 가로질러서 적용이 된 MLP(mixing spatial information)

대용량의 데이터셋으로 학습이 되었을 때 MLP-mixer는 다른 SOTA 모델과 비슷한 성능을 보여주었다.

1. Introduction

대용량의 데이터와 컴퓨팅 파워의 증가는 패러다임의 변화를 이끌었다.
기존에는 CNN이 사실상 표준으로 적용이 되었지만 최근 Vision Transformer(VIT)의 self-attention based model이 SOTA의 성능을 얻게 되었다.
ViT는 수동으로 visual feature을 얻는 것과 모델의 inductive bias를 없애고 raw data에서 모든 정보를 얻는 것에 의존하게 만들고 있다.

ViT와 inductive bias에 대한 설명은 ViT 논문리뷰에서 작성한 적이 있다.

이 논문에서는 MLP만을 사용한 모델인 MLP-Mixer를 제시한다.
MLP를 반복적으로 spatial location과 feature channel에 적용을 한다.
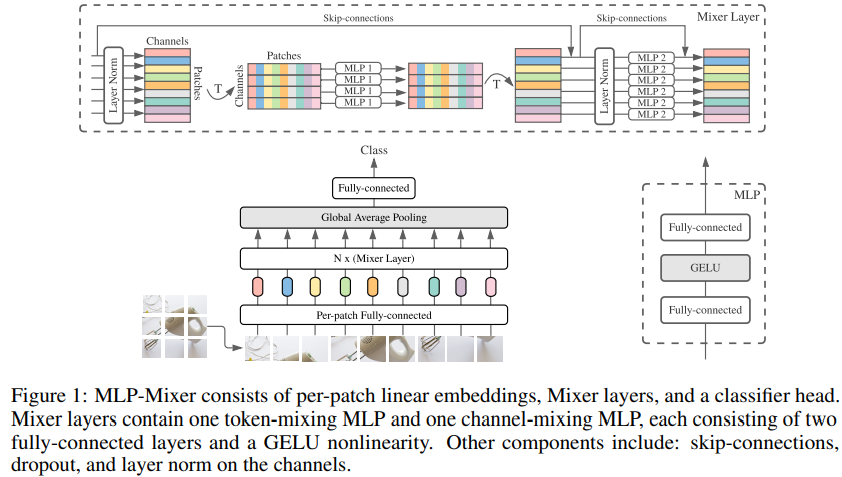위 그림은 MLP-Mixer의 전반적인 그림이다.
input을 Patches $\times$ channel 모양의 linearly projected image patch(token)를 받는다.
그리고 2가지 타입의 MLP가 존재하는데

channel-mixing MLP
token-mixing MLP

channel mixing은 채널간 소통을 가능하게 만들고 각각 독립적은 token의 row를 input으로 받는다.
token-mixing은 다른 spatial location 간의 소통을 가능하게 만들고 각 채널에 독립적으로 동작하고 table의 독립적인 column을 input으로 받는다.
각각의 layer는 Patch $\times$ channel 에서 차원간의 소통을 가능하게 만든다.

극단적으로 이러한 구조는 1x1 CNN의 channel mixing과 depthwise CNN의 token mixing의 조합인 special case로 볼 수 있다. 그러나 반대로 CNN의 Mixer의 special case는 아니다.
거기다 CNN은 MLP의 matrix multiplication보다 더 복잡한 구조를 가진다.

이러한 간단한 구조에도 Mixer는 매우 좋은 성능을 얻었다.
large data(~100M)로 pre-train 되었을 때에는 SOTA의 성능까지 도달하였다.

2. Mixer Architecture

최근 비전분야에서 딥러닝 모델은 다음 feature을 섞는 레이어로 구성되어 있다.

주어진 공간
다른 공간들 사이의 정보
또는 둘다 동시에

CNN에서는 2번 다른 공간들 사이의 정보가 N $\times$ N (N>1)의 convolution과 pooling으로 구현이 된다.
1 $\times$ 1 convolution은 1번 주어진 공간을 섞고 large kernel은 3번 동시에 정보를 섞는다.

Vision Transformer나 다른 attention-based model에서는 self-attention이 3번과 같이 모든 정보를 섞고 MLP가 1번으로 주어진 공간을 섞는다.

Mixer의 주요한 아이디어는 per-location과 cross-location 연산을 분리하는 것이다.

INPUT
Mixer는 input을 S개의 patch로 나누고 각 patch를 linear layer를 통해 hidden dimension $C$ 로 바꾼다.

여기에서 모든 input patch는 같은 projection matrix를 한다.

결국 input은 다음과 같이 구성된다. $\mathbf{X}\in \mathbb{R}^{S\times C}$

input의 형식의 내용은 ViT의 내용과 동일하다.

LAYER
Mixer는 동일한 사이즈의 layer로 구성이 되는데 각 layer는 2개의 MLP block으로 구성이 된다.

우선 처음 나오는 token-mixing은 column 단위의 연산이 진행이 된다. 즉 $\mathbf{X}^{\mathbf{\top}}$ 에 연산이 적용이 된다.
이 연산의 결과는 $\mathbb{R}^C \rightarrow \mathbb{R}^C$ 으로 되고 column을 공유하게 된다.
두번째는 channel-mixing이고 row 단위로 연산이 된다. 역시 $\mathbb{R}^C \rightarrow \mathbb{R}^C$ 으로 만들고 row를 공유하게 한다.

각 MLP block은 2개의 fully-connected layer와 1개의 nonlinearity로 구성이 되고 각각 row에 독립적으로 적용이된다.

Mixer layer를 수식으로 적으면 다음과 같다.
$\mathbf{U}_{*, i} = \mathbf{X}_{*, i} + \mathbf{W}_2 \sigma (\mathbf{W}_1 \text{LayerNorm}(\mathbf{X})_{*, i}), \quad \text{for } i = 1, \ldots, C$
$\mathbf{Y}_{j, *} = \mathbf{U}_{j, *} + \mathbf{W}_4 \sigma (\mathbf{W}_3 \text{LayerNorm}(\mathbf{U})_{j, *}), \quad \text{for } j = 1, \ldots, S$
여기에서 $\sigma$ 는 (GELU)등의 element-wise nonlinearity이다.

대강 pytorch코드로 순서도를 쓰면 다음과 같을 것이다.

        self.token_mixer = nn.Sequential(
            nn.LayerNorm(),
            nn.Linear(),
            nn.GELU(),
            nn.Linear(),
        )
        self.channel_mixer = nn.Sequential(
            nn.LayerNorm(),
            nn.Linear(),
            nn.GELU(),
            nn.Linear(),
        )

그리고 $D_S$ 와 $D_C$ 는 각각 token-mixing, channel-mixing MLP의 조절이 가능한 hidden width다.

$D_S$ 는 위에서 적었듯이 input patch의 숫자이다. 그렇기 때문에 계산량도 $D_S$ 에 linear하게 늘어난다. (ViT는 quadratic하게 증가한다.)
$D_C$ 는 patch size에 independent하기 때문에 전반적인 복잡도는 이미지의 pixel에 linear하다. CNN과 비슷하다.

또한 channel-mixing MLP와 token-mixing MLP는 동일한 param이 긱 row, col에 사용이 된다.

이 부분에 대해서 이해를 해보자면
channel-mixing을 matrix 곱으로 표현을 하면 아래와 같다.
직접 그린 그림인데
여기에서 1, 2, 3이 W의 4, 8, 5와 dot-product가 되는데
4, 8, 5는 아래의 4, 5, 6과도 동일하게 dot-product가 이루어진다.
결국 param을 공유하는 것이다.

이러한 patch들 사이의 param의 공유는 cnn의 중요한 가정 중 하나인 positional invariance를 제공한다.

positional invariance는 사물의 위치가 바뀌어도 동일한 패턴을 보인다는 것이다.
CNN에서는 하나의 filter가 동일한 param을 가지고 돌아다니면서 여러곳을 찍기 때문에 같은 object가 어디에 있든지 동일한 패턴을 얻을 수 있다.

그러나 token-mixing에서 진행되는 채널들 간의 param의 공유는 일반적이지 않다.
param의 공유는 $C$ 나 $S$ 가 증가하였을 때 architecture이 너무 빨리 자라는 것을 막고 메모리를 아낄 수 있다.
또한 이러한 공유는 실질적인 성능에 영향을 미치지 않는다.

모든 MLP-Mixer의 layer는 동일한 크기를 가진다. 이는 transformer와 비슷하고 피라미드식인 CNN과는 다르다 크기를 유지한다.
또한 Mixer는 skip-connection과 layer Normalization을 채택하였다.
그리고 ViT와는 다르게 positional embedding을 적용하지 않았는데 token-mixing MLP는 patch의 위치에 sensitive해서 위치를 알 수 있기 때문이다.
마지막으로 global averaging pool과 linear classification head가 연결된다.

3. Experiment

MLP-Mixer 모델을 중간 크기부터 큰 크기까지 pretrain을 하고 small 부터 mid-size의 downstream classification task에 적용을 하여서 평가를 하였다.
평가 요소는 3가지로 다음과 같다.

downstream task의 정확도
pre-training의 total-computation cost
test-time throughput

Downstream task
ImageNet, Cifar10 등 등 유명한 downstream task data 사용

Pre-training
pre-training을 먼저하고 fine-tune을 하는 식으로 transfer learning의 표준을 따름

pre-training은 2개의 데이터로 구성이 됨

ImageNet-21K: 21k class with 14M image
JFT-300M: 18k class with 300M image

pre-train은

224 해상도와
Adam, $\beta_1=0.9, \beta_2=0.999$
linear warmup 10k step
linear decay
batch size 4096
weight decay
gradient clipping 1

JFT-300M은 이미지를 cropping technique, random horizontal flipping으로 전처리함.
ImageNet data는 dada augmentation, regularization technique를 적용함. 예를 들어 RandAugment, mixup, dropout, stochastic depth 등을 사용

Fine-tuning
Fine-tune은

SGD with momentum
batch size 512
gradient clipping 1
cosing learning rate with linear warmup

Fine-tune에서는 weight decay를 사용하지 않았다.

또한 보통 fine-tune 과정에서 pre-train보다 더 높은 해상도를 사용해서 fine-tune을 진행하는데 이 때에 patch의 size는 고정이 되어있기 때문에 patch의 숫자가 더 늘어나게 되고 (S에서 S'으로) 이에 따라서 token-mixing MLP의 block을 수정해줘야 했다.
여기에서 논문의 부록의 설명에 따르면 만약 해상도가 $K$ 배 증가하게 된다면 patch의 숫자 S는 $K^2$ 으로 증가를 하게 된다.
이 때 hidden width $D_S$ 의 크기 역시 $K^2$ 배로 늘려주고 이 MLP를 pre-trained MLP로 가중치를 초기화하기 위해서는 input sequence를 $K^2$ 개로 나눠주면 원본의 S개의 길이가 나오게 되는데 각각 새로운 MLP를 각 S개의 part에 따라서 병렬적으로 동작이 가능하게 pretrained MLP의 가중치로 초기화 시켜주면 된다.
그림으로 설명하면 다음과 같다.
기존의 연산이 위와 같다고 생각했을 때 $K=2$ 즉 patch의 숫자가 4배가 되었다고 가정하면
이렇게 각각의 부분에 대응되게 가중치를 늘려서 할당한다.
그럼 실제 연산에서 병렬적으로 pretrained 된 가중치가 작용을 한다.

이를 수식으로 $\mathbf{W_1}\in\mathbb{R}^{D_S\times S}$ 에서 $\mathbf{W_1}\in\mathbb{R}^{({K^2\cdot D_S})\times (K^2\cdot S)}$ 가 된다고 적혀있다.

Metrics
평가는 모델의 computational cost - quality의 관계를 평가하였다.
2가지의 평가 기준이 있는데

TPU-v3를 활용하였을 때의 총 pre-training 시간: FLOPs와 학습 효율성, 데이터의 효율성의 복합적인 평가
TPU-v3에서의 images/sec/core의 throuphput

모델의 quality는 top-1 downstream accuracy로 평가

Models
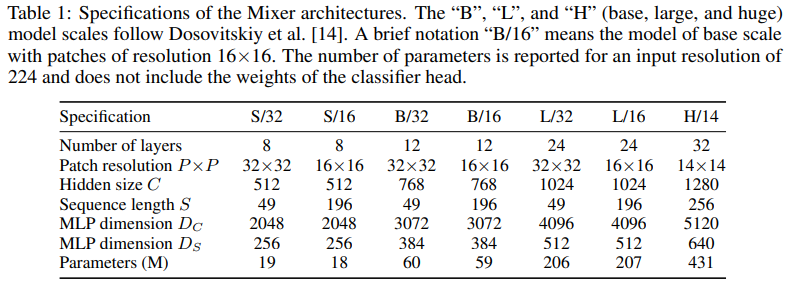다양한 종류의 세팅을 가지고 모델을 평가
비교 모델은 CNN-based model, attention-based model로 구성

3.1 Main Results

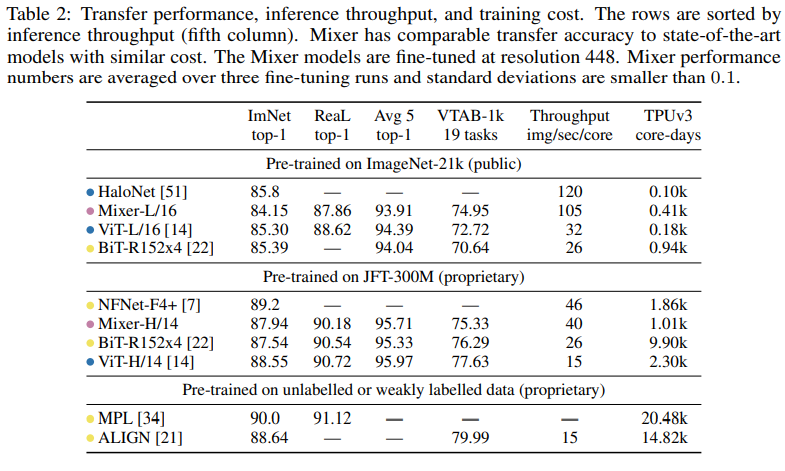놀랍게도 MLP만으로도 CNN, attention based SOTA모델과 비슷한 성능을 보였다.

논문에서 Mixer는 ImageNet-21k로 pretrain하는 과정에서 regularizatioin이 없으면 overfitting이 되었다고 한다. ViT도 overfitting되는 경향이 있었다고 함.

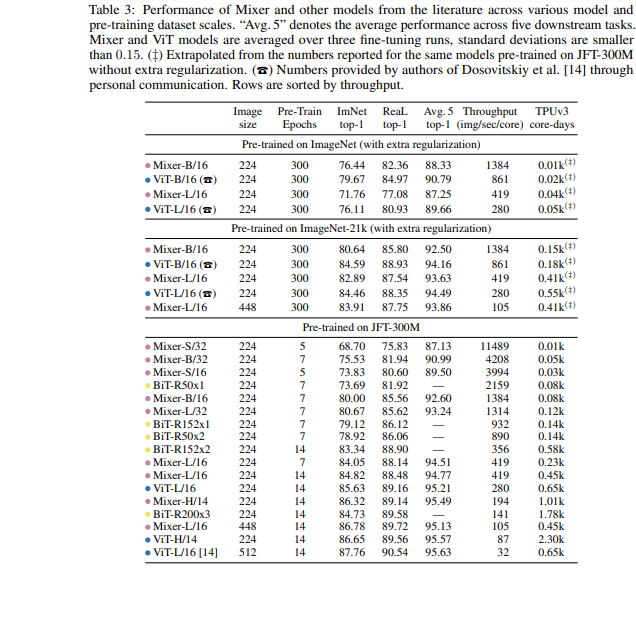
pre train 데이터의 크기가 증가할수록 Mixer는 많은 성능향상을 보였다고 함. 실제 위표에서 JFT로 학습이 된 경우 BiT 모델을 0.4%로 이기고 ViT랑은 0.6% 정도밖에 차이가 나질 않는다. 이는 적은 데이터에서 보다 많은 향상이 있었음을 보임

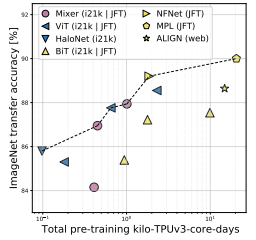또한 학습에 드는 연산량-정확도의 측면에서도 Mixer는 다른 SOTA 모델에 비교할만한 결과를 보임. 또한 위 그림은 total pre-training cost와 accuracy간 상관관계를 보여줌

3.2 The role of the model scale

앞에서는 큰 모델에 대해서 봤다면 작은 모델을 중점으로 봐보자.

우리는 2가지 독립적인 방법으로 모델의 크기를 조절할 수 있다.

pre-training 단계부터 모델의 크기(number of layer, hidden dim, MLP width)를 늘린다.
fine-tune 단계에서 image의 해상도를 늘린다.

전자는 pre-training의 compute와 throughput 모두 영향을 미치지만 후자는 throughput에만 영향을 미친다.
결과는 위와 같다.
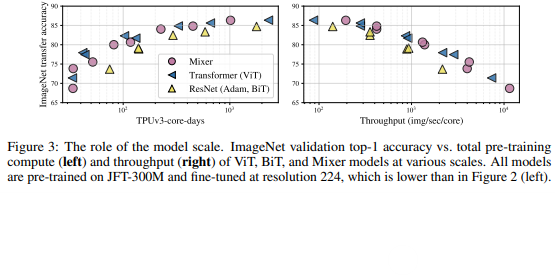그림으로 표현하면 위와 같은데 Mixer는 pre-training data의 크기가 증가하면 성능이 점점 증가하는 모습을 보여주고 더 큰 throughput을 보여준다.

3.3 The role of the pre-training dataset size

앞서 언급했다시피 pre-training dataset의 size가 커지면 Mixer의 성능이 많이 증가하는 것을 알 수 있는데 여기에서 영향에 대해서 다룬다.

다양한 모델을 pre-training dataset의 size를 다르게 하고 epoch를 조절해서 총 step은 동일하게 만들어서 비교를 하였는데
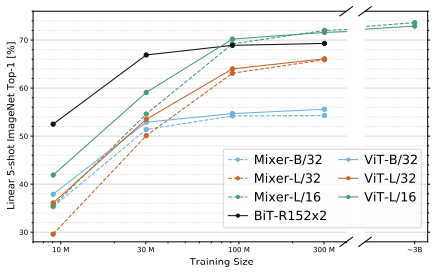점선을 보면 가장 작은 데이터에는 Mixer가 overfitting을 보여주어서 성능이 떨어지는데 BiT 모델도 overfitting이 된 것을 보면 convolution의 inductive bias가 너무 강해서 그런 것으로 생각된다.

데이터가 점점 증가하면 성능이 빠르게 증가하여 마지막에 3B의 가장 큰 데이터에서는 ViT를 이기는 모습을 보여준다.
이는 Mixer가 data scale의 benefit을 ViT보다도 더 얻는 것으로 보인다.

3.4 Invariance to input permutations

이번에는 Mixer와 CNN의 inductive bias의 차이를 공부해보았다.

Mixer-B/16과 ResNet50x1 모델을 JFT-300M으로 pre-training을 진행하였는데 input을 다르게 하였다.
input의 변형 방법은 2가지인데

16x16 patch의 순서를 섞고 공유 순열로 각 패치 내의 픽셀을 바꾼다.
전체 이미지에서 픽셀을 섞는다.

섞는 방법을 적용하면 이렇게 된다.

결과는 다음과 같은데
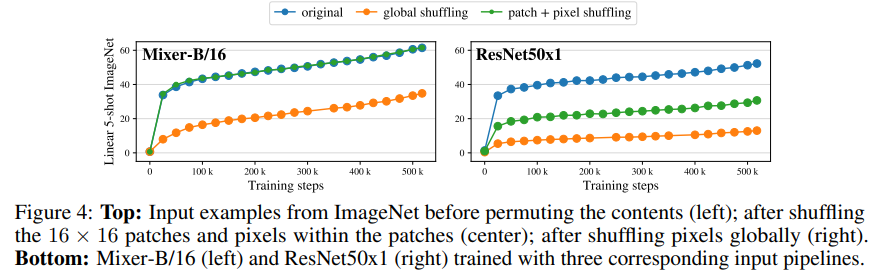Mixer는 patch와 pixel을 같이 섞었을 때에는 성능 저하가 일어나지 않았다.
왜냐하면 MLP가 채널, patch 각각 독립적으로 작동해서 데이터를 학습하기 때문에 성능을 얻는데에 상관이 없다.
그러나 CNN은 이미지 pixel의 순서에 inductive bias를 의존하기 때문에 성능이 매우 떨어진다.
추가로 global permutationg에서 CNN은 75%로 매우 많은 성능저하가 일어났지만 Mixer는 45%로 매우 적었다.

3.5 Visualization

CNN의 첫번째 layer는 gabor filter와 같은 모습을 보이며 이미지의 지역적인 부분에 작용을 한다.

gabor filter는 간단하게 설명하자면이런 모양으로 이미지의 외곽선을 주로 추출할 때 사용된다고 한다.

반면에 Mixer는 token-mixing MLP를 통해 global information change를 가능하게 만드는데 여기에서 궁금한 부분이 생긴다.

MLP도 비슷하게 작동할까?
위 그림은 token-mixing MLP의 첫번째, 두번째 세번째 hidden unit이다.
Mixer는 모든 token에 영향을 주기 때문에 특정 부분은 전체 이미지에 적용이 되고 어느 부분은 이미지의 부분에 적용이 된다.
위 그림을 보면 CNN의 gabor filter와 비슷하게 특정 부분만 색이 강하고 특정 부분은 약하다.
이를 통해 특징을 추출할 수 있다.

5. Conclusion

이 논문에서는 vision 분야에서 MLP만을 활용한 매우 간단한 모델로도 SOTA의 attention, CNN기반 모델과 비슷한 성능을 보이는 것을 보였다.

6. 구현

cifar10 데이터를 위한 3x32x32 데이터 형식을 바탕으로 모델을 구현했다.

class MixerLayer(nn.Module):
    def __init__(self, d_channel=512, d_token=512):
        super().__init__()
        self.norm1 = nn.LayerNorm(d_channel)
        self.norm2 = nn.LayerNorm(d_channel)

        self.token_mlp = nn.Sequential(
            nn.Linear(d_token, d_token),
            nn.GELU(),
            nn.Linear(d_token, d_token)
        )
        self.channel_mlp = nn.Sequential(
            nn.Linear(d_channel, d_channel),
            nn.GELU(),
            nn.Linear(d_channel, d_channel)
        )

    def forward(self, x):
        # x shape: (batch, d_token, d_channel)
        residual = x
        x = self.norm1(x)
        x = self.token_mlp(x.transpose(1, 2)).transpose(1, 2)
        x = x + residual

        residual = x
        x = self.norm2(x)
        x = self.channel_mlp(x)
        x = x + residual
        return x


class MLPMixer(nn.Module):
    def __init__(self, image_size=32, patch_size=4, channel_size=3, num_layer=8, d_channel=512, class_num=10):
        super().__init__()
        self.channel_size = channel_size
        self.image_size = image_size
        self.patch_size = patch_size

        self.patch_num = (image_size//patch_size)**2
        self.input = nn.Linear(channel_size*patch_size**2, d_channel)

        self.layer = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)',
                      p1=patch_size, p2=patch_size),
            nn.Linear(channel_size*patch_size**2, d_channel),
            *[MixerLayer(d_channel, self.patch_num) for _ in range(num_layer)],
            nn.LayerNorm(d_channel),
            Reduce('b n c -> b c', 'mean'),
            nn.Linear(d_channel, class_num)
        )

    def forward(self, x):
        x = self.layer(x)
        return x