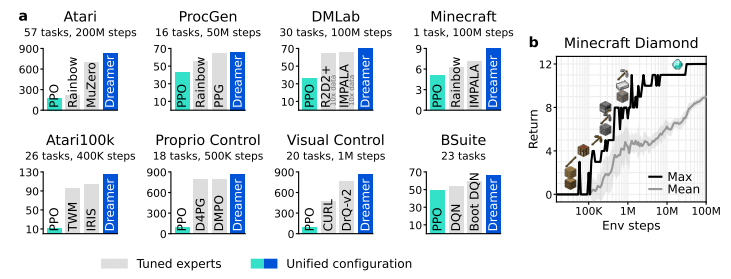
요약
Dreamer를 다양한 domain에 fixed hyper param으로 robust하게 적용하기 위해 여러 trick을 넣은 것을 설명하는 논문이다.
빠르게 정리해보자면
world model의 경우
- KL의 free bit 추가
- KL 비율 체계화 (dyn에 1, rep는 0.1)
- categorical distribution의 1% uniform 추가
- symlog를 통한 observation vector 변환
critic의 경우
- critic의 exponential categorical distribution화
- target critic의 EMA (사실 이건 나도 dreamer v2를 보고 왜 안쓰지 생각했다.)
- replay buffer의 trajectoriy와 imagine의 trajectory의 다른 β
- output matrix zero
actor의 경우
- 기존의 imagination reuturn을 직접 미분하는 것이 사라지고 reinforce + entropy만으로 학습
- advantage를 사용하는 것은 동일하나 이를 max(1,S)로 낮은 reward는 그대로 두고 높은 reward는 낮추는 식으로 변화를 주었다.
전반적으로 prediction에서
- vector observation의 경우 decoder와 encoder의 input과 output에서 symlog를 거친 것을 사용.
- reward와 critic에서는 two-shot loss를 활용해서 gradient와 target scale을 분리.
등등을 개선하고 다양한 domain에서 robust한 성능을 얻음!
개인적으로 마인크래프트에서 다이아몬드 찾는 agent가 제일 신기했다.
Abstract
다양한 task들에서 outperform한 dreamer v3를 제시한다.
dreamer는 environment의 model을 학습하고 이를 통해 agent를 imagination 속에서 학습한다.
이때 normalization, balancing, transformation을 토대로 robustness 기법을 넣어서 안정적인 학습이 가능하다.
특이한건 dreamer는 마인크래프트에서 사람의 데이터 없이 다이아몬드를 채굴할 수 있다고 한다.
이는 엄청나게 멀고 sparse한 reward를 계획을 세워서 진행할 수 있는 인공지능을 의미한다.
Introduction
강화학습 알고리즘은 보통 특정 domain에 specific하게 잘 작동한다.
특정 알고리즘을 다른 domain에 적용하기 위해서는 많은 비용과 노력이 소모된다.
(예: video game taks의 알고리즘을 robotic task에 적용)
별다른 수정 없이 새로운 domain에 적용할 수 있는 일반적인 알고리즘은 인공지능의 중심적인 과제이다.
이 논문은 Dreamer v3를 제시한다. dreamer v3는 다양한 domain에서 고정된 hyper param으로 outperform하는 성능을 내었다.
dreamer는 model을 학습하고 이를 통해 imagination에서 agent를 학습한다.
지금 어떤 행동을 해야 미래에 좋은 결과가 나올지 고민하는 사람과 동일하다.
예를 들어: 주변 이야기를 들어보고(model 학습) 나중에 어떻게 될지 상상해본다음(model 예측, critic 예측) 공부를 해야 겠다고 마음먹은 고등학생(actor 행동)
그러나 world model을 robust하게 학습하고 이를 활용하는 것은 어려운 문제이다.
dreamer는 이를 normalization, balancing, and transformations 등의 기술을 활용해서 극복했다.
재밌는건 model의 size가 크면 더 좋은 점수를 낼 뿐만 아니라 interaction의 요구량도 줄어들었다고 한다.
dreamer는 처음으로 minecraft에서 다이아몬드를 사람 데이터 없이 해결할 수 있었다.
Learning algorithm
Dreamer v3는 이전과 동일하게
world model, actor, critic으로 구성이 된다.
이때 다양한 domain에서 적용을 할 수 있으려면 3개의 구성요소는 다양한 크기의 신호를 수용하고 목표 항목을 robust하게 balancing할 수 있어야 한다.
이 챕터에는 world model, ciritc, actor을 소개하고 robust한 loss function, 알 수 없는 크기를 robust하게 예측할 수 있는 tool을 제시한다.
World model learning
조금 정보량이 많다. 그러나 차근차근 보면 이전의 논문에서 나왔던 내용이 대부분이라 어려운게 없다.
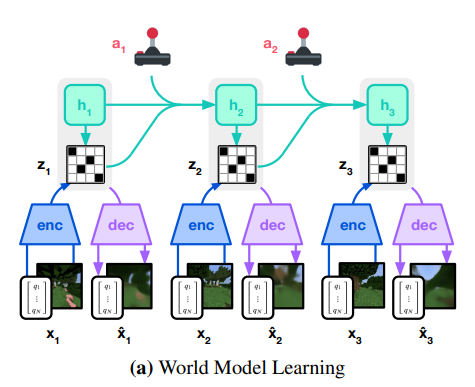 world model은 위와 같이 RSSN(recurrent state space model)로 구성이 된다.
world model은 위와 같이 RSSN(recurrent state space model)로 구성이 된다.
우선 encoder는 를 stochastic representation 로 mapping한다.
이후 recurrent model이 ,을 토대로 를 예측하고 의 concat을 토대로reward, continue(v2의 discount) 를 예측한다.
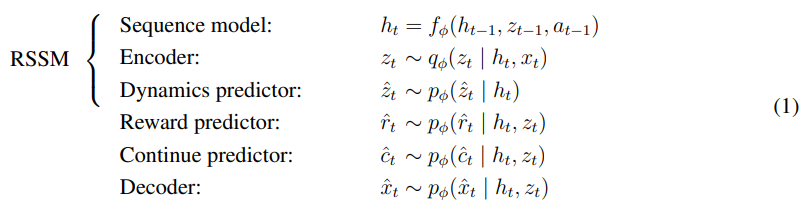 간단하게 위와 같다.
간단하게 위와 같다.
조금 구체적인 구성에 대해서 설명하자면
- encoder: CNN(image input) + MLP(vector input)
- decoder: CNN(image input) + MLP(vector input)
- dynamics, reward, continue: MLP
- Sequence: recurrent
representation은 softmax distribution vector에서 sampling이 되는데 straight-through gradient로 만들어진다.
dreamer v2의 straight-Through
world model의 loss는 아래와 같다.
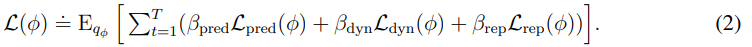 , , 이다.
, , 이다.
보기와는 다르게 내부를 보면 Dreamer V2와 거의 동일하다.
prediction loss는 decoder와 reward predictor를 나중에 나오는 symlog squared loss로 학습하고 continue는 logistic regression으로 학습이 진행된다.
dynamic loss는 next stochastic representation 와 predictor 사이의 KL divergence를 낮추는 방식으로 학습이 된다.
그리고 dreamer v2에서 KL balancing을 주었는데 이와 비슷하지만 조금 다른데 이번 논문은 KL을 stop_grad를 활용해서 비율을 다르게 주지만 각각의 명칭을 dynamic loss와 representation loss로 정했다.
이때 dynamic이 예측이 쉽지만 정보를 조금밖에 못담는 trivial solution을 피하기 위해서 free bit을 추가하였는데
이는 각 손실이 최소한의 정보(1 nat 1.44 bits)를 유지하도록 clipping을 해주어서 정보를 유지하면서도 손실을 관리할 수 있게 만들어준다.
- 간단하게 KL이 너무 낮아지면 posteerior과 prior이 너무 똑같아져서 의미있는 정보가 사라지는 것을 주의하기 위해서 최소한의 기준치를 정함.
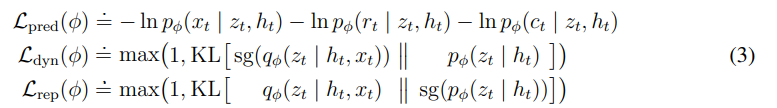 이전의 world model은 representation loss를 visual complexity에 따라서 다르게 줘야 했다. 복잡한 3D 환경은 세부사항은 그다지 중요하지 않기 때문에 예측하기 쉽게 간단하게 만들기 위해 강하게 regularization을 했고 복잡하지 않은 Atari같은 2D 환경이나 배경이 고정되어 있는 환경은 detail을 뽑아내기 위해서 하나하나의 pixel이 중요하게 의미하기 때문에 regularize를 약하게 줬다.
이전의 world model은 representation loss를 visual complexity에 따라서 다르게 줘야 했다. 복잡한 3D 환경은 세부사항은 그다지 중요하지 않기 때문에 예측하기 쉽게 간단하게 만들기 위해 강하게 regularization을 했고 복잡하지 않은 Atari같은 2D 환경이나 배경이 고정되어 있는 환경은 detail을 뽑아내기 위해서 하나하나의 pixel이 중요하게 의미하기 때문에 regularize를 약하게 줬다.
그러나 이제 위처럼 free bit과 representation loss를 적게 줌으로써 정보를 효과적으로 간직하는 동시에 예측이 쉽게 되기 때문에 fixed hyper param을 통한 다양한 domain의 학습이 가능해졌다.
게다가 추후 설명될 symlog 함수를 사용해서 observation vector를 변환시킴으로써 large input과 large reconstruction gradient를 막고 학습을 안정화 시킬 수 있었다.
추가로 초기 실험에서 KL loss의 spike가 관찰이 되었는데 이는 deep variational autoencoder의 결과와 같았다고 한다.
이를 막기 위해서 encoder와 dynamic predictor의 categorical distribution을 1%의 uniform과 99% network output으로 구성함으로써 deterministic일 수가 없게 만들어서 KL loss의 spike를 막았다고 한다.import torch from torch import Tensor from torch.distributions.utils import probs_to_logits def uniform_mix(self, logits: Tensor, unimix: float = 0.01) -> Tensor: if unimix > 0.0: # compute probs from the logits probs = logits.softmax(dim=-1) # compute uniform probs uniform = torch.ones_like(probs) / probs.shape[-1] # mix the NN probs with the uniform probs probs = (1 - unimix) * probs + unimix * uniform # compute the new logits logits = probs_to_logits(probs) return logits이런 느낌일 것이다.
바뀐 사항
기존에서 추가된 부분은
- KL의 free bit 추가
- KL 비율 체계화 (dyn에 1, rep는 0.1)
- categorical distribution의 1% uniform 추가
- symlog를 통한 observation vector 변환
Critic learning
actor과 critic은 환경의 상태 을 바탕으로 예측한다.
actor은 을 최대화하는 것이 목표다. 이때 로 줬다고 한다.
prediction horizon 로 줬다고 한다.
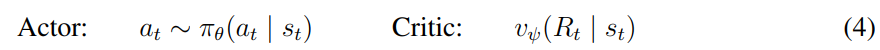 actor은 stochastic하고 Critic은 deterministic하다.
actor은 stochastic하고 Critic은 deterministic하다.
replayed input에서 만들어진 representation에서 imagine을 진행해서
imagine state , action , rewards , continuation flag 를 예측한다.
이때 critic이 학습하는 값은 -return을 계산하고 이를 통해 를 예측하고 critic으로 학습한다.
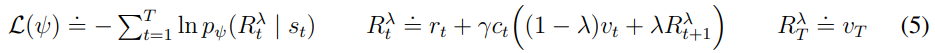
critic은 간단하게 parameterized된 normal distribution이 될 수도 있지만
실제로 반환되는 분포가 다양한 모드가 될수도 있고 environment의 크기에 따라서 dense나 sparse하게 바뀔 수도 있다.
논문에서는 mode의 예시를 들었는데 이는 찾아보니 특정 행동을 하였을 때 이기거나 지거나의 상황은 단일 mode이다. 이는 normal distribution으로 표현할 수 있다.
그러나 로봇이 특정 행동을 해서 결과를 얻는 것은 가능한 행동이 매우 많고 상황도 매우 많기에 이는 multiple mode이다. 이를 표현하기 위해서 categorical distribution이 필요하다.
출처: 구글 리서치 블로그
그렇기 때문에 학습을 안정화 하기 위해서 critic을 이전의 state처럼 categorical distribution으로 만드는데 exponentially spaced bin을 활용해서 gradient의 scale과 prediction target을 분리했다고 한다.
이 부분은 아래 robust prediction 부분의 two shot encoding을 보면 이해가 쉽다.
reward를 예측하기 힘든 환경에서 value를 예측을 개선하기 위해서 critic loss를 imagined trajectories에는 로 주었고 replay buffer의 trajectories에는 으로 주었다. 이를 on-policy로 -return을 이용해서 학습한다.
critic이 자기 자신의 target을 예측하기 때문에 이를 안정화하기 위해서 EMA를 사용한 momentum을 predict하게 바꾸었다.
이는 그냥 byol이라고 생각하면 될 것 같다.
추가로 학습 초기에 critic과 reward predictor이 random init이 되어있어서 이상한 보상을 주는 것이 bias를 주어서 이를 막기 위해서 output weight matrix를 0으로 init하고 시작하였다고 한다.
바뀐 사항
기존의 dreamer에서 추가된 부분은
- critic의 exponential categorical distribution화
- target critic의 EMA (사실 이건 나도 dreamer v2를 보고 왜 안쓰지 생각했다.)
- replay buffer의 trajectoriy와 imagine의 trajectory의 다른
- output matrix zero
Actor learning
dreamer v2에서 actor의 학습에 entropy regularization을 넣어주었다.
그런데 이러한 entropy regularization가 정확하게 측정하려면 environment reward의 빈도와 sacle에 의존한다.
- 이상적으로 reward가 sparse하면 agent를 더 많이 탐색하고 dense하면 더 많이 정보를 exploit해야 한다.
- 동시에 환경의 reward scaling하는 것이 탐색의 기회에 영향을 주면 안된다.
이는 return sacale을 normalize하는 동시에 reward frequency의 정보를 보존해야 한다는 것을 의미한다.
(regularizer는 scale과 frequency 동시에 영향을 받기 때문)
dreamer의 fixed entropy scale 를 다양한 도메인에 사용하기 위해서 return을 사이의 범위로 normalize해야 한다.
이때 return에서 offset을 빼는 것은 actor의 gradient에 영향을 주지 않음 (advantage) 그렇기 때문에 이를 빼주고 S로 나누는 것으로 충분하다고 함.
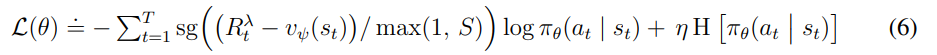 loss는 위와 같이 구성이 된다.
loss는 위와 같이 구성이 된다.
Advantage를 구하고 이를 normalize하기 위해서 나눠주는데 이때 S는 아래에 설명할 범위이다. max(1,S)의 의미는 S 범위가 1보다 작으면 즉 reward의 최대-최소 범위가 1보다 작을정도로 매우 작으면 그냥 그 reward를 둔다는 의미이다.
이는 너무 큰 reward의 영향을 줄이는 동시에 작은 reward가 너무 작아져서 정보량이 줄어드는 것을 막기 위함이다.
그리고 큰 reward를 줄이는 것은 괜찮지만 너무 작은 reward를 키우게 된다면 noise를 높일 수도 있다고 한다.
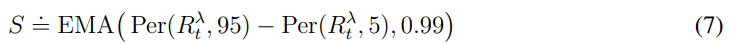 위 식은 normalize를 위한 scaling S에 대한 식이다.
위 식은 normalize를 위한 scaling S에 대한 식이다.
환경마다 얻을 수 있는 보상이 다른데 특정한 random하게 구성된 환경에서 보편적이지 않은 몇몇 episode가 많은 양의 return을 얻을 수 있을 때 이때의 smallest와 largest를 return 통해서 normalize하게 된다면 return이 너무 작아지게 된다.
S는 95%와 5% 사이의 범위를 가지고 나눠주게 되는데 이때 이전의 target network를 0.99의 EMA로 한다고 언급했듯이 S를 EMA를 가지고 함으로써 너무 큰 변화룰 주지 않고 매끄럽게 만들어준다.
- 이전의 논문들은 return 대신 advantage를 normalize하는데 이는 reward가 도달할 수 있는지 여부는 상관 없이 return의 maximizing을 고정된 정도로 강조하는 것이다.(사실 이 설명은 와닿지는 않는다.)
- 또한 sparse한 경우 advantage를 scaling up하게 된다면 작은 값도 normalize가 되면서 커지게 되어 noise를 증폭하게 되고 이는 entropy를 능가해 학습이 어려워지게 만든다.
- 또한 reward나 return을 표준편차로 normalize하게 된다면 역시 sparse한 경우 std가 0에 가깝기에 엄청나게 증폭이 되어 문제가 된다.
- constrained optimization은 entropy를 고정된 것을 목표로 하는데 이는 sparse한 reward와 dense한 reward의 경우 entropy가 커서 수렴이 잘 안된다.
논문의 저자는 분모를 제한 + return normalization을 사용하여서 이러한 문제를 극복했다고 한다.
재밌는 것을 발견했는데
return을 normalize한다고 되어있는데 사실 정확한 수식의 설명은 advantage를 return을 가지고 normalize한다.
그래서 엥? 잘못봤나 싶었데 dreamer v3논문의 v1 버전 즉, 초창기 논문 버전에서는위와 같은 수식이었다.
추가된 부분
actor에서 추가된 부분은
- 기존의 imagination reuturn을 직접 미분하는 것이 사라지고 reinforce + entropy만으로 학습
- advantage를 사용하는 것은 동일하나 이를 max(1,S)로 낮은 reward는 그대로 두고 높은 reward는 낮추는 식으로 변화를 주었다.
Robust predictions
이 부분도 바뀐 것이 많은데
input을 복구하고 reward, return을 예측하는 것은 domain마다 quantity의 scale이 달라서 어렵다.
또한 MSE 등을 사용하면 큰 타겟을 학습하는 과정에서 발산할 수 있으며 절대 손실은 정체가 발생할 수 있다.
이 논문은 Symlog squared error으로 해답을 제시한다.
우선 Symlog란 무엇일까?
왼쪽은 symlog로 sign은 양수면 +1, 음수면 -1을 반환한다. 오른쪽은 symexp로 symlog로 만든 값을 원본으로 복구할 수 있다.
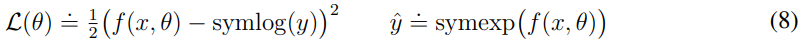 위와 같이 예측하는 target을 symlog를 통해서 압축하는 것이다. 는 symlog로 학습한 output을 원본 예측으로 복구하기 위한 것이다.
위와 같이 예측하는 target을 symlog를 통해서 압축하는 것이다. 는 symlog로 학습한 output을 원본 예측으로 복구하기 위한 것이다.
즉 학습할 때에는 압축된 target으로 큰 값을 압축하고 예측할 때에는 이를 풀어서 예측한다.
단순한 log와는 다르게 sign함수로 부호를 유지할 수 있기에 매우 큰 양수와 음수를 압축할 수 있다.
또한 symlog는 매우 작을 때에는 거의 원래 값 그대로 이기 때문에 학습에 영향을 주지 않는다. (log(1+x)미분해서 x=0이면 미분 값이 1이서 사실상 원본과 동일)
reward나 return 같은 확률적인 target의 경우 symexp twohot loss를 사용한다.
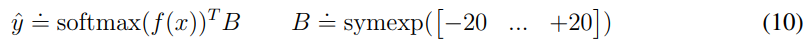 위와 같은데 이는 softmax로 f(x)의 logit의 확률을 구하고 이를 통해서 exponentially spaced bin에 확률이 할당된다. 이를 통해서 각 값들 * 확률로 되기 때문에 연속적인 값을 output으로 낼 수 있다.
위와 같은데 이는 softmax로 f(x)의 logit의 확률을 구하고 이를 통해서 exponentially spaced bin에 확률이 할당된다. 이를 통해서 각 값들 * 확률로 되기 때문에 연속적인 값을 output으로 낼 수 있다.
이를 학습하기 위해서는 network는 two-hot encoded으로 만든 target을 기반으로 학습을 진행한다.
two-hot encoding으로 만드는 방법은 간단하다.
만약 B가 symexp([-2,...,2])이면 이다. 이때 숫자 4를 encoding하고 싶다면 이와 가까운 k, k+1 2개의 index를 제외한 나머지를 0으로 만들고 k와 k+1 index는 가까운 비율 만큼 할당한다.
에서 k는 3이다. 1.71과 6.38의 차이는 4.67이다. 4와 1.71의 차이는 2.29 6.38과 4의 차이는 2.38
즉 2.29/4.67=0.49, 2.38/4.67=0.51
이다.
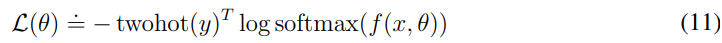 network는 이렇게 twohot으로 이산적으로 만든 target을 학습한다.
network는 이렇게 twohot으로 이산적으로 만든 target을 학습한다.
이때 중요한 것은 이전에 critic에서 예측하는 값을 분포로 나누어서 얻었던 이점인 target과 gradient scale의 분리가 여기에도 들어간다. 손실이 bin의 확률에만 의존하기 때문이다!
이러한 점들을 활용해 Dreamer V3에는 vector observation을 symlog로 바꾸는데
이는 encoder와 input과 decoder의 target에 사용이 된다.
그리고 reward predictor와 critic에는 symexp를 활용한 twoshot loss를 사용하였다.
이를 활용해서 다양한 domain의 빠르고 robust한 학습이 가능해졌다고 한다.
이때 내가 헷갈렸던 부분인데
encoder의 input에 symlog를 하는데 이미지에 symlog를 하는 것은 이상하지 않을까? 보통 이미지는 [0~1]로 정규화가 되어있기 때문이다.
알고보니 vector observation은 속도, 위치 등의 벡터적인 값이었다...# 벡터 관찰 예시 (예: 위치, 속도 등) vector_obs = torch.tensor([100.0, -50.0, 0.5, -0.2]) # 이미지 관찰 예시 image_obs = torch.randn(3, 64, 64) # 3채널의 64x64 이미지
바뀐 부분
이 부분은 사실 설명 파트이다.
- vector observation의 경우 decoder와 encoder의 input과 output에서 symlog를 거친 것을 사용.
- reward와 critic에서는 two-shot loss를 활용해서 gradient와 target scale을 분리.
Results
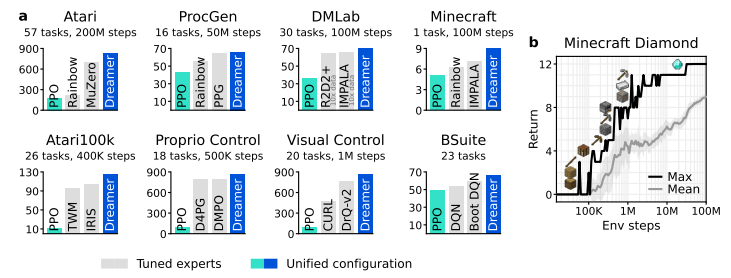 매우 다양한 문제들을 해결할 수 있었고 전반적으로 다른 모델을 압도하였다.
매우 다양한 문제들을 해결할 수 있었고 전반적으로 다른 모델을 압도하였다.

