현재 인턴하고 있는 랩실에서 나온 논문이다.
되게 재밌어서 기록하려고 한다.
논문의 핵심 내용만 다루도록 하겠다.
논문을 이해하기 위해서는 MCTS에 대한 지식이 필요하다.
논문을 예전에 읽었고 작성하는 것이기에 알고있는 내용 위주로 작성 중.
빼먹거나 이상한, 주관적인 부분이 있을 수 있음.
Abstract
Diffusion model은 planning tool로 사용되는데(diffuser 등)
MCTS 등과 같인 test-time compute를 이용한 search 알고리즘은 제대로 나오지 않았다.
이 논문은 이러한 문제를 다루기 위해서 Monte Carlo Tree Diffusion(MCTD)를 제시한다.
Introduction
그냥 나름대로 정리한 전반적인 내용을 설명하겠다.
앞서 설명했다시피 diffusion model에 MCTS 등의 방법을 통해서 search를 하는 방법은 없다.
그러나 이는 diffusion에 MCTS를 적용하기 힘들기 때문인데
MCTS를 적용하기 위해서는 action을 정의할 수 있어야 한다.
또한 diffusion에서는 MCTS에서 중요한 한가지 fix된 state를 정의하는 것이 힘들다.
이 논문은 이러한 문제를 다음과 같은 방법으로 극복한다.
- semi-autoregresive: diffusion forcing으로 앞부분의 action은 fix, 뒷부분의 noise가 많게
- meta-action: guidance level을 action으로 활용
- jumpy rollout: 간단하게 DDIM으로 rollout을 빠르게 진행
diffusion forcing은 noise의 단계가 모든 state에서 동일한게 아니라 앞부분은 noise가 많이 없고 뒷부분은 noise가 많게 독립적으로 적용이 가능한 framework이다. 이 덕분에 casual한 generation이 가능하다.
Method
빠르게 핵심만 적겠다.
3.1. Denoising as Tree-Rollout
간단하게 앞에서 설명한 diffusionf forcing을 적용해서 앞부분부터 차례대로 적용하는데
이제 앞부분이 어느정도 denoising이 되면 state를 node로 fix하는 것이다.
이때 whole trajectory가 (x1,x2,...,xN)까지 있으면 이를 여러개의 sub plan으로 나눈다 (x1,x2,...,xS)로 S개의 block으로...
이후 casual하게 subplan을 생성하면 아래 그림의 node 처럼 된다.
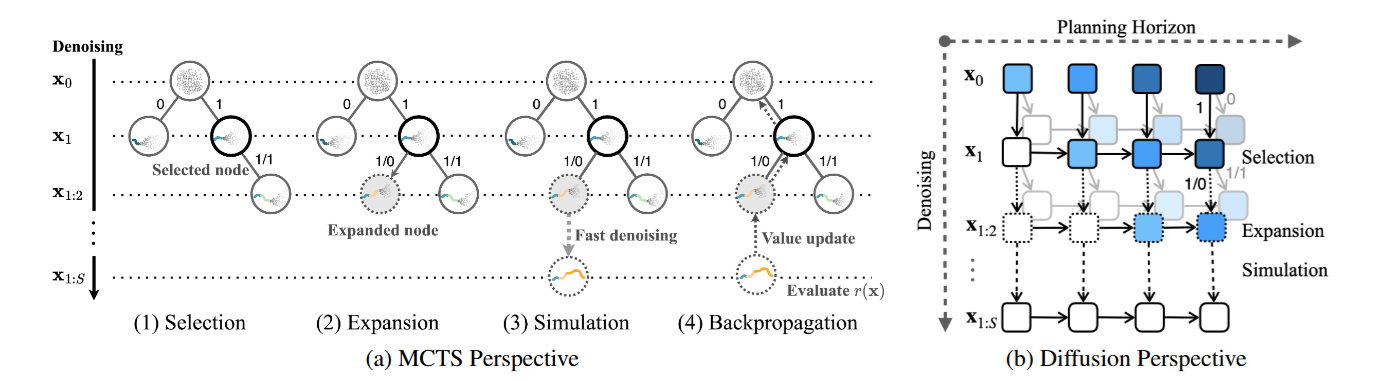
3.2. Guidance Levels as Meta-Actions
이게 나는 이 논문의 핵심이라고 생각한다.
원래 다른 diffusion based MCTS 논문들은 search에서 expansion이 sampling으로 이루어진다.
왜냐하면 diffusion model은 action이 명시적으로 정해지지 않았기 때문.
여기에서 이 논문은 meta-action을 설정한다. meta-action은 generation의 guidance level인데 예를 들어 action이 guidance를 주지 않고 생성, guidance를 주고 생성
이렇게 2개를 고르는 식으로 action을 정할 수 있다.
이때 guidance를 주지 않고 생성하면 explorar이 되는 것이고 guidance를 주고 생성하면 exploitation이 되는 것이다.
나는 이 meta action이 sampling말고 또다른 action을 선택할 수 있는 축을 주는 것으로 생각했고 이래서 meta-action이라고 생각했는데
논문의 저자분에게 이야기해보니 action이 guidance이기 때문에 지금 state 뿐만 아니라 앞에 나올 모든 state에 영향을 주기 때문에 meta-action으로 했다고 하셨다.
그런데 다른 교수님도 나처럼 생각하는거 보면 저 시각도 어느정도 맞는 것 같다.
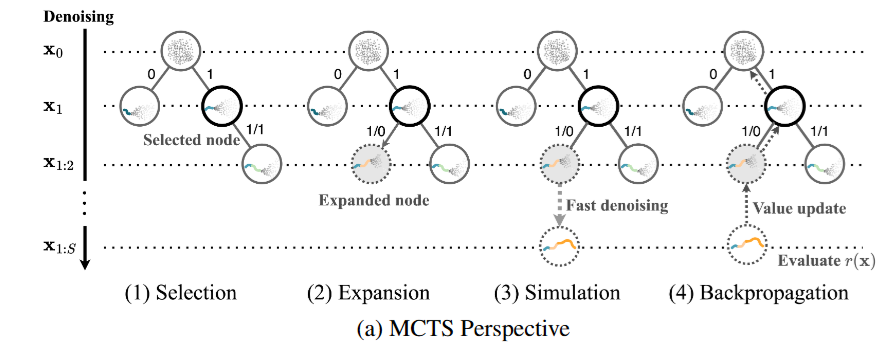결국 위처럼 guidance 0, 1 로 action을 하는 식으로 search를 할 수 있다.
앞서 말했던 subplan으로 생성, meta-action이 합쳐지면 tree의 depth, width가 매우 줄어들기 때문에 search가 효율적이게 된다.
3.3. Jumpy Denoising as Fast Simulation
사실 별거 없다 DDIM으로 를 prediction하기 떄문에 sample의 step을 10, 9, 8 ...으로 하는게 아니라 10, 7, 4...로 빠르게 jumpy해서 rollout을 마칠 수 있다는 것을 의미한다.
정리하면 위와 같이 된다.
Experiments
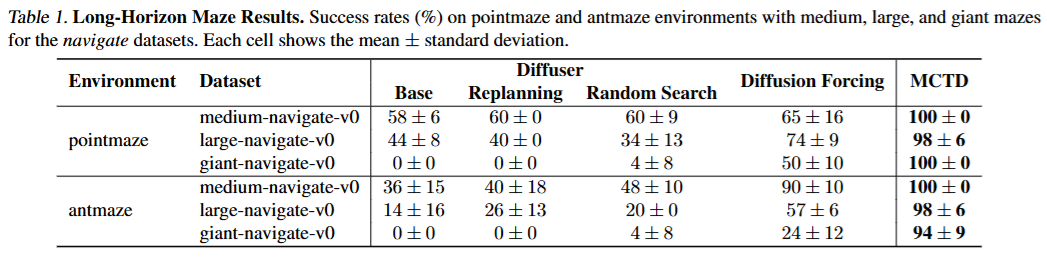maze에서 매우 뛰어난 성능을 보여줌
