[논문 리뷰] SELF-SUPERVISED REPRESENTATION LEARNING FROM RANDOM DATA PROJECTORS - ICLR 2024
paper
요약하자면 self-supervised learning을 통해 학습하는 representation은 다양한 작업에서 활용을 하려고 학습하는 것이다. 이때 projection head가 down-stream task에 중점적으로 학습이 되는데 이를 활용해서
projection head를 여러개 두고 임의의 random downstream task를 구축해서 다양한 downstream task에 활용할 수 있는 representation을 학습하는 것이다.
Abstract
Self-supervised representation learning(SSRL)은 인위적으로 design된 augmentation에서 불변하지 않는 정보를 뽑아내는 것으로 진보해왔다.
이 논문은 augmentation이나 masking에 의존하지 않아 어떠한 데이터와 network 구조에 적용할 수 있는 SSRL 방법론을 제시한다.
random data projection을 재구축하는 과정을 통해서 high-quality representation이 학습가능하다고 보여준다.
1. Introduction
self-supervised learning을 통해 data representation을 학습하는것은 잘 만들어진 pretext task와 관련이 있다.
보통 pretext task는 domain specific한데 사람의 handful assumption이 필요하다.
이때 pretext는 보통 여러개의 view에 transformation invariance assumption을 통한 성능의 향상을 이루어내는데
image 분야의 crop, rotete 등이 대표적이다. 내부 의미는 바뀌지 않기 때문.
그러나 결국 이러한 augmentation은 domain-specific하다.
(가우시안 노이즈는 text에 바로 적용하기 힘듦, 이미지 rotation은 tabular에 적용할 수 없음 등등)
심지어 이미지에서 넓게 사용할 수 있을 것 같던 random resized crop + color jitter도 application-specific한 부분에서는 문제가 발생할 수 있음.
ex) 이미지를 통한 세포 분류 등에서 세포의 색이 바뀌기 때문에 unrealistic example이 만들어짐.
tabular의 경우 augmentation이 random noise addition or random feature swapping으로 제한됨. 그러나 이런 것도 unrealistic example을 만듬.
최근에는 transformation vairance에 의존하는 것이 아니라 masking을 주고 이미지를 재구축 하는 식으로(MAE) 활용을 하거나 NLP에서도 masking을 활용한다.
그러나 이것도 NLP분야에 적용하기 위해서는 이러한 부분에 특화된 transformer와 같은 backbone model이 필요하다.
이 논문은 이러한 domain-specific data augmentation과 특별한 architecture 없는 SSRL 접근법을 제시한다.
대신에 좋은 data representation은 무작위로 만들어진 data projection function을 동시에 재구축하는 과정을 통해서 얻어진다는 놀라운 가설을 통한 학습 방법을 제시한다.
이 내용은 downstream task가 임의의 data projection을 포함할 수 있다는 것부터 시작한다.
만약 random projection 가 주어졌을 때
이때 좋은 representation z를 downstream task에 더 잘 예측할 수 있는 가 존재한다.
이러한 통찰을 바탕으로 representation learning은 무작위 data projection을 투영할 수 있는(다양한 분야에서 사용할 수 있는) representation z와 prediction function 의 조합을 찾는 과정으로 생각할 수 있다.
요약하자면 이 논문은 SSRL을 learning from randomness(LFR) 로 재구성하였다.
LFR의 장점은 random projection function 를 어떤 분야든지 쉽게 구성할 수 있다.
가장 좋은 시작 방법은 neural network를 데이터를 활용하기 쉽게 구성하고 param을 random으로 구성하는 것이다.
3 REPRESENTATION LEARNING FROM RANDOM DATA PROJECTORS
모든 데이터가 같은 feature domain 를 공유하는 raw data 에서
를 학습해서 represent를 만든다.
이때 representation 는 의 임의의 downstream taask 에 활용할 수 있는 유용한 정보를 담고 있어야함.
이때 임의의 prediction function 를 학습할 수 있는데
를 로 바꿀 수 있다.
3.1 PRETEXT TASK: MULTI-OBJECTIVE LEARNING FROM RANDOMNESS
위 내용처럼 representation을 학습하는 목적은 임의의 downstream task에 활용하기 위해서이다.
이때 주로 중요하게 생각되는 downstream task가 있다.
단순이 랜덤 task로부터 representation을 학습하는 것을 통해서 좋은 representation을 얻을 수 있을지는 모르는 일이다.
pretext task는 3가지 요소로 구성된다.
1. representation을 학습하는
2. set of random generated function ,
3. set of simple predictor
로 구성이 된다.
아래 그림과 같다.
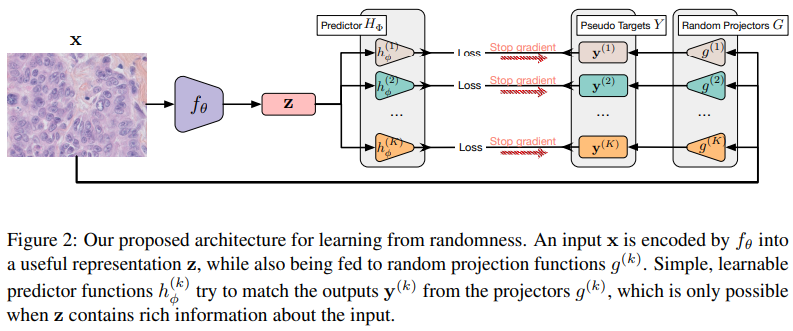 임의의 target Y를 random generator로 만들어내고 이를 predictor 로 예측하는 것이다.
임의의 target Y를 random generator로 만들어내고 이를 predictor 로 예측하는 것이다.
이를 위해서는 가 input에 대한 정보를 최대한 많이 포함하고 있어야 한다.
보다가 든 생각인데
공통된 representation을 활용하는 prediction head를 여러개 달고 여러개의 task를 동시에 활용해서 loss를 구성하면 다양한 분야의 작업에서 공통적으로 중요한 정보만을 담은 representation을 구성할 수 있을 것 같은데 이런 아이디어를 담은 것 같다.
결국 학습은 아래와 같이 구성이 된다.
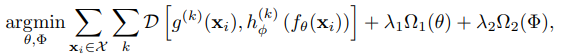 수식에서 는 MSE등 유사도를 가깝게 하기 위한 loss이고 는 regularization이다.
수식에서 는 MSE등 유사도를 가깝게 하기 위한 loss이고 는 regularization이다.
task를 너무 쉽게 구성하지 않기 위해서 는 linear이나 simple neural network with few layer 등으로 간단하게 구성이 되어야한다.
위 수식은 maximum likelihood estimation (MLE)의 lower-bound이다.
우리의 목적은 의 data projection에 대해서 확률을 증가시키는 것이다.
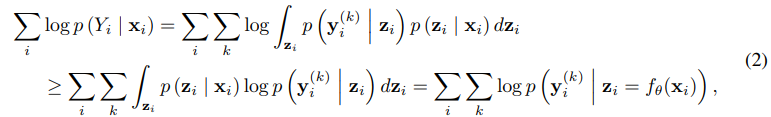 이때 는 representation에 대해서 결정론적이기 때문에 dirac delta distribution이다.
이때 는 representation에 대해서 결정론적이기 때문에 dirac delta distribution이다.
위 두 수식의 조합의 예시로 만약 가 가우시안 분포를 따른다면 (1)의 목적함수는 euclidean distance가 된다.
첫번째 수식을 달성하기 위해서 와 를 동시에 업데이트를 해보았는데 이러한 단순한 학습은 불안정하였다. 그래서 고전적인 EM(expectation-maximization)을 도입하였다.
(2)수식과 같이 MLE를 lower-bound로 생각하고 의 optimization은 E-step으로 간주하였다.
이때 고정된 log-우도 계산 모듈 를 기준으로 사후 분포 를 수정하는 식으로 진행하였다.
말이 어려운데 내 생각에는 representation 에서 나온 예측 값과 에 대한 유사도를 기준으로 representation 영역 를 수정한다는 것 같다.
M-step에서는 representation distribution이 고정이 되고 predictor head 가 최적화 된다.
 수식으로 보면 위와 같다.
수식으로 보면 위와 같다.
이 내용은 이전에 봤던 논문 simsiam의 K-means 설명과 유사하다고 생각한다.
representation update -> predictor update의 반복...
이때 representation model보다 predictor update를 더 자주 반복하면 predictor가 최신 encoder 에 대해서 optimal performance에 가까워진다.
simsiam등 최신 논문에서도 predictor를 optimal하게 update하는 것이 성능 향상을 이끈다고 보였다.
3.2 DIVERGENCE MEASURE: BATCH-WISE BARLOW TWINS
이전에 언급했던 divergence 에 대해서 여러가지의 옵션이 있는데
MSE, Cross Entropy, Contrastive, Triplet 등의 loss가 존재한다.
대부분 다른 point의 차이점을 내타내는 loss이다.
이때 barlow twins loss는
learned representation에서 redundancy를 줄이기 위한 loss이다.
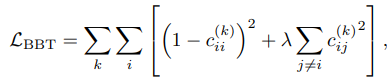
간단하게 batch에서 2개의 view를 만들고 자기의 view(ii)끼리는 가깝게 만들고
다른 sample의 view와는 멀게 만드는 것이다. 이때 중복된 불필요한 정보를 지운다.
는 cosine sim이다.
이를 활용해서 아래와 같이 구성한다.
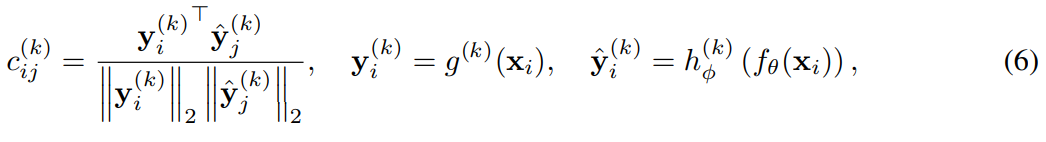 이다.
이다.
이때 원본 barlow twins와 다른 부분은 cosine sim matrix가 원본은 각 dim 로 구성이 되었지만
이 논문은 batch size 에 따라 으로 구성하였다.
원본 barlow twins 구성
3.3 DIVERSITY ENCOURAGEMENT ON RANDOM DATA PROJECTORS
learning from randomness는 간단하게 말해서
로 random한 downstream task를 구성하고 이를 이용해서 representation을 구성하는 것이다.
실제로는 encoder 의 scale을 줄이고 구조를 유지한 채로 weight를 random_init을 통해서 구성해서 사용함.
이때 이렇게 만들어진 함수는 추가적인 다양성을 더해주지 않으면 종종 비슷한 정보를 담는다. 그냥 많이 만들면 brute force와 같이 완화할 수 있지만 이는 computational cost를 증가시키기에 별로이다.
저자는 로 projector를 많이 만들어두고 이를 개 뽑아서 사용하는 방법을 제시한다.
이는 큰 하나의 batch가 random projector에 차이점의 나타내기 충분하다는 것의 가정 하에서 시작한다.
data batch 가 있을 때 각 개의 random generated projector 를 통해서
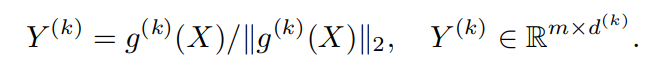 이렇게 normalized 된 output을 만들 수 있고
이렇게 normalized 된 output을 만들 수 있고
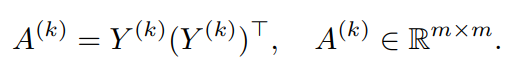 이를 이용해서 각 projector의 batch cosine sim을 구할 수 있다.
이를 이용해서 각 projector의 batch cosine sim을 구할 수 있다.
이 를 flat하게 만들고 normalize하면 을 만들 수 있다.
이는 batch에 대해서 k번째 projector가 작동하는 signature이다.
이를 이용해서 개의 candidate에서 개를 뽑는다.
이때 다음의 이진 제약 최적화 문제를 풀어서 subset 개를 뽑는다.
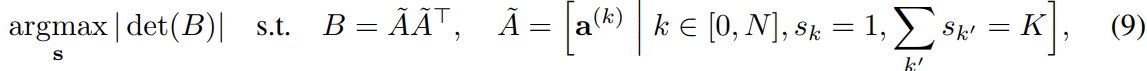 여기에서 이다.
여기에서 이다.
위 수식은 간단하게 개의 projector 중 action matrix가 가장 많이 다른(determinant가 크면 부피가 크니까 각 벡터가 수직에 가까워지니까 달라짐) subset 개를 뽑는 것이다.
위 문제는 NP-hard이지만 Fast Determinantal Point Process와 같이 합리적인 시간 안에 근사할 수 있다.
4 EXPERIMENTS AND EVALUATION
4.2 IMPLEMENTATIONS
모든 테스트는 classification이다.
학습된 frozen representation 위에 supervised 학습한 classifier를 올려서 테스트 진행
result
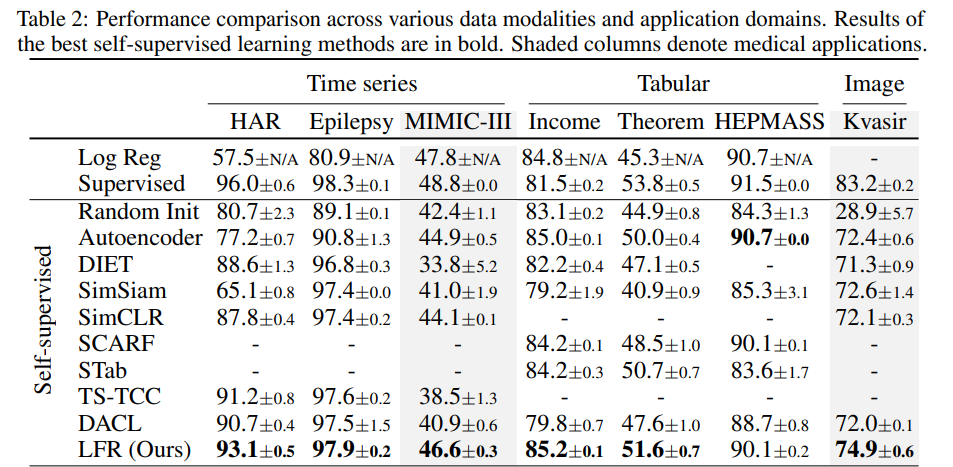 다른 방법과 비교해서 뛰어난 성능을 보여줌
다른 방법과 비교해서 뛰어난 성능을 보여줌
심지어 image augmentation을 적용하기 어려운 domain specific한 MiMiC(medical image)나 tabular에서 좋은 성능을 보임.
4.5 IMPACT OF RANDOM DATA PROJECTOR DIVERSITY
이 부분은 random data projector의 다양성에 대해서 다룬다.
2가지가 중요한데 initialization과 selection이다.
selection은 Determinantal Point Process 이 사용이 되었고
initialization은 2가지의 기술을 적용하였다.
- Beta initialization
- weight dropout
beta 분포는 [0,1]에서 alpha와 beta에 의해서 정의되는 연속확률분포
Beta initialization
alpha=0.5, beta=0.5로 설정해서 cnn의 weight를 -1또는 1로 가깝게 설정
Weight dropout
DropConnect를 활용해서 0.4의 비율로 weight를 끄는 방식으로 weight를 initialization을 한다. 이때 기존과는 다르게 한번 weight를 0으로 진행한 다음에는 얼린다.
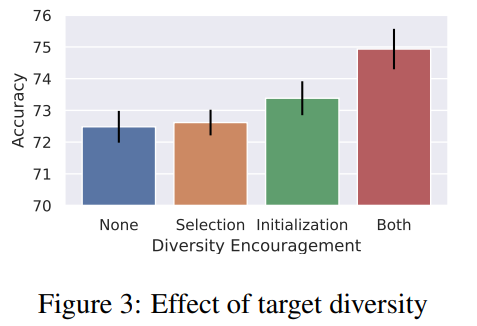 결과는 위와 같다.
결과는 위와 같다.
selection과 initialization을 둘 다 하면 상당히 성능이 향상된다.
4.6 ABLATION STUDY
모델에 영향을 주는 다른 요소들 테스트
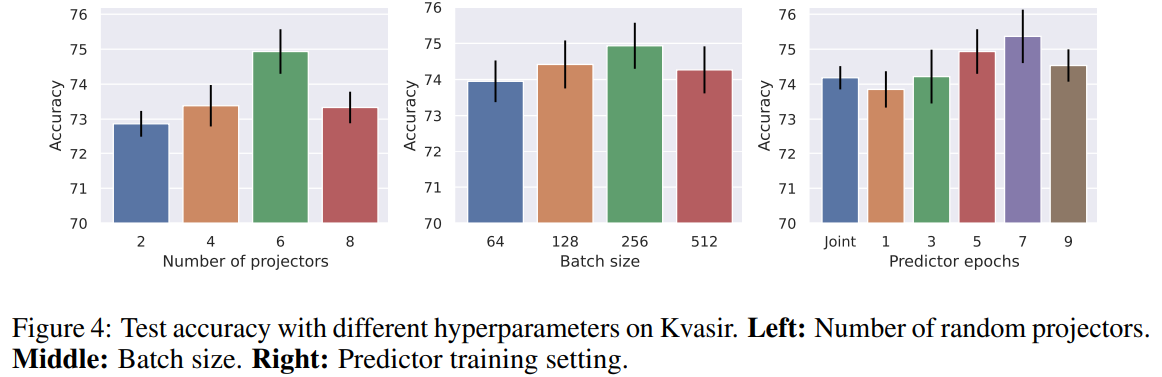
Number of projectors
의 숫자 6일때 가장 좋았다.
6보다 크게 되면 projector에 의해서 동일한 representation이 발생할 확률이 증가하게 되고 이에 따라서 bias가 발생하기 때문으로 봄.
batch size
selection 과정에서 batch size가 중요하게 되는 만큼 batch size도 보았는데 다른 부분에 비해서 상대적으로 큰 변동이 없다. 그래도 256일 때 가장 좋은 성능을 보임.
Predictor training epochs
학습이 predictor과 encoder가 각각 update되고 이때 서로 update되는 epoch의 기준을 바꾸면서 테스트.
joint보다 7 epoch마다 바꾸면서 업데이트를 진행하는게 가장 성능이 좋았음.
optimal한 projector이 더 좋은 representation을 보여주는 모습.
Embedding dimension
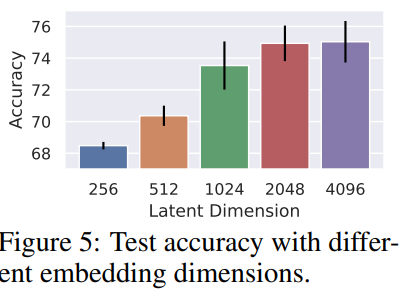 클수록 좋아지는 모습이 보였는데 2048을 넘으면 큰 향상은 안보였다.
클수록 좋아지는 모습이 보였는데 2048을 넘으면 큰 향상은 안보였다.