요약
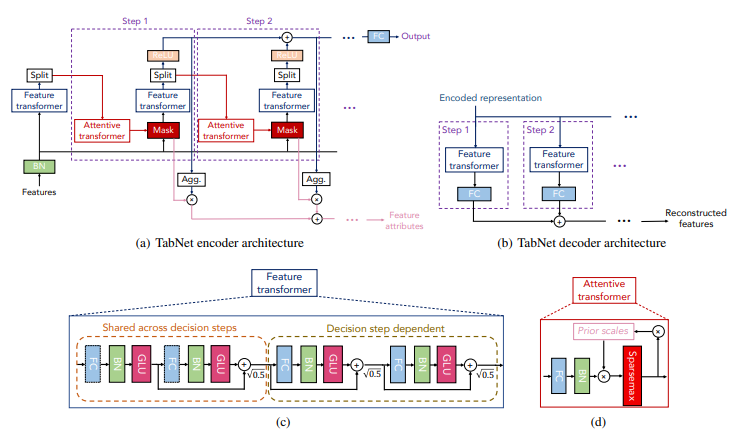
위 그림을 보면 feature transformer를 통해 feature를 preprocessing을 진행하고 decision에 사용할 feature과 다음 step에 필요한 정보를 전달하고 attentive transformer는 주어진 정보를 가지고 masking을 선택 한다.
각 step마다 feature을 선택하고 이를 feature transformer를 통해 decision에 사용할 feature 정보를 ReLU를 통과시키고 합쳐서 점점 쌓는 식으로 representation을 구성한다.
이러한 구조는 Decision Tree의 구조와 같다.(특정 feature를 선택해서 processing하는 것을 통한 hyper plane 형성)
Abstract
tabular domain의 deep learning architecture이고
Decision Tree의 feature selection을 attention으로 구현을 해서 만들었다.
이를 통하 high-performance와 interpretable을 얻었다고 한다.
또한 self-supervised learning 방법도 제시한다.
Introduction
deep learning은 audio, image, text 등에서 representation을 잘 담아내는 식으로 성공적으로 작동을 하였다.
그런데 tabular에는 그럴듯한 성과를 보여주지 못하였다.
tabular에는 딥러닝 대신 decision tree의 앙상블이 지배적으로 사용이 된다.
왜냐하면
- tabular에서 공통적으로 나오는 hyperplane boundary를 표현하기 효과적이기 때문
- decision tree의 구조는 내무 조건을 알 수 있기에 interpretable하다.
- 학습이 빠르다.
논문의 저자는 기존의 DNN의 구조가 tabular data에 적합하지 않다고 한다. (CNN이나 MLP를 그냥 쌓는데 overparametrized되기 쉽기 때문)
즉 tabular에는 적절한 inductive bias가 없기 때문에 optimal solution을 찾기 쉽지 않다.
이 논문은 TabNet을 제시한다.
- TabNet은 preprocessing이 필요가 없고 바로 raw tabular data를 gradient descent로 학습한다.
- 각 feature를 고를 때 sequential attention을 사용한다. 이를 통해 interpretability를 얻을 수 있고 학습에 사용되는 능력이 특정 feature에 집중되기 때문에 더 잘 학습할 수 있다고 한다. 이러한 과정은 data sample마다 따로 진행이 된다고 한다. 그렇기에 각 data마다 다른 feature이 골라질 수 있다.
- 위와 같은 디자인은 2가지 중요한 요소를 보여준다.
- TabNet이 regression이든 classification이든 다른 tabular learning model보다 outperform하거나 동등한 성능을 보여준다.
- 2가지 해석 가능성을 보여준다.
각 sample에 대한 local interpretability: 각 feature이 얼마나 중요한지 알 수 있다.
전체 dataset에 대한 global interpretability: 전체 dataset에서 각 특징이 얼마나 기여하는지 알 수 있다.
- unsupervised pre training을 통해 처음으로 상당한 성능향상을 보였다고 한다.
TabNet for Tabular Learning
DNN을 잘 쌓으면 decision Tree와 비슷하게 output manifold를 구성할 수 있다.
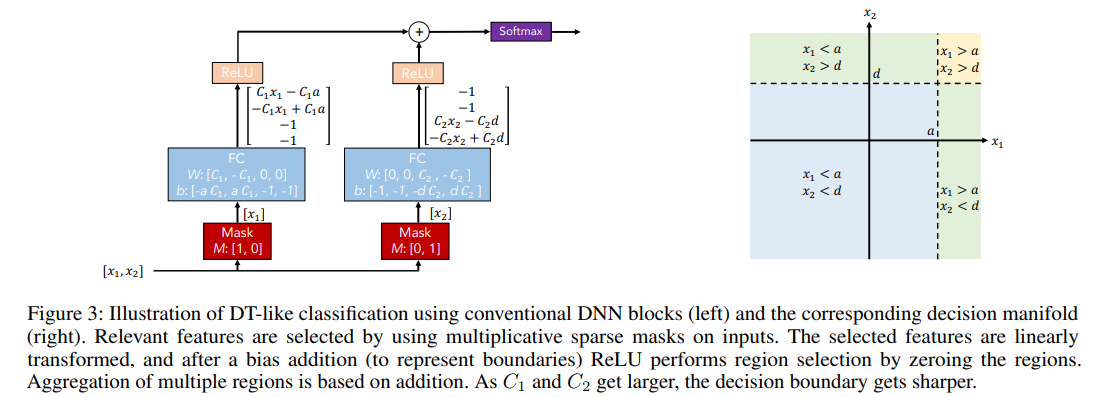 위 그림을 보면 Mask로 각 input을 독립적으로 받은 후 의도적으로 weight를 조절해서 특정 기준선을 정하고 이를 ReLU로 죽이거나 살릴 수 있게 만들었다.
위 그림을 보면 Mask로 각 input을 독립적으로 받은 후 의도적으로 weight를 조절해서 특정 기준선을 정하고 이를 ReLU로 죽이거나 살릴 수 있게 만들었다.
- x1>a, x2>d이면 0번과 3번의 index만 사용하고 나머지는 0
- x1<a, x2>d이면 1번과 3번의 index만 사용하고 나머지는 0
- x1>a, x2<d이면 0번과 4번의 index만 사용하고 나머지는 0
- x1<a, x2<d이면 1번과 4번의 index만 사용하고 나머지는 0
위와 같이 특정 경계를 바탕으로 manifold 구성이 가능해진다.
이때 각각의 feature의 selection이 decision boundary의 key가 된다.
TabNet은 이러한 구조를 바탕으로 디자인을 만들어 Decision Tree를 outperform한다.
- sparse instance-wise feature selection을 data로부터 학습
- sequential multi-step architecture인데 각 step에서 선택된 feature가 decision의 일정 부분 기여
- 선택된 feature에 non-linear processing을 해서 learning capacity를 증가시켰하고 함.
- higher dim과 more step을 통해 앙상블을 모방
TabNet은
- numerical은 raw로 그대로 사용하고 categorical value는 learnable embedding을 이용해서 mapping
- global feature normalization대신 batch normalization 사용
- feature을 차원 에 할당하는데 는 batch size이고 D는 feature dim이다. 이를 각 decision step에 전달한다.
- decision step은 가 진행이 되며 step에서의 input은 step에서 처리된 정보가 들어온다. 각 step에서 어떤 feature을 사용할지 말지 결정하고 이러한 step이 쌓여 전체적인 representation이 구성된다.
Feature selection(attentive transformer)
중요한 feature의 선택에 learnable mask 를 활용해서 로 사용한다.
mask는 다음과 같이 attentive transformer에서 얻어지는데
이다.
이때 이다. 즉 feature들 사이에서 비율로 attention을 주는 것과 비슷한 구조
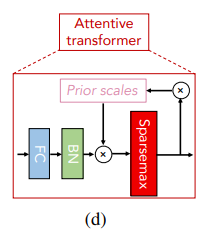
sparsemax는 softmax처럼 크기를 기준으로 나누는 것인데 특정 thershold를 기준으로 나머지를 싹다 0으로 만드는 구조로 softmax인데 0이 많은 버전이라고 생각하면 된다. (정확히는 내림차순으로 정렬하고 로 기준을 나워서 이것보다 작으면 0으로 진행)
softmax는 꼴이라 0이 나올 수가 없다.
수식의 내용을 하나씩 설명하자면 는 나중에 설명할 feature transformer에서 나온 값이고
는 prior scale term으로
로 masking을 조절하는데 만약 이면 각 feature은 오직 1번만 decision step에서 사용된다고 한다.
예를 들어서 일 때 이고 처음 이면 첫번째의 값을 이미 사용하였기에 나중에는 이 되어 나머지 feature은 사용하지 못하는 것과 비슷한 구조
가 1보다 더 크면 여러번 사용할 수 있다.
이다.
추가로 selected feature를 sparse하게 만들기 위해서 entropy regularization을 추가하였다.
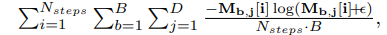 위와 같은데 간단하게 entropy를 미분하면 확률이 분산이 되지 않고 모이게 된다.
위와 같은데 간단하게 entropy를 미분하면 확률이 분산이 되지 않고 모이게 된다.
이 논문에서는 이 entropy regularization이 inductive bias를 추가해준다고 한다. tabular에서는 redundant한 feature이 많기 때문!
Feature processing(featrue transformer)
앞서 부분은 attentive transformer이라면 부분은 Feature transformer의 부분인데
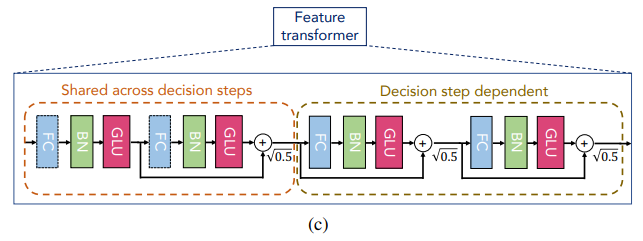 위와 같이 구성이 된다.
위와 같이 구성이 된다.
수식으로는 로 구성이 되고
decision step output 과
information for subsequent step 로 나눠진다.
다양한 테크닉이 들어가는데
- 그림부터 보면 Feature transformer의 layer는 위와 같이 모든 step이 공유하는 layer와 각 step에 독립적인 layer로 구성이 되어있다.
이때 activation으로 GLU가 들어가있는데 GLU는 gated linear unit으로 input으로 들어온 정보를 얼마나 살릴지 정하는 것이라고 보면 된다
보통 아래와 같은 구조이다.여기에서 는 sigmoid이다.
- 그리고 특이한건 residual connetction with normalization인데 찾아보니 Convolutional Sequence to Sequence Learning이라는 논문에서 나온 내용으로 residual에서 로 학습의 안정성을 위해 sum의 variance를 줄였다고 한다.
- ghost batch normalziation을 사용: 찾아보니 큰 batch로 학습할 때 불안정을 줄이기 위해 가상의 virtual batch와 momentum을 이용해서 진행한다고 함. 이때 input feature에는 제외
- section에서 처음 넣은 그림처럼 decision tree와 같은 구조를 사용하기 위해 로 합쳐서 decision output을 구성하고
으로 결과를 예측
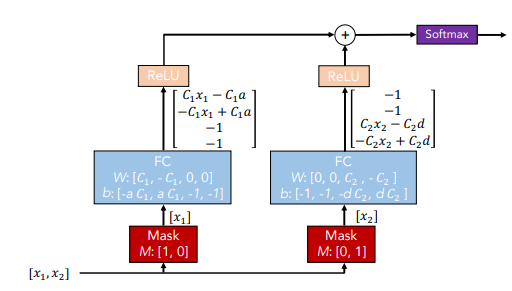
이 그림을 보면 이해하기 쉬울 것 같다. masking을 하고 이렇게 계산한 output을 합쳐서 진행
Interpretability
각 step마다 을 통해서 i번째 step의 batch b의 j번째 column이 미치는 영향을 알 수 있다.
이때 이는 각 단계에 대한 내용이다.
우리는 종합적인 영향력도 보고 싶다. 그러면 각 step의 mask를 weight로 중요도를 따져서 합쳐야 할 것인데 어떻게 할 수 있을까?
이 논문은 로 합쳐진 값을 weight로 활용하였다.
간단하게 설명하자면 각 feature에 대한 decision 값을 전부 합치면 각 step이 미치는 영향력이 나올 것이다. 이를 b번째 sample의 i번째 step에서 결정 기여도로 활용한 것이다.
이를 이용해서 전체 영향력을 볼 수 있는데
이다.
위에서 말한 weight를 곱해주고 전체 step에 대해서 더하는데 이를 전체 feature에 대한 합으로 나눠줘서 feature 전체 합을 1로 맞춰준 것이다.
 이와 같이 전체 attention과 각 step에 대한 attention을 시각화 할 수 있다.
이와 같이 전체 attention과 각 step에 대한 attention을 시각화 할 수 있다.
Tabular self-supervised learning
Self supervised learning을 위한 decoder의 구조도 제시하였다.
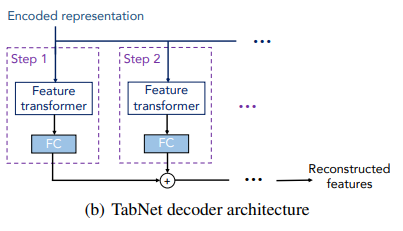 그냥 encoded된 representation을 reconstruct하는 것인다.
그냥 encoded된 representation을 reconstruct하는 것인다.
feature tranfsormer와 FC를 통과한 값들의 합을 이용해서 진행한다.
pretext task로 missing column의 값을 예측하는 것을 제시한다.
binary mask 를 사용하여 encoder의 input으로 를 넣고 decoder의 목표는 를 재구성하는 것이다.
그리고 로 두어서 알려진 특성에만 집중하도록 한다.
decoder의 경우 FC layer의 값과 가 곱해져서 unknown feature의 값에 집중하도록 한다.
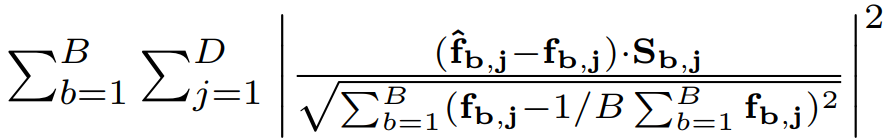 reconstruction loss는 위와 같다. 재밌는건 분모는 batch의 표준편차로 나눠주는데 이렇게 해주는 것은 각 특성이 다른 범위를 가질 수 있기 때문에 도움이 된다고 한다.
reconstruction loss는 위와 같다. 재밌는건 분모는 batch의 표준편차로 나눠주는데 이렇게 해주는 것은 각 특성이 다른 범위를 가질 수 있기 때문에 도움이 된다고 한다.
Experience
test 시에 categorical input은 single-dim learnable scalar을 사용하고 numerical은 그대로 사용하였다.
classification은 cross entropy, regression은 mse를 사용
hyperparam은 validation set으로 최적화
Instance-wise feature selection
특정 subset이 output을 determine하는 dataset으로 feature selection 실험
table output인데 Syn1~3는 모든 instance에서 output과 연관된 featrue가 고정
Syn 4~6은 각 data마다 중요한 feature가 다르다.
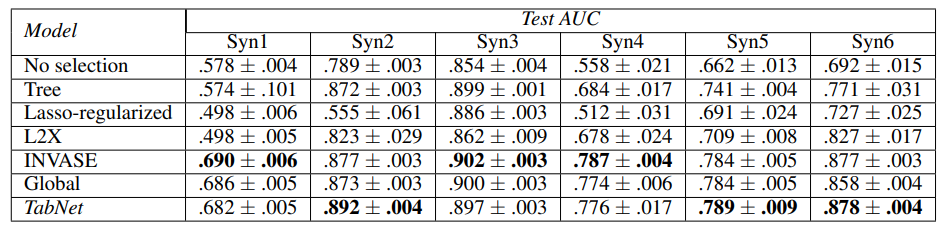 여기에서 Global은 전체적으로 중요한 featrue만 사용한 것이고 No selection은 모든 feature을 사용한 DNN model이다.
여기에서 Global은 전체적으로 중요한 featrue만 사용한 것이고 No selection은 모든 feature을 사용한 DNN model이다.
Syn1~3에서 TabNet이 Global과 비슷한 결과거나 더 좋은 경우를 보여줌. 즉 globally하게 어떤 feature이 중요한지 알아낼 수 있다.
Syn4~6에서 TabNet은 data단위로 필요없는 feature를 걸러낼 수 있는 모습을 보여준다.
그리고 위 dataset에서 TabNet은 중요한 feature이 무엇인지 알아낼 수 있다.
 batch에서 각 step마다 중요한 feature을 보면 Syn2는 output에 중요한 feature()에 집중이 되어있고 Syn4의 경우 각 feature마다 중요한 부분이 다르다.(or )
batch에서 각 step마다 중요한 feature을 보면 Syn2는 output에 중요한 feature()에 집중이 되어있고 Syn4의 경우 각 feature마다 중요한 부분이 다르다.(or )
Performance on real-world datasets
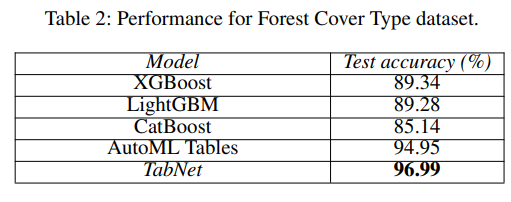
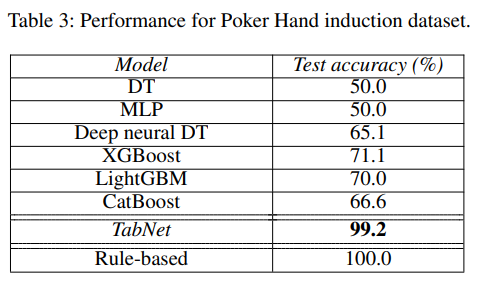
다양한 dataset에서
TabNet이 다른 model을 outperform한다.
Self-supervised learning
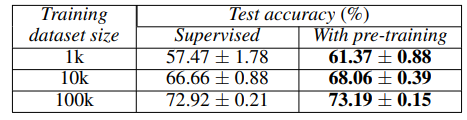 Self-supervised learning을 진행한 이후 학습한 것이 더 성능이 잘 나왔다.
Self-supervised learning을 진행한 이후 학습한 것이 더 성능이 잘 나왔다.
특히 data의 숫자가 적을수록 성능 향상의 폭이 컸다.
