[논문 리뷰 및 구현]Learning Latent Dynamics for Planning from Pixels

pyross·2024년 9월 28일

Mbrl 강화학습 구현 논문리뷰

paper

목록 보기

35/63

논문링크

설명에서 $q$ 는 encoder이고 $p$ 는 model이다.

Abstract

planning은 known environment dynamics의 control task에서 성공을 거두었지만 잘 모르는 환경에서 planning을 위해서 dynamic을 학습하기는 어렵다.
이 논문은 이를 해결하기 위해 PlaNet을 제시한다.
PlaNet은 기존의 dynamic model을 학습하기 어려웠던 image-based domain에서 latent space에서 빠르게 online planning을 하는 방식으로 action을 선택할 수 있다.
좋은 정확도를 얻기 위해서 dynamics model은 몇 step 이후의 reward를 정확히 예측할 수 있어야 한다. 이를 latent dynamics model을 deterministic and stochastic transition component로 해결하였다고 한다.

추가로 이 논문은 multi-step variational inference objective를 제시하였다.
(overshooting)

1. Introduction

잘 모르는 환경에서 plan을 하기 위해서는 experience에서 dynamics를 학습해야 한다.
plan을 할 수 있을정도로 정확한 model을 학습하는 것은 매우 어려운 도전과제이다.

model의 부정확성
multi-step간에 쌓이는 error
다양한 미래를 capture하지 못함
training 분포 밖에서의 overconfident prediction

등이 문제이다.

이 논문은 high-dim environment에서 compact latent 차원에서 dynamic을 학습하여 fast planning을 가능하게 만들었다.

dynamic을 학습하기 위해서 transition model을 stochastic, deterministic component을 결합해서 Recurrent state space model을 만들었다.
게다가 새로운 generalized variational object는 multi-step prediction을 가능하게 만들었다.

논문이 기여한부분은 다음과 같다.

Planning in latent spaces: latenr에서 planning 시행
Recurrent state space model: deterministic, stochastic을 결합. 좋은 성능을 보임
Latent overshooting: long term prediction을 imporve함.

2. Latent Space Planning

unknown environment에서 dynamics를 학습하기 위해서 Planet은 planning을 이용해서 데이터를 모으고 dynamic model을 tranining하는 과정을 반복하였다.

이 절에서는 이미 학습된 dynamic model이 있다고 가정하고 planning을 하는 방법을 소개한다. model의 학습은 3절에서 다룬다.

Problem setup

문제는 partially observable MDP(POMDP)로 가정하고 진행한다.
discrete time step $t$ , hidden state $s_t$ , image observation $o_t$ , continuous action vector $a_t$ , scalar reward $r_t$ , 이후 stochastic dynamics 이고 fixed initial state $s_0$ 으로 구성이 된다.
목적은 policy $p(a_t|o_{\le t}, a_{\lt t})$ 를 $E_p[\sum^T_{t=1}r_t]$ 를 maximize하게 만드는 것이다.

Model-based planning

PlaNet은 이전의 경험으로부터 tradition model, observation model, reward model을 학습한다.

tradition model: $p(s_t|s_{t-1},a_{t-1})$
observation model: $p(o_t|s_t)$
reward model: $p(r_t|s_t)$

dynamic model은 italic이고 true dynamic은 upright letter이다.

여기에서 observation model은 실제 planning에서는 사용되지 않는다.
또한 filtering을 사용해서 과거 이력으로부터 hidden state를 잘 근사하기 위해서 encoder $q(s_t|o_{t_\le t},a_{\lt t})$ 도 학습을 한다.

이런 상황에서 policy는 best sequence를 찾는 action을 planning해서 실행한다.

Model predictive control (MPC) 이고 각 action을 진행한 후 다시 planning을 한다.

MPC를 사용하기 때문에 policy나 value network를 사용하지 않았다고 한다.
(그냥 앞의 상황을 직접 model을 이용해서 해보고 가장 reward가 좋은 action을 고르면 되기 때문)

Experience collection

POMDP이기 때문에 agent가 모든 상황을 다 가보지 못하였기에 반복적으로 experience를 모으고 dynamics model을 학습해야 한다.
그렇기에 위과 같은 구조로 진행이 된다.
model을 학습하고 모델을 이용해서 data를 모으고 다시 학습하고 ...

Planning algorithm

cross entropy method(CEM)을 사용하였다고 하는데 아래와 같다.

간단하게 설명하자면 action의 sequence의 초기에는 Normal(0, I)로 랜덤하게 잡고
action의 sequence를 sampling해서 J개 뽑은 다음 각 action sequence에 따른 state를 뽑는다.
이후 각 state에 따른 reward model이 존재하기 때문에 이를 이용해서 전체 reward를 계산할 수 있다.
여기에서 가장 합이 높은 K개의 action sequence가 있을 것인데
이를 이용해서 K개의 action sequence의 평균과 표준편차를 구할 수 있고
이 평균과 표준편차로 action sequence의 분포를 update한다.

이후 다시 action sequence를 sapling하고 reward가 높은 것을 뽑고 평균과 표준편차를 구하고.. 반복
이 과정은 model을 이용하기에 policy나 value network가 필요가 없다.
쉽게 설명하자면 자연선택을 이용한 진화 기법 같은 업데이트 이다.

저자가 이 알고리즘을 고른 이유는 CEM이 robust하고 true dynamics가 주어지면 모든 task를 풀 수 있기 때문이라고 한다.

3. Recurrent State Space Model

앞서 언급되었다 시피 1번의 step을 위해서 수천번의 action을 평가해야한다.
그래서 이 논문의 저자는 recurrent state-space model(RSSM)을 사용하였다.

이 모델은 비선형 칼만 필터 또는 순차적 VAE로 생각할 수 있다고 한다.

이전 아키텍쳐와의 비교 대신 저자들은 dynamics model이 미래를 디자인 할 수 있는 2개의 중요한 점을 소개한다.
실험에서 전이모델의 확률적 경로의 결정젖ㄱ 경로 모두가 성공에 필수적임을 보여준다.

이 장에서는 latent state-space model에 대해서 상기시키고 RSSM을 소개한다.

Latent dynamics

sequence $\{o_t, a_t, r_t\}^T_{t=1}$ 에서 discrete time step $t$ , image observation $o_t$ , continuous action vector $a_t$ , scalar reward $r_t$ 가 있다고 해보자.

이전의 typical latent state space model은 generative process를 정의하는데
image와 rewrad를 hidden state sequence $\{s_t\}^T_{t=1}$ 에서 생성한다.
왜 stochastic일까
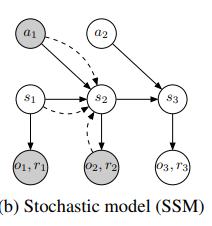
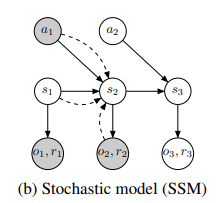
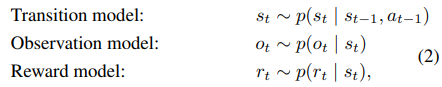transition, observation, reward가 확률적으로 VAE와 같은 구조로 생성되기 때문이다.

transition model은 Gaussian mean, variance를 출력하는 feed forward로 구성.
obsetvation model은 Gaussiacn인데 mean이 deconvolutional network에 의해서 parametrized되었고 identity covariance를 가진다.
항등 공분산을 사용하는 이유는 각 pixel이 독립적이고 분산이 1임을 가정한다는 것 같다.

reward model역시 Gaussian인데 mean이 paramererized되어있고 unit variance를 가진다.

Variational encoder

이 부분은 와닿지가 않아서 100% 이해가 되지 않았다.
우선 설명해보자면 model이 non-linear하기 때문에 param학습에 필요한 state-posterior(상태 사후분포)를 직접적으로 계산할 수 없다.

이 부분이 어려웠는데 state posterior은 새로운 경험을 고려해서 어떤 상태에 관해서 확신하는 정도이다.
$q(s_{1:T}|o_{1:T},a_{1:T})$ 는 과거의 관찰과 행동 $o_{1:T},a_{1:T}$ 을 사용해서 상태의 분포를 추정한다. 이때 시간 $T$ 까지 모든 정보를 고려한다.

그런데 encoder는 각 시간 단계별로 조건부 분해해서 근사한다.
이때 가정이 들어가는데 agent가 가지는 현재 상태에 대한 확신이 오직 바로 이전에 관찰한 것과 행동에 의해서 결정이 된다는 것.
$q(s_{1:T}|o_{1:T},a_{1:T})=\prod^T_{t=1}q(s_t|s_{t-1},a_{t-1},o_t)$
즉 위 수식을 보면 현재 상태 $s_t$ 는 이전의 상태 $s_{t-1}$ ,이전 행동 $a_{t-1}$ , 그리고 현재 관찰 $o_t$ 에 의존한다.
이때 각 $q(s_t|s_{t-1},a_{t-1},o_t)$ 는 cnn과 Feed Forward network에 의해서 평균과 분산을 가지는 가우시안 분포로 가정된다.

이렇게 다 보지 않고 부분을 잘라서 보는 것을 filtering이라고 하는 듯 하다. 이는 현재까지의 관찰을 보고 미래를 계획하는 planning에 적합하다.
그런데 처음 위에서 설명한 것과 같이 전체 사후 분포를 다 고려할 수도 있는데 이는 smoothing이라고 하는듯 하다.

Training objective

encoder를 이용해서 data의 log 유사도에 대한 경계를 생성한다. 이 부분에서는 우선 observation에 대해서만 다룬다. reward도 비슷하다.
첫 부분인 $\mathbb{E}_{q(s_t|o_{\le t},a_{\lt t})}[\ln p(o_t|s_t)]$ 는 간단하게 잠재상태 $s_t$ 로부터 현재 관찰 $o_t$ 를 얼마나 잘 예측을 하냐의 함수이다.

$-KL[q(s_t|o_{\le t},a_{\lt t})||p(s_t|s_{t-1},a_{t-1})]$ 이 부분은 인코더의 분포 q와 모델의 사전분포 p간의 차이를 측정해서 가깝게 만든다.
즉 이전의 모든 분포를 사용해서 예측한 것과 직전의 정보만 사용해서 예측한 것의 차이를 줄임.

Deterministic path

앞서 다룬 모델은 SSM state space model에 다룬 것으로 일반성을 가져서 좋지만 순수한 확률적 transition은 그 확률성 때문에 multiple step을 진행하면 transition model이 정보를 기억하기 어렵게 만든다.

이론적으로 분산을 0으로 만들어서 확률적으로 진행할 수 있지만 optimizer는 이를 찾기 힘들수 있다.

이에 따라서 deterministic sequence를 넣는데 $\{h_t\}^T_{t=1}$ 으로 vector로 구성이 된다. 이에 따라 모델은 그냥 마지막 이전 상태 뿐만 아니라 이전의 모든 상태의 정보를 안정적으로 참조할 수 있다.

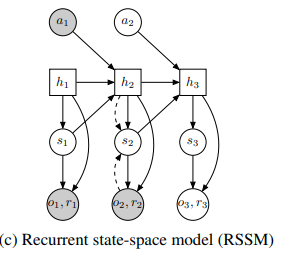
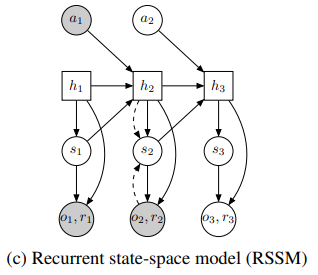
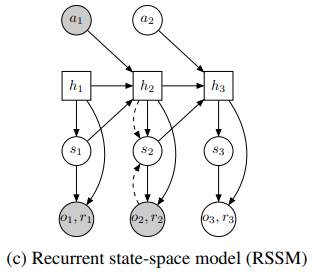
위와 같은 구조로 논문의 저자는 이를 recurrent state-space model(RSSM)이라고 정의하였다.

각각 deterministic, stochastic과 Recurrent의 구조인데
네모는 deterministic, 동그라미는 stochastic이다.
deterministic의 단점은
1. 다양한 future를 탐색하기 힘들고
2. 모델이 부정확한 정보에 확신을 가질 수 있음.
stochastic의 단점은
1. 여러 step이 진행되며 정보를 기억하기 힘들다.
이를 합쳐서 Recurrent state-space model을 구성
위에서 실선은 generative, 점선은 inference인데

실선은 이제 dreamer 등의 논문에서 생성을 하는 과정이고 점선은 encoder와 같이 기존의 내용을 압축하는 것으로 생각된다.

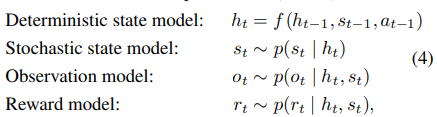RSSM의 구성이다.
위 그림을 보면 쉽게 이해할 수 있다.
이때 encoder는 $q(s_{1:T}|o_{1:T},a_{1:T})=\prod^T_{t=1}q(s_t|h_t,o_t)$ 로 근사를 하여서 확률적인 $s_t$ 의 state posterior를 parameter로 표현하였다.
이때 중요한건 observation에 대한 모든 정보는 encoder의 sampling을 거쳐야 한다.
왜냐하면 reconstruction 과정에서 shortcut을 만들 수 있기 때문(단순히 $o_t$ 를 그대로 사용하는 것이 아니라 $s_t$ 를 제대로 활용하기 위함)

4. Latent Overshooting

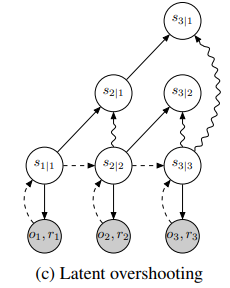
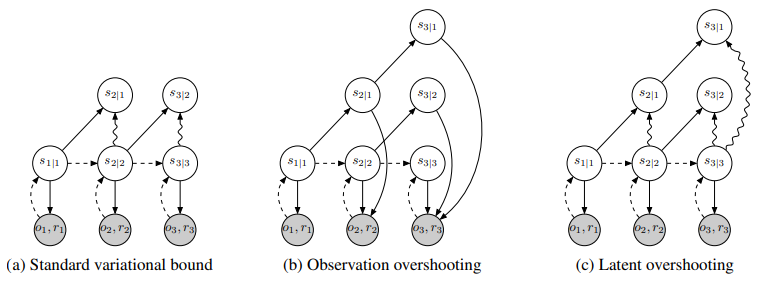위 그림은 학습 과정을 나타낸다.
색칠된 원을 가르키는 arrow는 reconstruction loss term을 나타내고 wave arrow는 KL divergence를 통해 근접시키는 term이다.
(a)는 이전에 위에서 이야기한 보통의 bound인데 설명하자면 $s_{1|1}$ 은 뒤에 의미는 time 1까지의 조건에 따라 앞의 time 1이 생성된 것.
즉 위의 $s_{2|1}$ 은 앞서 $s_{1|1}$ 에서 생성한 것이고 $s_{2|2}$ 는 실제 2까지 조건에 생성된 2니까 posterior term이다.
이에 따라서 각 step마다 $o_t$ 를 reconstruct하는 동시에 이전 분포에서 1번 더 예측한 것과 실제를 KL로 가깝게 만든다.
이 방법의 단점은 multi-step이 아니라 1step이기에 장거리 행동을 학습하기 어렵다.

(b)는 oversation overshooting으로 이전의 state로부터 multiple step이 계속 뻗어 나가고 각 state에서 reconstruction을 진행한다. 이는 multi-step 진행이기 때문에 장거리 행동을 학습할 수 있다고 한다.
그러나 저자는 이런 과정이 비싸다고 한다.

(c)는 저자가 제시한 Latent overshooting이다. 각 state를 실제 posterior와 동일하게 만들어준다.
이는 실제로 몇몇 dynamics model에 효과가 있었다고 한다.

1step도 만약 완벽하게 예측이 가능하다면 multi-step이 필요가 없다고 한다.
그러나 실제 상황에서는 inaccuracy 때문에 1 step도 부정확 해서 planning을 위해서 multi step prediction을 따로 학습을 진행해주었다고 한다.

Multi-step prediction

기존 수식을 변경하는데 simple하게 표현하기 위해서 표기에 action을 제외하였다. $s_t$ 는 $a_{\lt t}$ 에서 나왔다고 생각하면 된다.
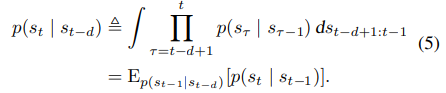위 식에서 d=1이면 기존과 같은 one-step transition이 된다.
식에대한 설명은 일단 t-d부터 t까지 전이를 확률 곱을 진행하였는데 이를 $s_{t-d+1:t-1}$ 로 적분을 하였다
그럼 아래와 같이 확률 $p(s_{t-1}|s_{t-d})$ 에 대한 $p(s_t|s_{t-1})$ 의 평균이 된다.

이러한 식을 토대로 기존식을 multi-step으로 바꾸었다.
위 식은 기존의 수식이다.
$p_d$ 는 multi-step predictive distribution이라고 한다. 앞서 설명했던 것과 같이 action을 simplity를 위해서 지웠기에 달라보이지만 거의 비슷하다.

reconstruction은 사실상 위 그림을 봐도 똑같지만 아래의 multi-step preidction은 바뀌었는데 $p(s_{t-1}|s_{t-d})$ 가 추가 되었고 $q(s_{t-d}|o_{\le t-d})$ 로 바뀌었다.
이 부분이 뜻하는 것은 multi-step predictive distribution을 train할 수 있고 이는 이전의 observation을 보지 않고 예측을 할 수 있다는 것이다.

Latent overshooting

마지막으로 Latent overshooting의 식은 다음과 같다.
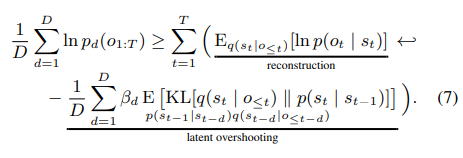D는 distance의 bound이다.
간단하게 아래 그림의 식이다.

$\beta_{\gt 1}$ 를 조절해서 모델이 long-term에 집중할지, short-term에 집중할지 조절할 수 있다.

5. Experiments

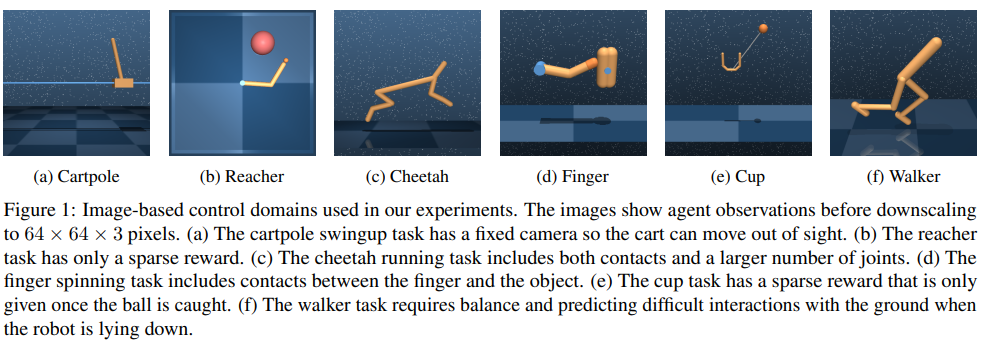
위 6가지를 task로 설정하였는데 특징을 간단히 적자면

cartpole: long planning horizon이 필요. 또한 화면 밖으로 나갔다면 memorize가 필요.
reacher: sparse reward가 hand and goal area가 겹치면 부여
cheetah: larget state and action space
Finger: include contact dynamics
cup: sparse reward
walker: most challenging. robot need to stand up and walk

이때 observation은 64x64x3 pixel
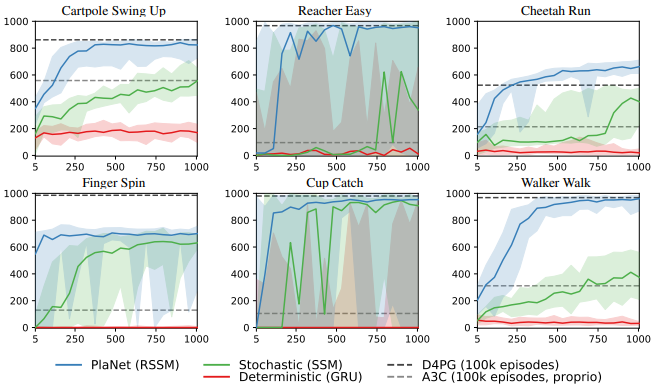다른 방법들과 비교하였을 때 매우 뛰어난 결과를 보임.
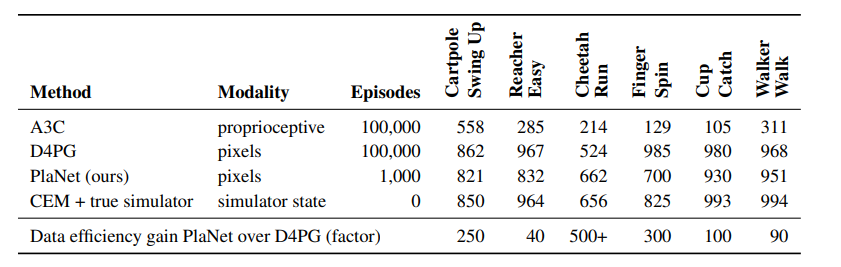이때 mbrl의 장점인 매우적은 episode로 높은 점수 달성

구현

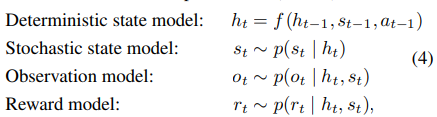
encoder: $q(s_t|h_t,o_t)$

위 내용을 토대로 대강 간단하게 구현해보았다.

deterministic

class DeterministicStateModel(nn.Module):
    def __init__(self, stochastic_dim, action_dim, deterministic_dim, hidden_dim):
        super(DeterministicStateModel, self).__init__()
        self.rnn = nn.RNNCell(stochastic_dim + action_dim, deterministic_dim)
    
    def forward(self, s_prev, a_prev, h_prev):
        x = torch.cat([s_prev, a_prev], dim=-1)
        h = self.rnn(x, h_prev)
        return h

stochastic

class StochasticStateModel(nn.Module):
    def __init__(self, deterministic_dim, stochastic_dim, hidden_dim):
        super(StochasticStateModel, self).__init__()
        self.fc_mu = nn.Linear(deterministic_dim, stochastic_dim)
        self.fc_logvar = nn.Linear(deterministic_dim, stochastic_dim)
    
    def forward(self, h):
        mu = self.fc_mu(h)
        logvar = self.fc_logvar(h)
        std = torch.exp(0.5 * logvar)
        return mu, std

observation, reward는 구현이 동일

class ObservationAndRewardModel(nn.Module):
    def __init__(self, deterministic_dim, stochastic_dim, observation_dim, hidden_dim=256):
        super(ObservationModel, self).__init__()
        self.fc1 = nn.Linear(deterministic_dim + stochastic_dim, hidden_dim)
        self.fc_out = nn.Linear(hidden_dim, observation_dim)
    
    def forward(self, h, s):
        x = torch.cat([h, s], dim=-1)
        x = F.relu(self.fc1(x))
        o_mean = self.fc_out(x)
        o_logvar = torch.zeros_like(o_mean) # 로그 분산이니까 0을 넣으면 1로 취급 0=ln(1)
        return o_mean, o_logvar

Encoder

class Encoder(nn.Module):
    def __init__(self, observation_dim, deterministic_dim, stochastic_dim, hidden_dim):
        super(Encoder, self).__init__()
        self.cnn1 = nn.
        self.fc1 = nn.Linear(observation_dim + deterministic_dim, hidden_dim)
        self.fc_mu = nn.Linear(hidden_dim, stochastic_dim)
        self.fc_var = nn.Linear(hidden_dim, stochastic_dim)
    def forward(self, o, h):
        x = torch.cat([o, h], dim=-1)
        x = F.relu(self.fc1(x))
        mu = self.fc_mu(x)
        var = self.fc_var(x)
        return mu, var

이후 forward
위 그림 굵은 선

    def forward(self, o, a, h_prev, s_prev):
        # Update deterministic state
        h = self.deterministic_model(s_prev, a, h_prev)
        # Encode to get posterior parameters
        mu, std = self.stochastic_model(h)
        # Sample stochastic state using reparameterization
        epsilon = torch.randn_like(std)
        s = mu + epsilon * std
        # Generate observation
        o_mean, o_logvar = self.observation_model(h, s)
        # Generate reward
        r_mean, r_logvar = self.reward_model(h, s)
        return h, s, o_mean, o_logvar, r_mean, r_logvar, mu, std

pyross

AGI

이전 포스트

[논문 리뷰]SubTab: Subsetting Features of Tabular Data for Self-Supervised Representation Learning

다음 포스트