[논문 리뷰]SubTab: Subsetting Features of Tabular Data for Self-Supervised Representation Learning

논문링크

이번 논문은 핵심만 간단하게 적겠다.

Abstract

tabular dataset에 대한 augmentation가 부족함을 알리고 feature의 subset을 이용해 tabular represenation learning을 muti-view representation learning으로 만든 학습 방법을 제시함.

corrupted feature으로부터 원본을 복구하는 것보다 subset을 통해서 복구하는 것이 더 좋다고 주장한다.

1 Introduction

tabular data의 augmentation의 가장 대표적인 방법은 noise를 추가하는 corrupt이다. 이를 autoencoder와 같이 이용해서 원본을 복구하는 작업이 가장 대표적이다.
이를 통해 noise에 robust한 representation을 만들 수 있다.

그러나 이러한 방법은 모든 feature의 정보성을 동등하게 대해서 효과적이지 않고 정보가 없는 feature에 noise를 넣는 것은 원본의 목표(noise에 robust한 representation)을 달성하기 더 어렵게 만든다.
최근 논문들은 tabular의 self-supervised learning을 위해서 corrupted된 feature을 맞추는 등의 pretext task를 디자인하는 경우도 있지만 이 또한 noisy data input에 의존적이고 classifier를 high-dim의 imbalanced binary mask에 학습하는 것은 의미있는 representation을 학습하기 어렵다.

이 논문은 data의 feature을 cropping하는 것처럼 나눠서 multi-view로부터 1개의 representation을 학습하는 앙상블과 같은 문제로 바꾼다.
또한 이러한 방법이 noise를 추가하는 것보다 더 효과적인 representation을 학습하기 쉽다고 주장한다.

2 Method

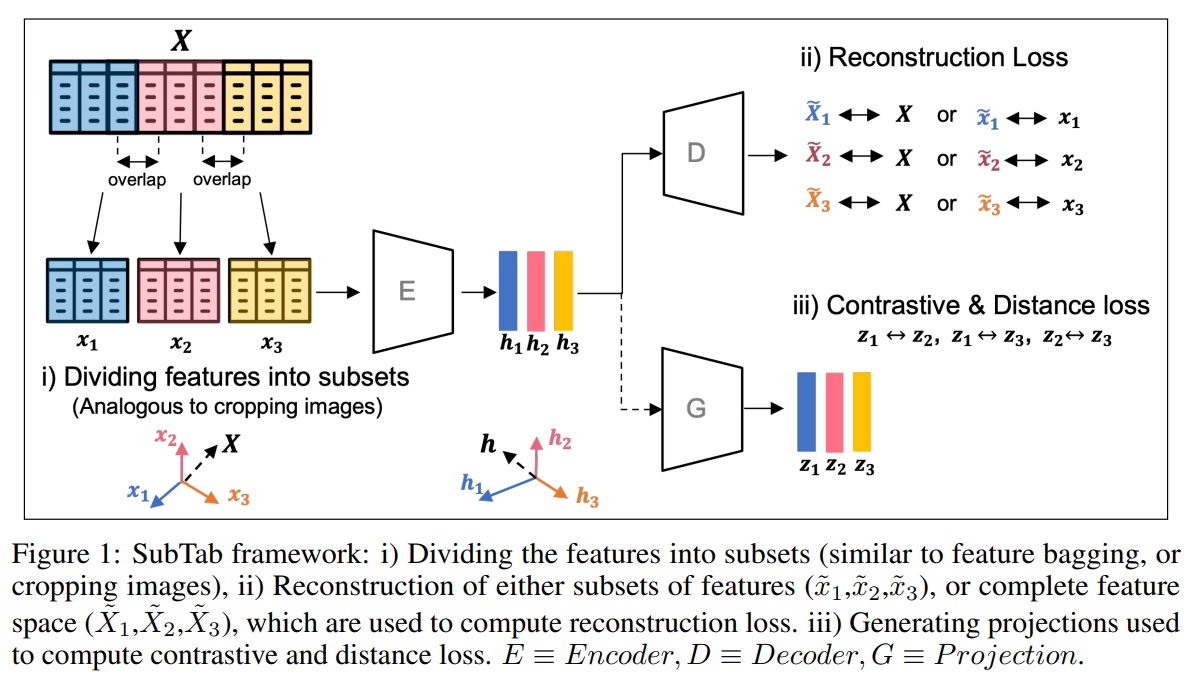구성은 encoder(E), decoder(D), optional projection(G)이다.
h가 representation이고 z가 projection, $\tilde x$가 reconstruction인데 $\tilde x$는 부분이고 $\tilde X$는 전체 이다.

SubTab framework에서는 sliding window로 나누는 것 같다. 인접한 feature은 겹칠 수 있다고 한다. 겹치는 비율은 subset의 percentage를 정해서 나눌 수 있다고 한다.
이러한 subset은 동일한 encoder로 들어가서 각각의 representation이 만들어진 다음 shared decoder에 들어가서 전체를 복구하거나 subset 원본을 복구한다.

이 논문에서는 전체를 복구하는 것을 골랐다. 이게 representation을 학습하기 더 쉽고 identity mapping, 즉 원본을 그대로 복구하는 것이 아니라 입력 부분 집합으로 전체 데이터를 예측하게 하기 때문에 bottleneck의 제약을 없애는 방식으로 학습을 한다.
이러한 loss를 subset마다 구한다.

또한 추가로 2개씩 비교하는 contrastive loss를 추가할 수 있다.
위 예시의 경우 $_3C_2$의 경우로 3개가 가능하다.
그리고 각 사이의 거리를 가깝게 하는 MSE 등의 loss도 추가할 수 있다.
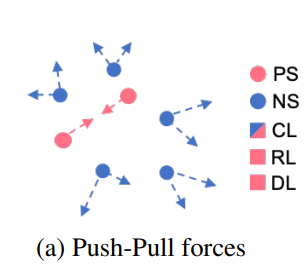contrastive loss는 위와 같이 positive는 가깝게, negative는 멀게 한다.

추가로 feature들 간의 상대적 위치는 고정한다. 왜냐하면 MLP의 경우 위치가 바뀌면 기존에 학습하는 것도 무용지물이 되기 때문.

2.1 Strategies for adding noise

SubTab의 기법은 다른 기법들과 상호 보완적(complementary)이다. 그러니까 대체가 아니라는 의미이다.
그래서 sub feature에 추가로 Noise를 넣는 실험도 해보았다.
Noise는 3가지 종류인데
1. 가우시안 노이즈 (Gaussian Noise): 더해준다.
2. 스왑 노이즈 (Swap-Noise): 다른 sample의 column 값으로 바꾼다.
3. 제로 아웃 노이즈 (Zero-Out Noise): random column의 값을 0으로 바꾼다.

여기에서 Noise를 더하는 방법도 다양하게 하였다.

아래와 같이 Noise를 더한다.
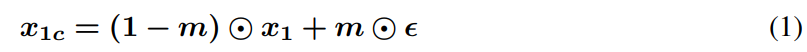m은 binomial matrix이고 $\epsilon$은 noise matrix인데 subset feature의 크기와 동일하다. masking matrix는 확률 p로 0또는 1이 할당된다.

2.2 Training

loss는 위와 같이 구성이 된다.
각각 reconstruction, contrastive, distance loss이다.
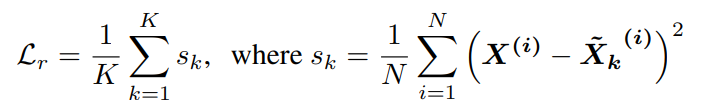reconstruction loss는 위와 같은데
K는 전체 subset의 개수이고 N은 batch의크기이다.
MSE를 모든 subset에 대해서 진행하고 평균을 낸 것이다.

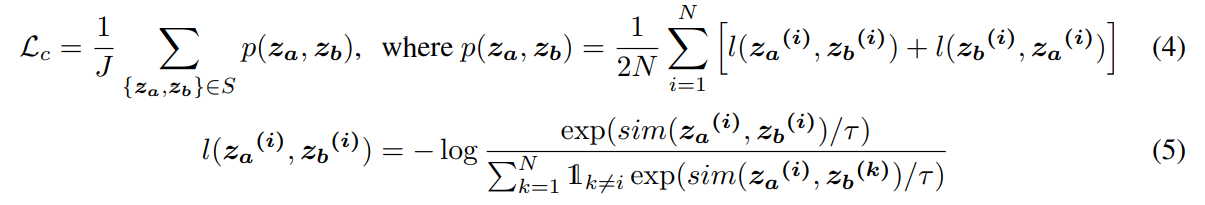
contrastive loss는 위와 같다.
간단하게 J는 모든 set pair의 개수이고 두 set에 대해서 contrastive learning을 진행한다.

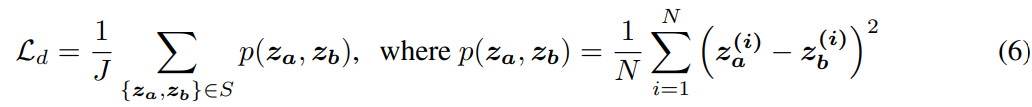
distance loss는 그냥 MSE를 subset에 대해서 한 것이다.

2.3 Test time

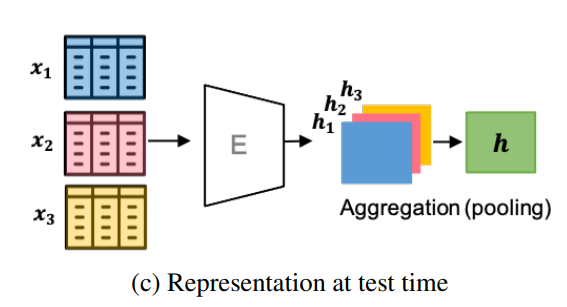
위와 같이 test set에 대해서 training과 같이 subset을 나눈 다음에 Encoding을 진행하고 이를 겹쳐서 pooling을 하여서 사용함.
다양한 방법이 가능하겠지만(Min, Max, mean ...)이 논문에서는 Mean을 사용

실험에서 1개를 사용하거나 subset 몇개를 사용해도 좋은 성능이 나왔다고 함.

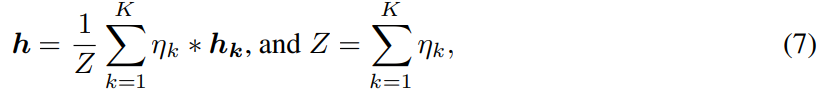
이때 weighted Mean을 위와 같이 구성이 가능한데
$\eta$는 learnable param이다.
또한 위와 비슷하게 1D-CNN을 사용할 수 있다.

3 Experiments

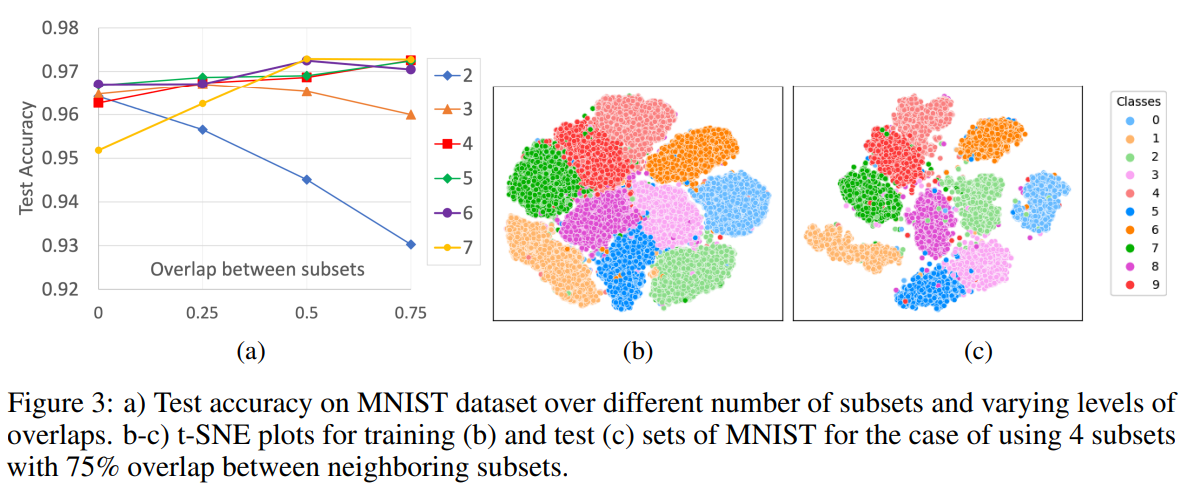위 그림은 noise를 추가하지 않고 flatten해서 학습한 MNIST dataset에 대한 subset size와 overlap 비율에 대한 성능 차이이고 오른쪽은 trarining, test의 t-sne이다.

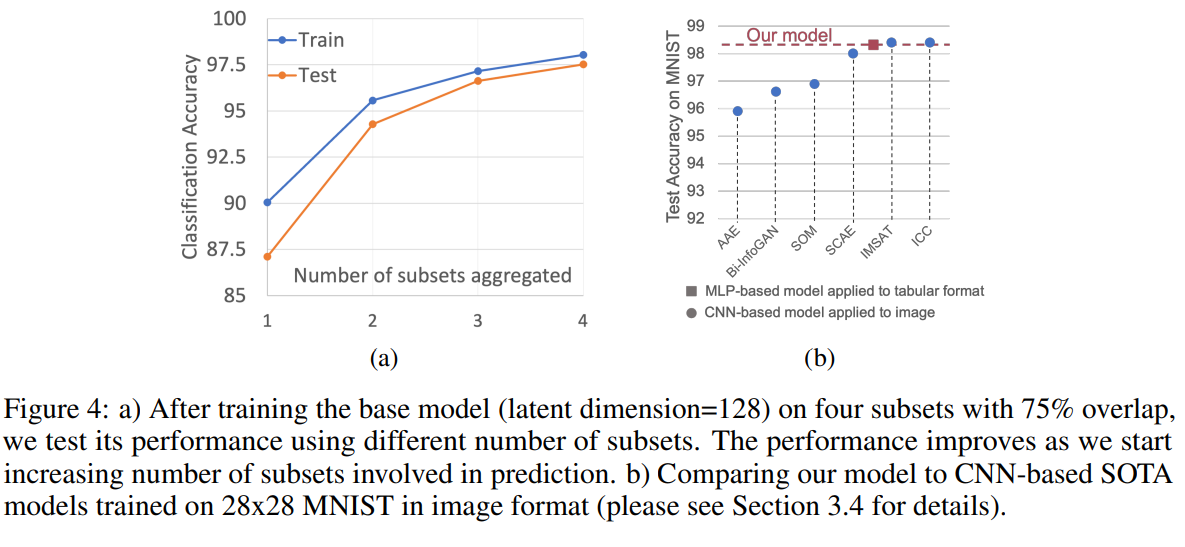위 그래프는 test단계의 subset aggregated의 개수가 많으면 성능이 올라간다는 것을 보여준다.

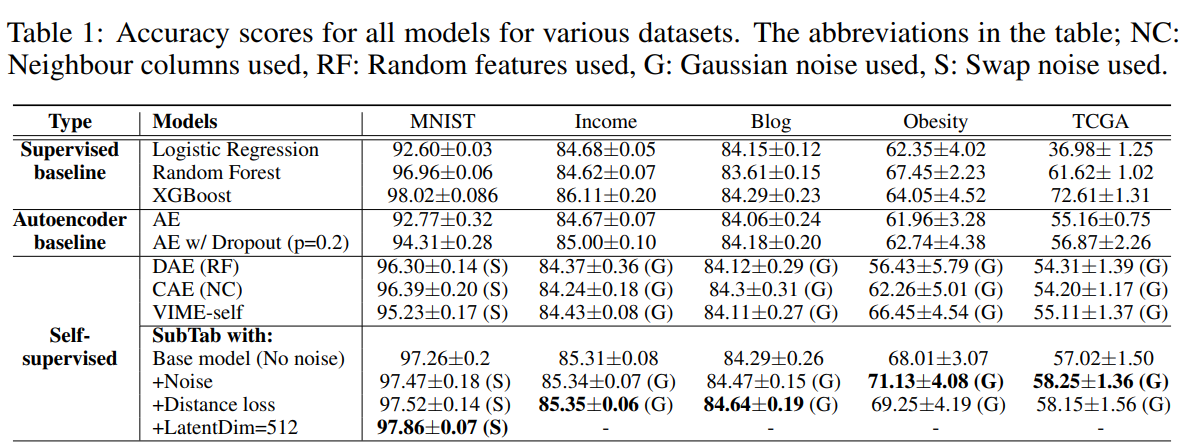다양한 data에서 매우 좋은 성능을 보였다.