요약
Diffusion을 통해서 trajectory를 생성하는 방식으로 planning을 진행하는 매우 획기적인 논문.
전체 trajectory를 diffusion을 통해서 생성해내기에 one-step error이 쌓이는 문제가 사라진다.
또한 reward의 conditional하게 생성을 하는데 reward의 gradient를 이용해서 진행하기에 reward를 바꿔도 gradient만 얻으면 되기 때문에 영향을 받지 않기에 task를 여러가지 진행할 수 있다.
Abstract
model based 강화학습은 종종 dynamic model을 approximate하는 데에만 중점을 두고 나머지 decision making은 기존의 trajectory optimizer에 전부 맡기는 경우가 있다.
이런 조합은 간단하지만 학습된 model이 기존의 trajectory optimization에 잘 맞지 않을 수도 있고 부족한 부분이 많다.
이 논문은 trajectory optimizatoin pipeline을 modeling과 합치는 것을 고려한다. 예를 들어 model에서 sampling하는 것과 planning을 하는 것을 합치는 것처럼.
이를 위해 diffusion 모델을 이용하는데 iterative denosing trajectory를 통해서 planning을 진행한다.
1 Introduction
Abstract에서 언급했듯이 learned model을 이용한 planning은 environment의 dynamics를 supervised와 같이 학습한 model을 이용해서 classic한 trajectory optimization으로 진행하는 경우가 많다.
그러나 이러한 경우 대부분 잘 작동하지 않는다. 왜냐하면 trajectory를 생성해서 진행을 하는 과정에서 optimal trajectory를 찾는 것이 아니라 adversarial example을 찾아 planning을 진행하는 것과 비슷해지기 때문이다.
이 부분에서 advesarial example의 뜻이 내가 생각하기에 adversarial attack처럼 plan을 진행할 때 trajectory를 생성할텐데
사실 model이 완벽한 환경을 구축하기는 어렵고 approximation을 진행하는데 그러다보니 특수한 경우에 매우 뛰어난 것처럼 '보이는' trajectory를 찾게 되는 것을 의미하는 것 같다.
결국 그런 hallucination trajectory를 가지고 plan을 세우면 실제로 잘 작동하지 않기에 optimal trajectory가 아니라는 뜻 같다.
그렇기에 대부분의 mbrl의 추세는 value, policy gradient등을 가져오는 식으로 model-free에서 많이 가져와서 진행한다.
실제로 저번에 공부한 dreamer도 학습한 model을 actor critic과 같은 방법으로 활용한다.
이 논문은 이러한 문제를 해결하기 위해서 sampling과 planning을 동일하게 처리해서 trajectory optimization을 쉽게 처리하는 모델을 학습하는 것을 제시한다.
이를 위해 planning 위주로 design된 모델을 구축하는데
- planning에서 action distribution이 state dynamics만큼 중요하고
- long-horizon accuracy가 single-step accuracy보다 중요하다.
- 여러 task에서 적용이 되어야 하기 때문에 특정 reward function에 종속이 되어서 진행이 되면 안된다.
- 마지막으로 prediction이 아니라 plan을 위한 모델이 되어야 하기에 경험을 통해서 개선이 되고 myopic failure 즉 장기적으로 보지 않고 근시안적으로 진행해서 실패를 하는 것에 취약하면 안된다.
이 논문은 위 문제들을 trajectory-level diffusion 확률 모델로 시작한다.
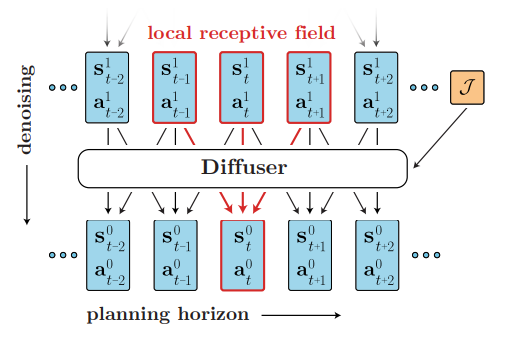
기존의 model-based planning이 autoregressively 즉 하나씩 예측하며 진행이 되었다면 Diffuser는 모든 timestep plan을 한번에 예측한다.
Diffusion model의 iterative sampling은 flexible한 conditioning을 가능하게 하고 guide의 활용을 가능하게 한다.
다음의 장점이 있다.
- Long-horizon scalability: Diffuser은 1 step의 예측이 아니라 전체 trajectory의 예측에 더 중점을 두기 때문에 rollout을 통해서 점점 step이 진행되며 error이 쌓이는 문제를 완화한다. 그렇기에 더욱 scalability하다.
- Task compositionality: reward function이 auxiliary gradient로 활용이 되기 때문에 reward function을 바꾸면 다른 task를 사용할 수 있기에 다양한 task에 활용할 수 있고 그 gradient를 다 더해주면 여러개의 reward를 구성할 수 있다.
- Temporal compositionality: diffuser은 1d cnn으로 진행을 하기 때문에 local consistency를 유지하면서 improve가 진행이 된다.
위 그림을 보면 과거와 미래를 토대로 현재의 state를 업데이트 하기에 시간적인 일관성이 유지가 된다. - Effective non-greedy planning: model과 planner의 차이를 줄임으로써 model의 prediction을 개선하는 것이 곧 planning 능력의 개선을 하는 것이다.
디퓨전에 아직 친숙하지 않아서 내용이 조금 어려웠는데 알고보니 간단한 원리였다.
state와 action을 1D vector이라고 보고 concat을 한 다음. diffusion을 통해서 horizon만큼 modeling을 진행하는데 reward의 gradient를 토대로 최적의 원본 x를 modeling을 하는 식으로 진행하게 되면 이게 곧 planning이 된다.
3 Planning with Diffusion
핵심은 위에서 설명한 것과 같다.
이때 diffusion의 trajectory가 일때 history에 대한 확률, goal에 대한 확률, optimize를 위한 general function 등을 라고 할때
를 통해서 생성되는 trajectory를 최적화 하는 것이 곧 planning이 된다.
3.1 A Generative Model for Trajectory Planning
diffusion을 통해서 얻는 이점이 있는데
- Temporal ordering: 이전에는 로 진행이 되었다면 이제는 로 미래의 관점까지 고려할 수 있기 때문에 현재의 선택이 과거에 의해서 선택될 뿐만 아니라 미래의 결과까지 고려한 일관적인 state를 얻을 수 있다.
- Temporal locality: 위처럼 앞 뒤 맥락을 고려하면 이미지에서 주변 픽셀을 고려하는 convoluation처럼 locality를 따질 수 있다. 그렇기에 일관성을 유지
- Trajectory representation: 이와 같이 state와 action을 concat한 상태로 (horizon, state)와 같이 된 input을 처리할 수 있어야 한다.
이 논문은 위 모든 내용을 만족시키기 위해서 1D conv를 이용한 U-Net과 같은 구조를 사용하였다.
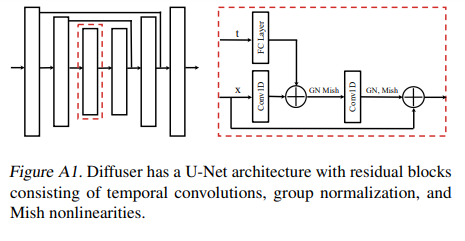
학습은 DDPM과 동일하게 noise를 예측.
DDPM을 잘 모르면 논문리뷰를 보고 오자.
3.2 Reinforcement Learning as Guided Sampling
reward term에 대한 내용인데 한가지 예시를 보여준다.
만약 가 binary random variable이라면 즉, 각 time step이 optimal인지 아닌지 보여주는 것이라면 trajectory에 대한 확률을 구할 수 있을 것이고
로 설정할 수 있다.
그렇기에 로 표현할 수 있다.
즉 샘플을 생성해서 를 최대화하는 것이 아니라 가 최대화가 된 샘플을 생성하는 문제로 바꿀 수 있다.
즉 위에서 reward function 에 대한 최적의 샘플을 생성하면 그것이 최적의 planning일 것이다!
그리고 이는 conditional sampling으로 볼 수 있다.
이때 가 smooth하면 gaussian으로 reverse diffusion process를 근사할 수 있다고 한다.
위처럼 두 조건에 따른 결과를 오른쪽과 같이 근사할 수 있고
이때 와 은 의 원본의 평균과 분산이다.
이때 는 reward의 미분 값인데 다음과 같이 표현이 가능하다. 간단하게 현재 구성이 된 원본 trajectory에서 최적의 가 나올 log 확률의 gradient이다.
위와 같으며 이를 늘린다는 것은 를 증가시키는 것이다.
이때 diffusion 와 reward model 를 독립적으로 학습을 시켜서 diffusion과 reward가 다르기에 reward만 바꾸면 다른 task를 진행하는 모델을 만들 수 있다.
는 cumulative reward를 학습한다고 한다.
내용이 매우 어려워서 나도 이해하기 힘들었는데 의사 코드를 같이 보면서 이해해보자.
위와 같은 상황이다.
처음에 initial state 에서 시작한 상황이라고 할 때 임의의 trajectory를 생성하는 과정이다.
3번째 줄은 초기 gaussian noise를 설정하는 부분이고 4번째는 Diffusion의 denoising step의 수이다.
6번째 줄은 원본의 를 예측한다. 즉 현재 step단계에서 예측한 최종 경로의 평균을 만들어낸다.
8번째 줄은 그렇게 만든 경로 mu에 reward의 gradient를 더해주고 sampling을 진행하는데 이게 뭐냐면 최종 trajectory를 gradient가 증가하는 방향으로 수정하는 것이다.
즉 최종적으로 reward가 증가하는 trajectory를 생성하기 위한 planning을 한 것이다!
이후 10번째 줄에서는 초기 state를 initial state 로 설정해서 초기 state를 설정해준다.
이후 첫번째 state의 action을 실행한다.
위 내용인데 간단하게 최적의 trajectory를 diffusion과 gradient ascent를 이용해서 생성하는 것이다!
3.3 Goal-Conditioned RL as Inpainting
앞에서 우리가 한 planning은 reward를 최대화 하는 것인데 특정 planning은 특정 location에 들어가거나 특정 state가 되는 등의 constraint satisfaction인 경우가 있다.
이런 경우 문제를 inpaining problem으로 볼 수 있다.
즉 이미지같은 경우 특정 부분이 주어지고 나머지를 생성하는 것이다.
Diffusion을 통해서 특정 action, state 만 채워두고 나머지를 생성하면 해결된다.
위 알고리즘의 경우 처음 state를 제한한 것처럼 특정 state 부분을 결과 state로 덮어씌우고 생성을 진행하는 것이다.
5 Experimental Evaluation
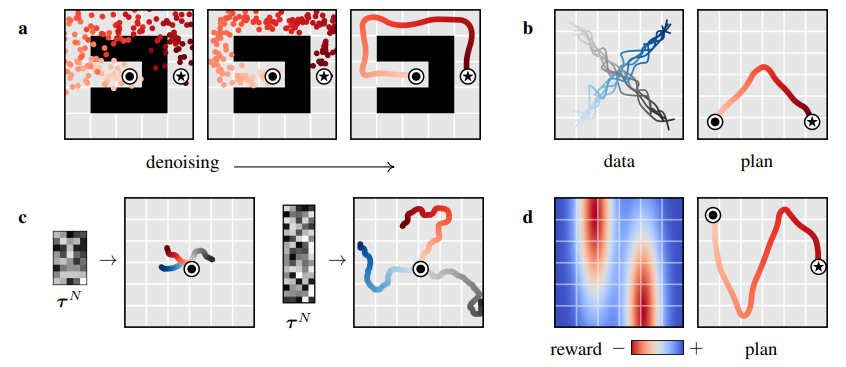 위 그림처럼 noise의 크기를 바꾸는 등 유동적인 planning이 가능하고 denoising을 통한 long horizon planning이 가능하다.
위 그림처럼 noise의 크기를 바꾸는 등 유동적인 planning이 가능하고 denoising을 통한 long horizon planning이 가능하다.
또한 reward에 따른 planning이 이루어진다.
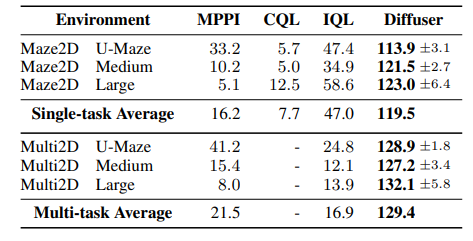
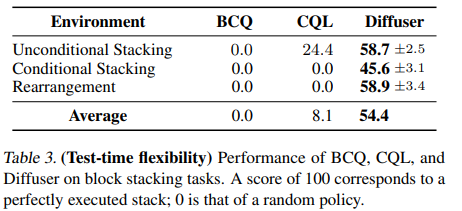
또한 다른 모델에 비해서 sparse reward, long horizon 상황인 maze에서 뛰어난 결과를 얻음.
test time에서 diffusion model은 그대로 두고 reward가 바뀌는 경우를 테스트 해도 역시 잘했다.