[논문 리뷰]Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model

논문링크

요약

알파고 제로는 MCTS를 이용해서 기존에 게임 rule 즉 dynamics가 주어진 상황에서 진행이 되었지만 MuZero는 dynamics가 주어지지 않고 이를 학습한 모델을 가지고 진행을 하는
즉 model based reinforcement learning으로 진행을 한다.

짧게 요약하자면
representation function을 통해 이전의 observation 들을 가지고 root hidden state를 만들고 dynamics function을 통해 특정 action을 하였을 때의 다음 hidden state를 구하고 각 state를 에서 prediction function을 통해 value, policy를 예측하고 MCTS를 진행한다.
이후 구한 MCTS 값을 이용해서 점점 오차를 줄이고 강화하는 식으로 학습이 진행된다.

Abstract

이전에 알파고와 알파고 제로 등 MCTS를 이용해서 매우 좋은 성능을 보였는데 하지만 이때 dynamics를 주어진 상태로 진행을 하였다.
그러나 실제 환경에서는 환경의 dynamics가 주어지지 않거나 complex한 경우가 매우 많다.
그렇기에 이 논문은 MuZero를 제시하는데 이는 사람의 데이터 뿐만 아니라 환경에 대한 정보도 주어지지 않고 Tree 기반 학습을 진행하는 방식으로 SOTA의 성능을 달성했다.

1 Introduction

기존 Planning으로 좋은 성능을 얻은 방법들은 게임 규칙 등 dynamics를 알도 있는 상태에서 진행을 하였다. 그러나 실제로는 환경의 dynamics를 모르는 경우가 더 많다.

그렇기에 MBRL을 진행하는데 MBRL은 우선 환경을 학습한 모델을 구축하고 이를 토대로 planning을 진행한다. 이때 모델은 environment state나 observation sequence를 reconstruction하는 식으로 진행이 된다.

하지만 model 방법은 atari 등 visually rich domain에서 성능이 매우 떨어졌고 model free 방법이 SOTA였다. 그러나 model free는 체스, 바둑 등 planning이 필요한 부분에서 약하다.

이 논문은 MuZero를 제시하는데 이는 model-based RL 방법론이고 기존의 체스, 바둑 뿐만 아니라 아타리에서 SOTA를 달성을 하였다.

구성은 다음과 같다.

• model이 observation을 받으면 hidden state로 변환
• hidden state는 이전 hidden state와 action을 가지고 recurrent 하게 업데이트
• 각 step마다 policy, value, reward를 예측

위처럼 구성이 되는데 재밌는 부분은 hidden state를 활용 함으로써 model이 original observation을 reconstruct할 필요가 없기에 더 필요한 정보를 담을 수 있다.

이러한 특성은 PlaNet 논문에서도 활용이 되었다.

3 MuZero Algorithm

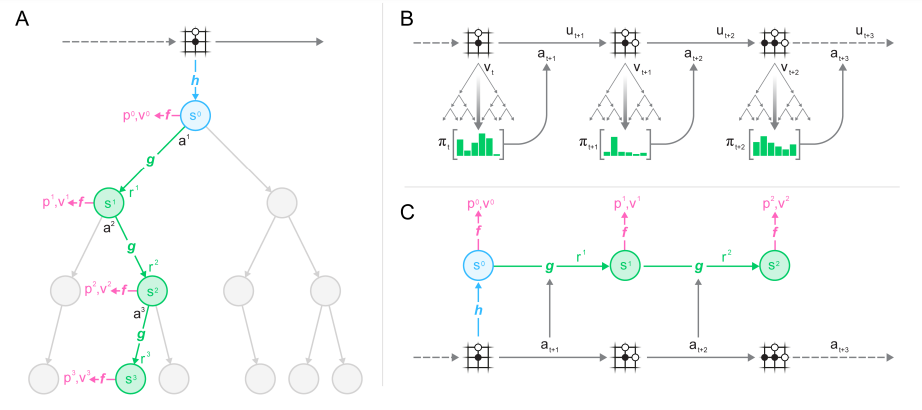위 그림으로 요약된다.

기존 model based 강화학습처럼 policy, value, reward를 이용하는게 핵심이다.

각 time step t에서 k step 만큼 진행이 되며 모델은 representation, dynamic, prediction 3가지의 조합으로 진행이 된다.
진행 방법은 다음과 같다.

• representation function이 과거의 observation을 encode한다. $s^0=h_\theta(o_1,...,o_t)$
• dynamics function이 임의의 action을 따라서 다음 state와 reard를 진행 $r^k,s^k=g_\theta(s^{k-1},a^k)$ 이때 이전의 mbrl과는 다르게 hidden state에는 observation에 대한 정보 위주가 아니라 미래의 값을 예측하기 위한정보가 주로 담긴다.
• prediction function을 통해 값을 예측한다. $\bm p^k,v^k=f_\theta(s^k)$로 이전 알파고 제로와 동일.

이 상황에서 알파고 제로와 동일하게 MCTS를 policy $\pi_t$와 value $v_t$를 만들고 $a_{t+1}\sim \pi_t$를 만들어서 이를 토대로 진행한다.

학습은 모든 policy, value, reward를 각 step마다 예측된 값과 실제 값을 맞추는 식으로 진행을 한다. 알파제로와 메우 비슷하다.

• policy의 경우 현재 $\bm p^k_t$와 search를 통해 찾은 $\pi_{t+k}$의 error를 줄인다.
• value의 경우에도 알파 제로와 비슷하게 게임을 진행하고 예측하는 식으로 진행이 된다. 그러나 마지막 결과 reward만 고려하던 알파제로와는 다르게 범용성을 위해서 discounting과 intermediate reward를 사용하는 경우도 고려하였다.
  아타리의 경우 $z_t=u_{t+1}+\gamma u_{t+2}+...+ \gamma^{n-1}u_{t+n}+\gamma^n v_{t+n}$이고
  보드 게임의 경우 마지막 결과 {lose, draw, win}={-1,0,+1}로 설정이 되었다.
• value도 $v^k_t$와 $z_{t+k}$의 차이를 줄이도록 학습되었고
• reward는 observed reward와 예측 reward를 줄이도록 학습이 되었다.

시간 t에서의 전체 loss는 다음과 같다.
$l_t(\theta)=\sum^K_{k=0}l^r(u_{t+k},r^k_t)+l^v(z_{t+k},v^k_t)+l^p(\pi_{t+k},\bm p^k_t)+c||\theta||^2$
마지막은 l2 regularization이다.

4 Results

$K=5$로 학습이 되었다. 즉 t=0부터 5step을 고려
representation function은 AlphaZero와 동일하게 conv, residual로 구성하는데 이전에는 20 block였는데 16 block으로 줄였다.
dynamic function과 prediction function도 이와 동일하게 구성.

위 그림이 결과인데 보드게임에서 알파제로의 결과는 오렌지 색이고 뮤제로는 파란색이다.
아타리의 경우 이전 model free SOTA 모델인 R2D2의 결과가 오렌지색이다. 실선은 평균, 점선은 중간값.
SOTA의 뛰어난 점수를 보여준다.

그런데 조금 걸리는 내용이 학습할 때 staet $s_t$에 대한 term이 없다.
state를 가지고 예측한 policy, value, reward를 학습하는 식으로 간접적으로 진행이 되는데 그러면 초기 representation $s_0$을 가지고 dynamic을 통해 예측한 $s_1$과 실제 환경에서 다음 step을 진행하고 다시 만든 representation $s'_0$과 조금 다른 의미를 가질 수 있는데 그러게 된다면 학습이 너무 복잡하게 될 것 같다.
실제로 PlaNet의 경우 예측한 state와 실제 다음 state를 KL로 가깝게 하는데 그러한 term이 없는것이 조금 걸린다.