논문 링크
ICML2024 best paper이다.
역시 읽었지만 사실 기존에 공부하던 내용이 아니라서 100% 이해하기는 어려웠는데 이해한 내용만 간략하게 작성해보겠다.
요약
간단하게 요약하자면 SMC sequential monte carlo로 각 단계별 목표 분포를 맞추면서 진행하는데 마지막은 target distribution으로 정해서 target 분포에서 샘플링을 하는 것이 목표이다.
target 분포는 RLHF, toxic generation, reward model의 분포 등 목표하고 있는 분포 생각하면 될 것 같다.
1. Introduction
최근 model의 output을 steering하는 것이 중요한데 RLHF 등으로 조절한다.
그런데 중요한 부분은 이러한 target 분포가 unnormalized 되어 있고 보통 전체 sequence를 평가하는 방식이기에 그 분포에서 sampling하기 매우매우 어렵다.
이때 target 분포를 다음과 같이 확률로 표현이 가능한데
σ(s1:T∣s0):=Zσ(s0)1p0(s1:T∣s0)ϕ(s1:T)
이때 s0는 prompt, s1:T는 각 token sequence, σ는 target 분포이고 p0는 LLM의 분포로 생각하면 되고
ϕ(s1:T)는 sequence를 평가하는 unormalized density 즉, reward 값이라고 생각하면 된다.
그리고 Z는
Zσ(s0)=s1:T∑σ~(s1:T∣s0)=s1:T∑p0(s1:T∣s0)ϕ(s1:T)
로 확률 분포로 만들어주는 가능한 모든 값들의 합으로 수 있다.
그냥 간단하게 target 분포는 생성하는 분포(llm)*target density 값 의 normalized로 볼 수 있다.
그러면 저 target 분포에서 바로 뽑을 수 있다면 엄청 좋은거 아닐까?
말이 쉽지 사실 어렵다.
가능한 모든 경우의 수를 따져야해서 Zσ를 구하기 사실상 불가능하기 때문이기도 하고 LLM의 경우 sequence를 순차적으로 생성하기 때문에 다 생성하고 평가를 해야하기 때문이다.
하지만 중간 단계에서 평가할 수 있으면 어떨까?
σ(s1:t)=∑st+1:Tσ(s1:T)=p0(s1:t)∑st+1:Tp0(st+1:T∣s1:t)ϕ(s1:T)/Z
을 만족하기에 만약 우리가 marginal분포 그러니까 가능한 모든 경우의 숫자를 다 고려해서 ϕ를 다 계산해줄 수 있으면 t step에서의 target 분포, σ(s1:t)를 구할 수 있을 것이다.
하지만 이것 역시 불가능하기 때문에 ψt(s1:t)≈∑st+1:Tp0(st+1:T∣s1:t)ϕ(s1:T)으로 근사를 하는데 ψ는 neural network로 학습을 해서 근사한다.
그러니까 강화학습에서의 value function과 같은 기능을 할 수 있게 하는 것이다.
결국 introduction에서 좀 많은 이야기를 했는데 핵심은 ψt(s1:t)로 미래에 가능한 ϕ의 분포 근사하는 value function과 같은 기능을 할 수 있게 근사하는 것이다.
2. background
이 논문은 잘 모르는 용어가 많이 나와서 background가 매우매우 중요한데 자세하게 설명하겠다.
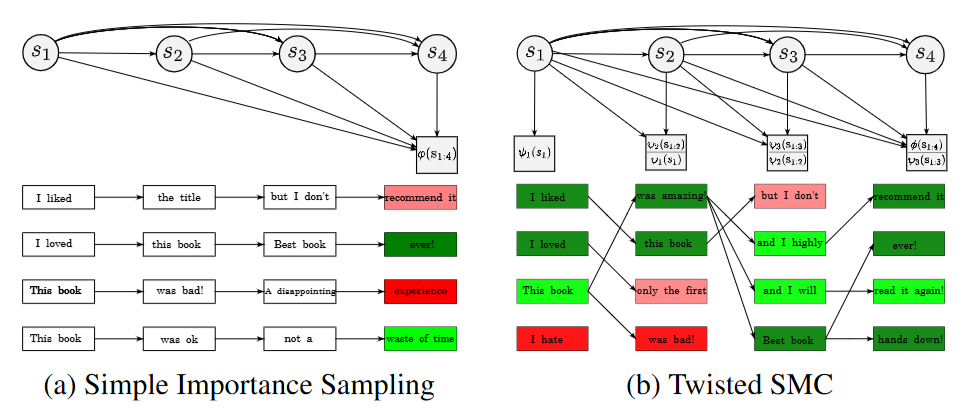
2.1. Simple Importance Sampling
important sampling은 다들 알 것이다. 만약 x를 q분포에서 추출해서 f(x)의 평균을 계산한다고 하면 평균은 ∑xq(x)f(x)=Eq(x)[f(x)]일 것인데 만약 q분포에서 sampling하기 힘드니까 p(x)p(x)q(x)로 p(x)p(x)=1이니까 이 분포를 곱해줘서 뽑기 쉬운 분포로 바꿔주는 것이다.
그럼 Ep(x)[p(x)q(x)f(x)]가 되는데 이때 p(x)q(x)=w로 weight가 된다.
weight의 직관적인 뜻은 q(x)의 확률은 높은데 현재 뽑은 p(x)의 확률이 낮으면 가중치를 매우 크게 줘서 값을 보정하는 것이고 반대로 q(x)의 확률이 낮은데 p(x)가 높으면 값을 줄여서 보정한다.
이게 끝이다.
이 논문은 설명할 때 Zσ를 구하는 것이 중요한데
Zσ=∑s1:Tσ~(s1:T)인데 이를 important sampling으로 q 분포에서 뽑는다고 하자
그럼 weight는 특정 sequence s1:Ti에 대해서 w(s1:Ti):=q(s1:Ti)σ~(s1:Ti)가 될 것이다.
이 값을 넣어주면 Zσ=∑s1:Tq(s1:T)q(s1:Ti)σ~(s1:T)=Eq(st:T)[w(s1:T)]가 될 것이고
즉, Z^σSIS=K1∑i=1Kw(s1:Ti),s1:Ti∼q(s1:T)로 근사치를 구할 수 있다.
이는 unbiased estimator이다.
여기에서 다시 중요한 부분이 나오는데 우리가 K개의 sample을 뽑으면 이제 앞의 공식을 활용해 식을 정리할 수 있는데
Eσ(s1:T)[f(s1:T)]=∑s1:Tσ(s1:T)f(s1:T)=∑s1:TZσσ~(s1:T)f(s1:T)
여기에서 q에서 K개의 sample을 뽑아서 근사하면 다음과 같이 나온다.
Eσ(s1:T)[f(s1:T)]≈∑k=1K∑j=1Kw(s1:Tj)w(s1:Tk)f(s1:Tk)
위 식이 나오는 이유는 self normalized importance weight을 찾아보면 이해하기 쉬울 것 같다.
직관적으로는 아래 부분은 Z^σSIS이고 위 부분은 wegiht의 정의에 따라서 σ~(s1:T)=q(s1:T)w(s1:T)이기 때문에 s1:T∼q(s1:T)에서 윗 부분의 q가 상쇄되고 w만 남고Z^σSIS는 위 식에 따라서 대입하면 된다.
여기에서 저 식을 다시 보면 ∑j=1Kw(s1:Tj)w(s1:Tk)의 분포가 σ(s1:T)와 비슷하게 근사가 된다는 것을 알 수 있다.
이를 이용해서
s1:Tσ←s1:Tw,w∼cat({∑j=1Kw(s1:Tj)w(s1:Tk)}i=1K)로 resampling하는 과정으로 볼 수 있다.
이부분이 잘 이해가 안갈 수 있는데 K개의 sample을 구하고 각각 정의에 따라서 weght를 측정한다.
이후 그 weight를 가지고 각 weight/전체 weght의 합으로 분포를 구해서 index를 sampling해서 resampling하면 weight가 큰 sample은 여러번 나올 것이고 weight가 작은 sample은 숫자가 줄어들 것이다.
이렇게 다시 K개의 sample을 재구성 하면 그 분포가 σ에서 뽑은 것과 비슷해진다는 것이다.
간단하게 sampling->weight측정->index resampling하면 그 분포가 target에 맞게 바뀐다는 것이다.
2.2. Sequential Monte Carlo
앞에서 important sampling시에는 sequnce가 s1:T로 모든 time step이 다 주어져있다고 생각을 했다. 그러나 LLM과 같은 경우 s1:t와 같이 중간 step도 존재한다.
이와 비슷하게 sequential monte carlo는 중간 time step t의 분포를 따로 만들어서 target의 분포가 서서히 변하게 만드는 것이다.
{π~t(s1:t)}t=1T로 중간 unnormalized intermediate target distribution을 설정한다.
이때 중요한 것은 πT(s1:T)=σ(s1:T)로 설정하면 중간 step이 어떻든 간에 마지막 step에서 target distribution으로 수렴한다는 것이다.
이때 weght의 설정이 중요하다 wt(s1:t)=π~t−1(s1:t−1)q(st∣s1:t−1)π~t(s1:t)로 설정한다.
이렇게 설정하는 이유는 t step의 target 분포가 π~t−1(s1:t−1)π~t(s1:t)으로 설정되기 때문이다.
q는 proposal로 위에서 말한 sampling하기 쉬운 분포이고 π~t−1(s1:t)이 곱해지는 이유는 직관적으로 이전 step에서 target이 잘 맞춰졌다면 distribution이 π~t−1(s1:t)일 것이기 때문에 이를 상쇄시키고 다음 distribution으로 넘어가기 위함이다.
weight를 위와 같이 설정하면 이전 2.1에서 배운대로 resampling을 통해서 target 분포에 맞추면서 step을 진행할 수 있다.
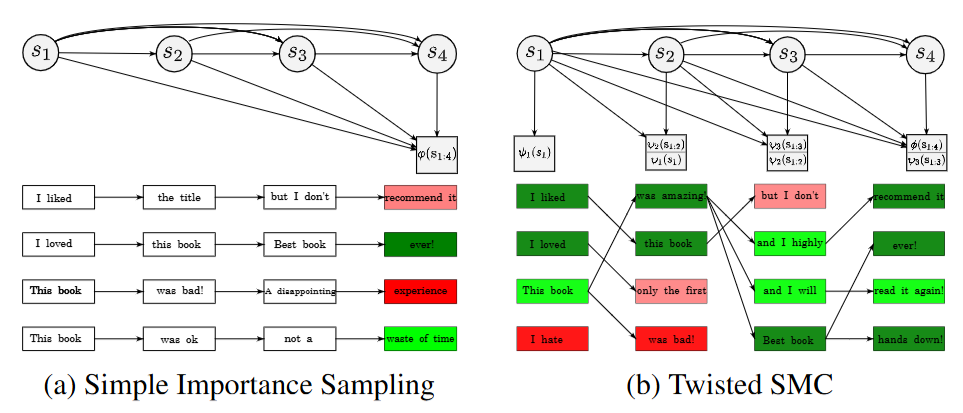
간단하게 t-1 step이라고 할때 t step token sampling -> weight 측정-> resampling으로 target 분포 맞추기 이후 반복...
위 그림처럼 진행이 된다.
결국 마지막의 분포가 σ이기 때문에 점점 σ의 분포로 수렴하게 되는 것이다.
3. Twisted Sequential Monte Carlo for Language Modeling
앞에서 대부분 필요한 내용을 다 설명하였기에 간단하게 설명하겠다.
우선 ψt(s1:t)≈∑st+1:Tp0(st+1:T∣s1:t)ϕ(s1:T)으로 미래의 reward를 marginal하게 근사된 함수가 있다고 하자.
그러면 우리는 중간 step의 target을 다음과 같이 설정할 수 있다.
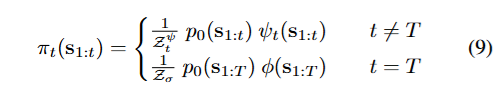
이를 이전에 설정했던 weight wt(s1:t)=π~t−1(s1:t−1)q(st∣s1:t−1)π~t(s1:t)에 넣으면 다음처럼 구성이 되는데
wt(s1:T)=q(st∣s1:t−1)p0(st∣s1:t−1)ψt−1(s1:t−1)ψt(s1:t)
이를 활용해서 wegiht를 구할 수 있고 resampling을 통해서 target density에 맞는 분포로 sampling할 수 있다.
이게 이 논문의 핵심이다.
논문에 제시된 proposal을 어떻게 설정하는지는 따로 다루지 않겠다.
강화학습과의 연관성은 그냥 ψt가 미래에 대한 reward를 고려하는 것이기에 value function으로 볼 수 있다는 내용이다.
4. Learning the Twist Functions
그러면 어떻게 저 ψt를 학습할 수 있을까?
4.1. Contrastive Twist Learning
가장 직관적인 방법은 간단하게 KL term으로 학습하는 것이다.
θminLCTL(θ)=θmin∑t=1TDKL(σ(s1:t)∣∣πtθ(s1:t))
이때의 gradient는
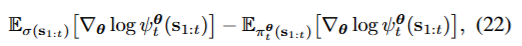 이렇게 나오는데 이렇게 나오는 이유는
이렇게 나오는데 이렇게 나오는 이유는
πtθ(s1:t)=∑s1:tp0(s1:tψtθ(s1:t))p0(s1:t)ψtθ(s1:t)를 미분하기에 저렇게 나온다.
앞은 분자인 positive term 즉, σ(s1:t)에서 뽑은 분포이기에 증가시키고
뒤는 분모인 negative term 즉, 가능한 모든 경우를 뽑기에 감소시키는 모양이다.
위 두 식을 학습하기 위해서는 positive term과 negative term을 학습해야 하기 때문에 positive sample과 negative sample을 구해야 한다.
4.1.1. APPROXIMATE NEGATIVE SAMPLING
negative sample을 구하는 법은 간단하다 그냥 앞에서 하던대로 πt를 목표로 뽑으면 된다.
4.1.2. (APPROXIMATE) POSITIVE SAMPLING
positive target 즉, σ(s1:t)에서는 어떻게 뽑을까?
Exact Target Samples
이 부분은 잘 이해하기 못했는데 BDMC trick 즉, 계속 샘플링하고 평가하는 과정을 통해서 target 분포에 맞는 sample을 이용해서 진행하는 것으로 보였다.
Rejection Sampling
rejction sampling은 likelihood ratio q(s1:T)σ~(s1:T)≤M을 이용해서 진행한다.
대충 설명하자면 target 분포가 f(x), proposal이 g(x)라고 할때 Mg(x)를 활용해서 Mg(x)f(x)의 값을 비교해서 uniform distribiton의 값이 그 값보다 작으면 포함되게 진행하는 것이다. 그럼 target distribution에서 뽑은 것과 비슷한 효과가 나온다.
이때 target σ~(s1:T)가 특정 조건을 만족하면 1이되는 indicator와 곱해져서 p0(s1:T)∗indicator(1or0)로 구성이 되거나 classifier 등, joint distibution p0(s1:T)σ(oT∣s1:T)로 구성이 되면 proposal 분포 q가 p0면 ≤M=1이 항상 성립하기에 쉽게 기준을 세워서 rejection sampling을 할 수 있다.
간단하게 설명하자면 positive와 비슷한 것을 남기고 버린다.
Approximate Positive Sampling using SIS or SMC
앞에서 important sampling을 진행했을 때 마지막에 resampling을 진행하면 그게 target distribution을 근사하기에
그 normalized weight를 이용하면 positive term의 first term 즉, expected gradient를 측정할 수 있다고 한다.
이 부분도 잘 이해하지 못했는데 SIS나 SMC를 마지막 step에서 진행하면 결국 target distribution을 근사해서 뽑는 것과 비슷한 효과를 보이기에 그 weight를 이용해서 학습하는 것으로 보인다.
Truncation to Partial Sequences
exact positive sample을 뽑았다면 이를 자른 partial sequence를 timestep t에서의 positive sample로 볼 수 있다.
이를 통해서 gradient를 업데이트한다.
5. Evaluating Inference in Language Models
대강 설명하겠다.
앞에서 우리는 Z^σSIS=K1∑i=1Kw(s1:Ti),s1:Ti∼q(s1:T) 등으로 Zσ의 근사치를 구하는 법을 배웠다.
그럼 이를 이용해서 그 lowerbound와 upperbound를 구할 수 있고 이를 이용해서 품질의 평가가 가능하다는 이야기이다.
DKL(q(s1:T)∣∣σ(s1:T))=Eq[logp0(s1:T)ϕ(s1:T)q(s1:T)]+logZσ
DKL(σ(s1:T)∣∣q(s1:T))=Eσ[logq(s1:T)p0(s1:T)ϕ(s1:T)]−logZσ
를 만족하는데
그 이유는 KL term에 σ(s1:T∣s0):=Zσ(s0)1p0(s1:T∣s0)ϕ(s1:T)를 넣으면 바로 나온다.
위 수식을 정리하면
Eq[logq(s1:T)p0(s1:T)ϕ(s1:T)]=logZσ−DKL(q(s1:T)∣∣σ(s1:T))이고
Eσ[logq(s1:T)p0(s1:T)ϕ(s1:T)]=logZσ+DKL(σ(s1:T)∣∣q(s1:T))이라서
Eq[logq(s1:T)p0(s1:T)ϕ(s1:T)]≤logZσ≤Eσ[logq(s1:T)p0(s1:T)ϕ(s1:T)]를 만족한다.
KL term은 0보다 크니까
이를 논문에서는
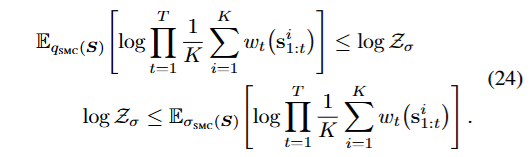 이와 같이 표현을 하였다.
이와 같이 표현을 하였다.
이 두 lower와 upper의 차이를 통해서 얼마나 logZσ를 잘 근사하고 σ의 분포에서 잘 뽑아내느냐를 평가할 수 있다고 한다.

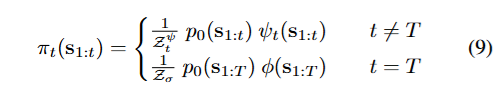
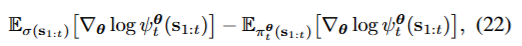 이렇게 나오는데 이렇게 나오는 이유는
이렇게 나오는데 이렇게 나오는 이유는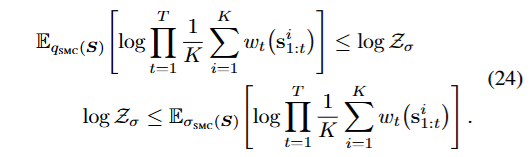 이와 같이 표현을 하였다.
이와 같이 표현을 하였다.