논문링크
요약
PPO의 이전에 나온 논문이고 매우 유명하고 매우 어려운 논문이다.
주제는 monotonic improvement를 보장하는 방법이 없을까?이다.
이를 위해서
η(π~)=η(π)+Es0,a0,⋯∼π~[∑t=0∞γtAπ(st,at)](1)에서 시작해서
Lπ(π~)=η(π)+∑sρπ(s)∑aπ~(a∣s)Aπ(s,a).(3)로 1차미분을 통한 근사를 진행하고
이때 근사를 얼마나 해야할지 lower bound를 구해서
η(π~)≥Lπ(π~)−CDKLmax(π,π~),where C=(1−γ)24ϵγ(9)이렇게 식을 구성한다.
이 lower bound를 상승시키면 monotonic improvement가 보장이 된다.
그러나 실제로 적용하기 어렵기에 이를 타협해서 constraint로 penalty를 보내고 advantage를 Q로 변경하고 importance sampling등의 기법으로 sum을 expectation으로 수정한 다음
maximizeθsubject toEs∼ρθold,a∼q[q(a∣s)πθ(a∣s)Qθold(s,a)](14)Es∼ρθold[DKL(πθold(⋅∣s)∥πθ(⋅∣s))]≤δ.
이렇게 수식을 구성해서 실제 학습을 진행한다.
TRPO는 성능이 잘 나온다기 보다는 이렇게 하였을 때도 학습이 된다는 내용이고 추후 나온 PPO의 배경이기에 중요하다.
Abstract
이 논문은 policy를 optimize하는 과정에서 monotonic improvement를 보장하는 방법을 설명한다.
이는 TRPO(Trust Region Policy Optimization)으로 이론적 정의된 내용을 근사하는 방법으로 학습이 이루어진다.
다양한 task에서 robust한 성능을 얻었다고 한다.
1 Introduction
이 논문은 대체 목표 함수(surogate objective function)을 최적화하는 것이 policy 개선을 보장한다는 것을 증명하고 시작한다.
이후 이론적으로 정의된 알고리즘을 approximation하는 것으로 실제 적용을 한다.
이게 TRPO이다.
이 TRPO는 2개의 variant가 존재하는데
- single-path method: model-free 환경에서 사용 가능
- vine method: 시스템을 특정 상태로 복구가 가능한 시뮬레이션 같은 상황에서 사용이 가능하다.
이러한 TRPO를 통해 복잡한 문제를 풀 수있었다고 한다.
2 Preliminaries
명명법으로 시작한다. MDP 환경이 (S,A,P,r,p0,γ)로 구성이 될때
S:finite set of states
A: finite set of actions
P:S×A×S→R으로 구성이 된 transition 확률
r:S→R인 reward 함수
p0:S→R인 initial state s0의 확률
γ∈(0,1) discount factor이다.
π:S×A→[0,1]로 stochastic policy이고
η(π)=Es0,a0,...[∑t=0∞γtr(st)]로 expected discounted reward 이다.
이때 s0∼p0(s0),at∼π(at∣st),st+1∼P(st+1∣st,at)이다.
또한
Qπ(st,at)=Est+1,at+1,…[∑l=0∞γlr(st+l)]
Vπ(st)=Eat,st+1,…[∑l=0∞γlr(st+l)]
Aπ(s,a)=Qπ(s,a)−Vπ(s),whereat∼π(at∣st),st+1∼P(st+1∣st,at)for t≥0
을 만족한다.
그냥 전체 notation은 간단하게 MDP 환경이고 Q는 action value, V는 value, A는 advantage이다.
여기에서 재밌는 부분이 나온다.
우리가 다른 policy π~의 expected return을 구하기 위해서 현재 알고있는 policy π를 이용할 수 있는데
η(π~)=η(π)+Es0,a0,⋯∼π~[∑t=0∞γtAπ(st,at)](1)
위와 같은 식으로 구할 수 있다.
식의 의미는 π~의 expected return은 policy π의 expected return에 π~의 trajectory에서 policy π의 advantage를 더해준 것이다.
이 부분이 사실 와닿지 않았는데
정책 π의 advantage Eat∼π(at∣st)[Aπ(st,at)]=0인 것을 생각하면 이해가 조금 쉽고
advantage는 그 행동 자체의 value라고 생각하면 더 와닿는 것 같다.
예를 들어서
만약 state가 s0,s1, action은 a0,a1만 있는 상황에서 초기 state는 s0이고 무슨 짓을 하든 s1으로 가고
R(s0,a0)=1이고 R(s0,a1)=0이라고 하자.
이때 policy가 π는 π(a0∣s0)=0.5,π(a1∣s0)=0.5일때
policy π의 기대보상은 0.5이다. state 0에서 1×0.5+0×0.5이기 때문.
이때 advantage는 Aπ(s0,a0)=1−0.5=0.5, Aπ(s0,a1)=0−0.5=−0.5이다.
이제 π~를 생각해보자 π~(a0∣s0)=0.7,π~(a1∣s0)=0.3일때
π~의 expected return은 0.7이다.
이를 위 수식을 통해 구하면
η(π~)=η(π)+0.7×0.5+0.3×−0.5=0.5+0.35−0.15=0.7로 정확한 값이 구해진다.
π~의 확률 분포와 π의 advantage 즉 행동을 하였을 때 얻는 return의 기댓값과 곱해져서 차이를 만들어내고 이 차이를 원래 policy π의 기댓값과 더해져서 π~의 기댓값으로 만들어지는 것이다.
- 추가로 위 식의 증명은 다음과 같다.
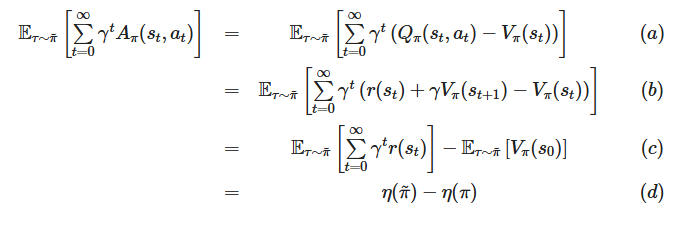 출처
출처
이제 위 1번식을 수정할건데 한가지 term을 정의해야한다.
아래는 P(st=s)를 가중해서 더한 값 즉 visitation frequency인데 normalized가 되어있지 않아 정확히는 (unnormalized) discounted visitation frequencies이다.
뜻은 π가 특정 state에 있을 확률들의 가중합을 의미한다.
ρπ(s)=P(s0=s)+γP(s1=s)+γ2P(s2=s)+...
이를 이용해서 (1)번식을 수정할 수 있는데
η(π~)=η(π)+Es0,a0,⋯∼π~[∑t=0∞γtAπ(st,at)](1)
이 식을 전개하면 아래와 같이 구성이 가능하다.
η(π~)=η(π)+∑t=0∞∑sP(st=s∣π~)∑aπ~(a∣s)γtAπ(s,a)=η(π)+∑s∑t=0∞γtP(st=s∣π~)∑aπ~(a∣s)Aπ(s,a)=η(π)+∑sρπ~(s)∑aπ~(a∣s)Aπ(s,a).(2)
첫번째 줄은 expectation을 제거한 것이고 두번째 줄은 sigma의 위치를 변경하고 γt가 t에대한 값이기 때문에 밖으로 뺀 것이다.
3번째 줄인 위 정의한 term을 이용해서 식을 간략하게 줄인 것이다.
여기에서 중요한 것은 π~로 π를 업데이트 할때 모든 state s에 대해서 advantage가 nonnegative면
즉,∑aπ~(a∣s)Aπ(s,a)≥0이면 항상 η(π~)가 증가하거나 유지되는 것을 보장한다.
이는 기존의 exact policy iteration에서 π~(s)=argmaxaAπ(s,a)로 업데이트할 때 advantage가 양수이고 state visit probability가 0이 아닌 상황이 1개라도 존재하면 policy가 개선이 됨을 보여준다.
하지만 실제로는 neural network로 근사해서 표현을 하기 때문에 exact policy가 될 수 없고 그렇기에 실제로는 ∑aπ~(a∣s)Aπ(s,a)<0인 상황인데 0보다 크거나 같다고 생각해서 update가 일어날 수 있다.
여기에서 중요한 것은 위 수식에서 ρπ~(s)가 사용이 되었기 때문에 π~의 trajectory를 구하고 state에 위치할 확률을 구해야 한다. 이는 update를 매우 어렵게 만든다. update를 하기 위해서 trajectory를 미리 구해봐야 하기 때문
그렇기에 위 수식의 ρπ~(s)를 ρπ(s) 수정해서 표현을 한다.
Lπ(π~)=η(π)+∑sρπ(s)∑aπ~(a∣s)Aπ(s,a).(3)
이렇게 수정하면 policy의 변경에 따른 visitation density의 변경을 무시하게 된다.
이렇게표현을 해도 괜찮을까?
당연히 괜찮지 않다.
그러나 policy를 조금만 변경하면 동일한 근사가 가능하다.
Lπθ0(πθ0)=η(πθ0),∇θLπθ0(πθ)∣∣∣θ=θ0=∇θη(πθ)∣∣∣θ=θ0.(4)
위 내용을 보면 Lπθ0(πθ0)인 상황은 당연하 advantage가 0이기 때문에 η(πθ0)와 동일하게 된다.
이때 양변을 미분한 것은 작은 step에 한해서 동일한 미분 값이 나오게 되고 그 미분 영역의 주변에서 근사 표현이 가능하다.
이 부분이 이해가 어려울 수 있는데
간단하게 2차 함수를 미분해서 표현하는 것을 생각하면 좋다.
 위 그림을 보면 2차함수를 미분해서 직선으로 구하였을 때 그 오차(빨간선)가 미분한 점에 가까울수록 줄어들게 된다. 이를 통해 작은 영역에서는 동일한 표현이 가능하고
위 그림을 보면 2차함수를 미분해서 직선으로 구하였을 때 그 오차(빨간선)가 미분한 점에 가까울수록 줄어들게 된다. 이를 통해 작은 영역에서는 동일한 표현이 가능하고
πθ0를 π~로 작은 step만큼 업데이트 하는 상황에서 Lπold를 증가시키면 η도 증가시킬 수 있다. 이를 통해서
'작은 step의 update가 이루어질 때' performance의 증가를 보장할 수 있다.
그런데 이 작은 step의 기준을 어떻게 정할 수 있을까?
kakade & langford의 논문에서 lower bound가 증명이 되었는데
πold가 현재의 policy이고 π′=argmaxπ′Lπold(π′)가 update될 policy인 상황에서
πnew(a∣s)=(1−α)πold(a∣s)+απ′(a∣s).(5)
위 상황 즉 π′과 πold의 비율을 통하여 mixture policy를 구성할 때
η(πnew)≥Lπold(πnew)−(1−γ)22ϵγα2,where ϵ=maxs∣∣∣Ea∼π′(a∣s)[Aπ(s,a)]∣∣∣.(6)
위와 같이 lower bound가 구성이 됨을 증명하였다.
위 수식에서 γ와 α는 고정된 constatnt 값이고 ϵ이 중요한데 ϵ은 advantage의 기댓값이 0이기 때문에 πold와 πnew의 차이가 작으면 0에 가까워지고 크면 커진다.
이를 이용해서 lower bound를 커지는 방향으로 update를 진행하면 η도 커지는 방향으로 update가 되기 때문에 monotonic imporvement를 보장할 수 있다.
하지만 이러한 lower bound는 policy가 섞이는 mixture policy에만 적용할 수 있기 때문에 실제 상황에서 적용하기에는 힘들다.
3 Monotonic Improvement Guarantee for General Stochastic Policies
이제부터 이 논문의 contribution이 시작된다.
우선 위 (6) 식을 practical하게 개선하는 것으로부터 시작한다.
우선 (5) mixture policy는 실제로 잘 사용되지 않기에 다른 방법으로 표현한다.
DTV(p∣∣q)=21∑i∣pi−qi∣라고 하자 즉 (31,0,0),(0,32,0)이면 21이다.
이를 이용해서 아래와 같이 DTVmax(π,π~)를 정의한다.
DTVmax(π,π~)=maxsDTV(π(⋅∣s)∥π~(⋅∣s)).(7)
Theorem1 α=DTVmax(π,π~)인 상황에서 lower bound는
η(πnew)≥Lπold(πnew)−(1−γ)24ϵγα2,where ϵ=maxs,a∣Aπ(s,a)∣.(8)
위처럼 정의가 된다.
여기에서 한번 더 정리가 들어가는데 pollard의 정리에 따르면
DTV(p∣∣q)2≤DKL(p∣∣q)를 만족시킨다.
그리고 위에서 DTVmax를 정의한 것처럼
DKLmax(π,π~)=maxsDKL(π(⋅∣s)∥π~(⋅∣s))라고 하자.
그러면 아래와 같이 정리가 가능하다.
η(π~)≥Lπ(π~)−CDKLmax(π,π~),where C=(1−γ)24ϵγ(9)
이제 이렇게 만든 식을 이용해서 이론적인 학습이 가능하다.
 위 알고리즘인데 간단하다.
위 알고리즘인데 간단하다.
위 수식을 이용해서 학습을 하는데
새로운 πi+1을 (9)식의 우변을 최대화 하는 π로 만든다.
이때 가능한 모든 advantage Aπi(s,a)를 전부다 구하는데 사실 이는 말이 안된다. state와 action이 무수히 많기 때문. 이론적으로 구성이 되기에 이렇게 작성이 되었다.
위 알고리즘 1 사용하면 monotonically improvement가 보장이 된다.
정확히는
η(π0)≤η(π1)≤η(π2)≤...이 됨을 보이기 위해서
Mi(π)=Lπi(π)−CDKLmax(πi,π)라고 할때
η(πi+1)≥Mi(πi+1) by Equation (9)η(πi)=Mi(πi), therefore,η(πi+1)−η(πi)≥Mi(πi+1)−M(πi).(10)
위와 같인 구조로 유도가 되고 만약 Mi가 각 iteration에서 non-decreasing을 만족하게 된다면 η도 non-decreasing을 만족한다.
이때 Mi를 surrogate function 즉 대리의 함수로 본다.(Mi를 증가하는 것이 곧 η의 증가이기 때문에 surrogate objective임)
4 Optimization of Parameterized Policies
지금까지는 parameter이 안된 π인 상황이었고 policy가 모든 state에서 평가가 될 수 있다고 가정을 하였다.
이제는 실질적인 parameterized policy 상황을 가져온다.
간단하게 이전 수식들을 parameterized 상황에서 어떻게 표현할지를 다룬다.
parameretized policy πθ(a∣s)와 parameter vector θ라고 하자.
이때 π대신 θ를 사용할 것이다.
예를 들어서 η(θ):=η(πθ), Lθ(θ~):=Lπθ(πθ~) 등등
이전에
maximizeθ[Lold(θ)−CDKLmax(θold,θ)].를 통해 η를 증가시킬 수 있음을 보였는데
이때 중요한 부분이 coefficient C=(1−γ)24ϵγ가 너무 크다는 것이다. 만약 γ=0.99면 분모가 0.012이 되고 분자에 10000이 곱해진다...
이 때문에 penalty가 너무 세서 step이 작아질 수밖에 없다.
그렇기 때문에 penalty term의 coefficient를 빼고 constraint에 넣어서 최적화 진행을 해준다.
사실 이 부분은 이론적인 최적에서 실질적으로 적용을 하기 위해서 타협을 한 것이다.
maximizeLold(θ)subject toDKLmax(θold,θ)≤δ.(11)
여기에서 다시한번 더 조절을 하는데
DKLmax(π,π~)=maxsDKL(π(⋅∣s)∥π~(⋅∣s))로 앞서 정의가 되었는데 이때의 문제점은 max s를 찾기 위해서 모든 state를 전부 다 알아야 한다.
이는 말이 안되기에 한번 더 타협을 해서 휴리스틱을 이용해서 다음과 같이 평균으로 변경한다. 평균으로 된다면 Montecarlo로 비편향추정량을 구할 수 있기 때문
DKLρ(θ1,θ2):=Es∼ρ[DKL(πθ1(⋅∣s)∥πθ2(⋅∣s))].
결국 이를 반영해서
maximizeLold(θ)subject toDKLρθold(θold,θ)≤δ.(12)
으로 최종적으로 변경한다.
실험에서 이렇게 구성한 (12)식은 (11)식과 실질적으로 비슷한 성능을 보였다고 한다.
5 Sample-Based Estimation of the Objective and Constraint
이 부분은 앞서 설명한 (12)식을 monte carlo로 어떻게 approximate가 되는지 설명하는 부분이다.
위 식을 풀면 다음과 같다.
maximizeθsubject tos∑ρθold(s)a∑πθ(a∣s)Aθold(s,a)DKLρθold(θold,θ)≤δ.(13)
우선 첫번째로 ∑sρθold(s)[...]의 내용을 expectatoin으로 변경한다.
1−γ1Es∼ρθold[...]와 같이 변경한다.
이렇게 만들기 위해서는 확률로 표현이 되어야하고 이를 위해서 정규화를 해주어야 한다.
원래 ρπ(s)=P(s0=s)+γP(s1=s)+γ2P(s2=s)+...의 구성이었다.
그렇기에 ∑sρπ(s)=∑s∑i=0∞γiP(st=s∣π)이다.
이를 순서를 바꾸면 ∑i=0∞γi∑sP(st=s∣π)로 표현할 수 있고
여기에서 각 시간 t에서 모든 state에 있을 확률의 합은 1이다.
∑sP(st=s∣π)=1
그렇기에 ∑i=0∞γi∑sP(st=s∣π)=∑i=0∞γi
∑i=0∞γi=1−γ1이기 때문에 ∑sρπ(s)=1−γ1이다. 이전의 ρπ(s)는 unnormalized 였기에 정규화가 되지 않았는데 이를 총합으로 나누면 즉 (1−γ)ρπ(s)의 형태로 [0,1]의 분포로 정규화를 시켜줄 수 있다.
이를 통해 확률과 같이 표현이 가능하고
1−γ1Es∼ρθold[...]로 결국 표현이 가능해진다.
이후 Aθold를 Qθold로 바꾼다. 이 부분은 원래 REINFORCE에서도 사용하는 방법이기에 사용하는 것 같다.
그리고 importance sampling을 통해서 sum을 기댓값으로 바꾸는데
∑aπθ(a∣sn)Aθold(sn,a)=Ea∼q[q(a∣sn)πθ(a∣sn)Aθold(sn,a)].이렇게 된다.
그냥 앞부분에 q(a∣sn)q(a∣sn)을 곱해서 expectation으로 변경한 것이다.
q는 sampling distribution이다.
이 내용을 종합하면
maximizeθsubject toEs∼ρθold,a∼q[q(a∣s)πθ(a∣s)Qθold(s,a)](14)Es∼ρθold[DKL(πθold(⋅∣s)∥πθ(⋅∣s))]≤δ.
이렇게 표현이 된다.
DKL의 평균화 부분은 원래 평균이었기에 쉽게 바로 표현이 가능하다.
이를 활용한 학습 방법이 2가지가 있다
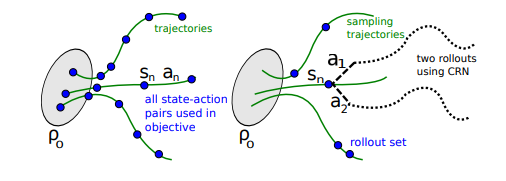
- single path: sampling individual rajectories에서 policy gradient로 학습
- vine: rollout set을 구성하고 각 rollout set의 state에서 multiple action을 진행
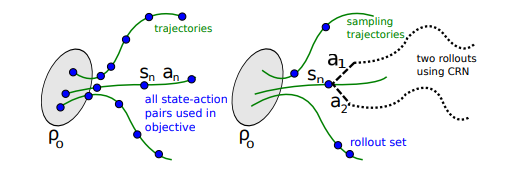 위 그림에서 왼쪽이 single path, 오른쪽이 vine이다.
위 그림에서 왼쪽이 single path, 오른쪽이 vine이다.
single path는 trajectory에서 state, action pair를 이용해서 학습
vine은 여러개의 trajectory를 만들고 도달한 state에서 branch rollout을 진행해서 여러경로를 동시에 학습 진행
5.1 Single Path
매우 간단하다.
s0∼ρ0에서 policy πθold를 따라서 trajectory s0,a0,s1,a1,...,sT−1,aT−1,sT를 생성하고 q(a∣s)=πθold(a∣s)의 상황에서
Qθold(s,a)를 계산하고 (14)의 최적화 문제를 푸는 방향으로 학습을 진행
5.2 Vine
이 부분이 조금 어려운데
s0∼ρ0에서 policy πθi를 따라서 trajecyory를 여러개 생성하는데 이때 subset N개만큼의 state를 고른다. s1,s2,...,sN 이를 rollout set이라고 부른다.
각 state에서 action K개를 sampling하는데 an,k∼q(⋅∣sn)으로 생성한다.
이때 q(⋅∣sn)=πθi(⋅∣sn)는 continuous problem에서 잘 작동했고 uniform distribution은 exploration에 도움을 줘서 아타리 등의 discrete task에서 잘 작동했다고 한다.
sampling한 state와 action을 시작으로 rollout을 진행해서
Q^θi(sn,an,k)를 추정한다. 이를 동일한 난수 시퀀스로 여러번 뽑음으로써 rollout의 variance를 줄일 수 있다.
이때 작고 유한한 공간에서는 state에서 모든 action에 대한 rollout을 만들 수 있다. 특정한 상태 sn에서 기여하는 부분은 다음과 같다.
Ln(θ)=∑k=1Kπθ(ak∣sn)Q^(sn,ak),
이는 state sn에서의 L 추정치인데 이를 모든 rollout state에서 평균내서 바꿔서 기존의 목표함수 Lθold로 바꿔줘야한다.
이를 importance sampling을 이용해서 self-normalized estimator로 만들 수 있는데
single state sn에서 얻어지는 Lθold는 다음과 같다.
Ln(θ)=∑k=1Kπθold(an,k∣sn)πθ(an,k∣sn)∑k=1Kπθold(an,k∣sn)πθ(an,k∣sn)Q^(sn,an,k),
이렇게 분모로 나눠주는 이유는 importance의 비율이 있으면 분산이 높을 수 있기에 이를 나눠서 정규화를 해주기 위함이다.

single에 비해서 vine의 장점은 여러번 계산하기 때문에 분산이 낮다는 것이다.
그러나 계산량이 너무 늘어나고 rollout을 위해서는 이전의 상태로 언제든지 돌아갈 수 있어야 한다.
8 Experiments
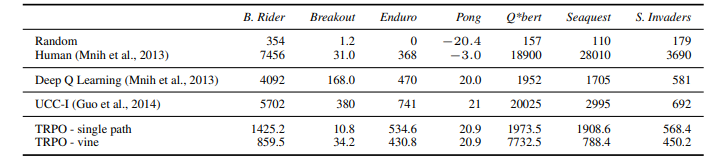 의외로 성능은 뛰어나지 않고 DQN과 비슷하다.
의외로 성능은 뛰어나지 않고 DQN과 비슷하다.
성능보다는 이렇게 학습이 된다는 다룬 논문이라서 그렇다고 한다.
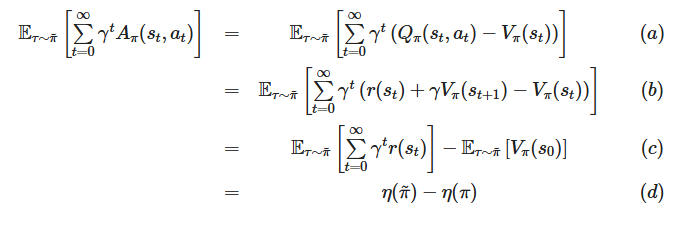 출처
출처위 그림을 보면 2차함수를 미분해서 직선으로 구하였을 때 그 오차(빨간선)가 미분한 점에 가까울수록 줄어들게 된다. 이를 통해 작은 영역에서는 동일한 표현이 가능하고
위 알고리즘인데 간단하다.
 위 그림에서 왼쪽이 single path, 오른쪽이 vine이다.
위 그림에서 왼쪽이 single path, 오른쪽이 vine이다.
 의외로 성능은 뛰어나지 않고 DQN과 비슷하다.
의외로 성능은 뛰어나지 않고 DQN과 비슷하다.