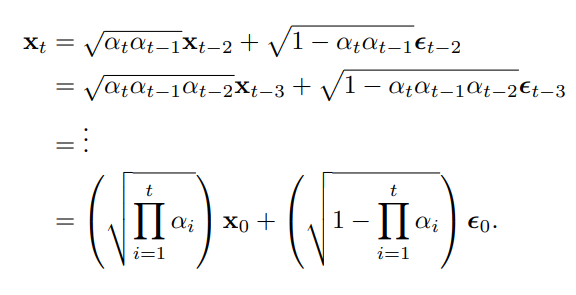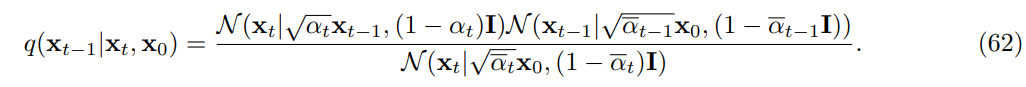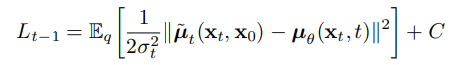
유명한 diffusion 논문이다.
1 Introduction
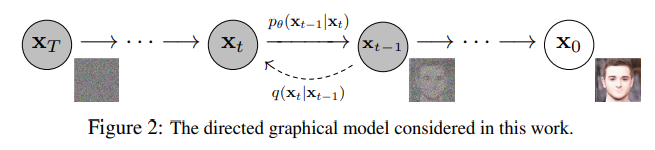 diffusion은 markov chain(이전 step이 현재의 step에 영향을 주지 않음.)을 통해서 학습이 된다.
diffusion은 markov chain(이전 step이 현재의 step에 영향을 주지 않음.)을 통해서 학습이 된다.
noise를 더해서 gaussian noise로 만든 다음 복구하는 구조.
재밌는건 diffusion이 왜 high quality sample을 만드는지 증명이되지 않았지만 이 논문에서는 실제로 잘 작동한다는 것을 보여준다.
2 Background
수식이 굉장히 많다...
이전글에 작성하였는데
Tutorial on Diffusion Models for Imaging and Vision
이 논문을 보고오면 이해가 빠르다!
위 논문의 내용을 위주로 덧붙여서 설명을 진행하겠다.
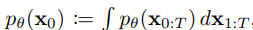 우선 처음 시작은 위와 같다. 위는 marginal distribuion으로 를 모두 더해주기에 왼쪽과 동일해진다.
우선 처음 시작은 위와 같다. 위는 marginal distribuion으로 를 모두 더해주기에 왼쪽과 동일해진다.
-
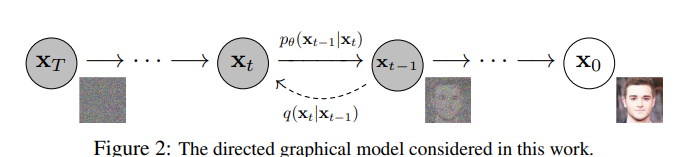
이후 각 reverse 분포는 아래 수식과 같은데
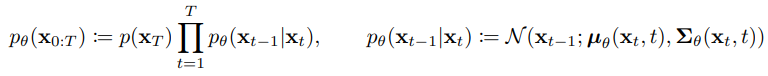 이전 timestep을 복구하는 구조이다. 오른쪽은 VAE와 비슷하게 mean, variance를 modeling하는 것을 의미한다.
이전 timestep을 복구하는 구조이다. 오른쪽은 VAE와 비슷하게 mean, variance를 modeling하는 것을 의미한다. -
이후 forward분포는 아래와 같다.
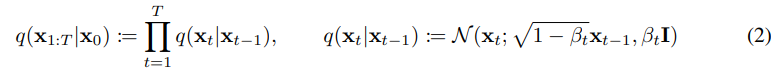 위 내용은 reverse와 사실상 동일한데 neural network가 아니라 단순히 각 고정된 값을 곱해줘서 점점 gaussian noise에 가깝게 만들어지는 구조이다.
위 내용은 reverse와 사실상 동일한데 neural network가 아니라 단순히 각 고정된 값을 곱해줘서 점점 gaussian noise에 가깝게 만들어지는 구조이다.
이다. -
이후 위 수식을 바탕으로 아래와 같이 만들어준다.
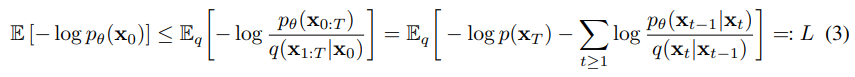 하나씩설명하자면 왼쪽은 neural network의 log-likelihood이다. 즉 를 생성할 확률 오른쪽은 왼쪽에서 유도된 값인데
하나씩설명하자면 왼쪽은 neural network의 log-likelihood이다. 즉 를 생성할 확률 오른쪽은 왼쪽에서 유도된 값인데
 유도 과정은 위와 같다. 베이즈 정리를 이용해서 진행을 한다. 위 유도에서는 기댓값이 encoder network의 분포로 되었는데 원본 수식에서는 encoder network가 아니기에 원본 encoder 분포 로 사용하였다.
유도 과정은 위와 같다. 베이즈 정리를 이용해서 진행을 한다. 위 유도에서는 기댓값이 encoder network의 분포로 되었는데 원본 수식에서는 encoder network가 아니기에 원본 encoder 분포 로 사용하였다.
이제 추가로로 누적곱이다.
이를 이용해서 encoder의 t step을 바로 도출할 수 있다.
유도는
위 수식에서
w는 mean=0, var은 각각의 제곱이기에아래와 같다.
이를 계속 이어가면
이렇게 된다.
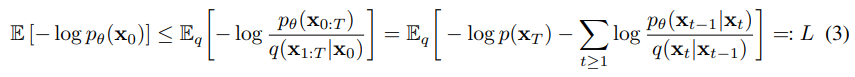 이후 위 수식을 계속 정리해서 ELBO를 만들면
이후 위 수식을 계속 정리해서 ELBO를 만들면
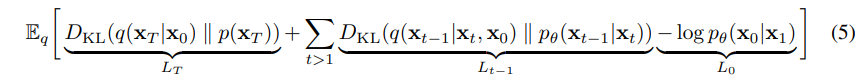 위와 같이 전개가 되는데
위와 같이 전개가 되는데
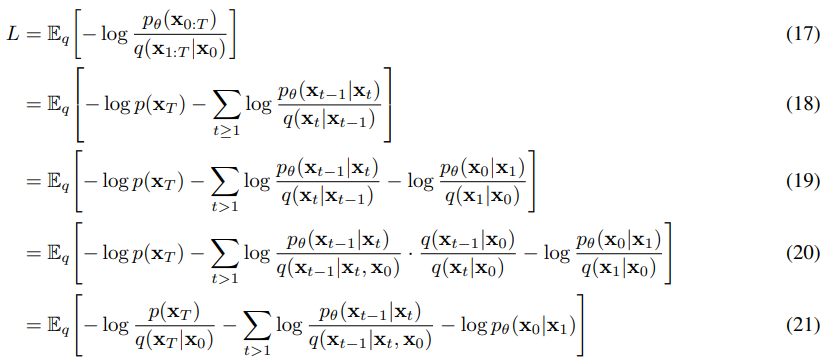
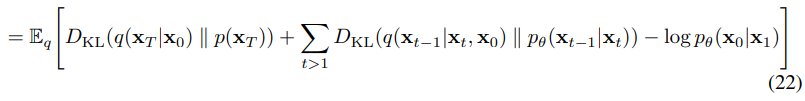
위처럼 진행이 된다.
이부분의 유도과정은 대부분 쉬운데
forward 을 로 바꾼 방법은 간단하게 베이즈 정리이다.
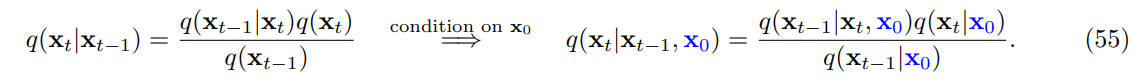
이때 위 수식에서
이 부분이 나오는데
이 부분의 유도는 조금 어렵다.
위 를 베이즈 정리를 통해서 로 표현할 수 있고 그게 아래의 수식이다.
이후 이들은 가우시안 곱으로 표현가능하기에 각 분포를 수식으로 만든 것을 곱하면
아래와 같이 exp의 지수가 나오고 이 지수의 미분하였을 때 0을 만드는 값이 원본에서는 평균, 그리고 이계도함수의 역이 분산이기에 이렇게 구하면 위와 같은 평균, 분산의 값이 나온다.
3 Diffusion models and denoising autoencoders
를 param으로 학습이 될수도 있지만 고정된 값도 된다. 그렇기에 이를 배제하고 진행.
3.1 Forward process and
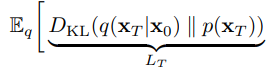 앞의 loss의 이 부분인데 q는 학습가능하지 않기에 무시
앞의 loss의 이 부분인데 q는 학습가능하지 않기에 무시
3.2 Reverse process and
앞의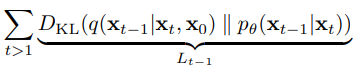 이부분.
이부분.
로 어떻게 진행할지 선택지를 생각.
우선 로 임의의 상수 선택한다고 한다.
경험적으로와 는 비슷한 결과를 보였다고 한다.
두 경우에서 첫번째는 에서 optimal이고 두번째는 가 1개의 점으로 deterministic하면 optimal이라고 한다.
위 KL divergence를 전개해서
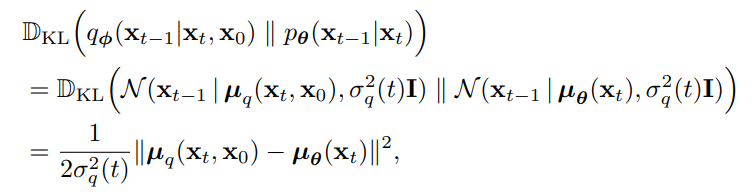 위와 같이 loss를 진행할 수 있다. (variance가 동일하면 사실상 평균의 제곱)
위와 같이 loss를 진행할 수 있다. (variance가 동일하면 사실상 평균의 제곱)
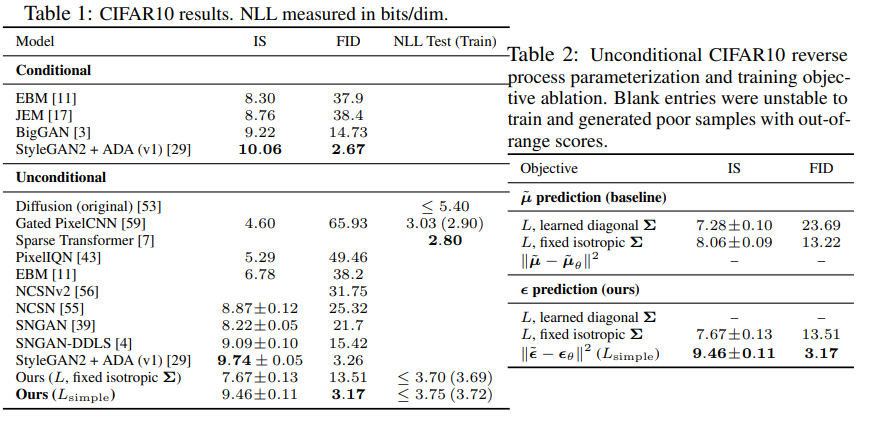
실제 논문의 값은 아래와 같다.
이후 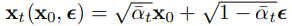
위 수식을 대입해서
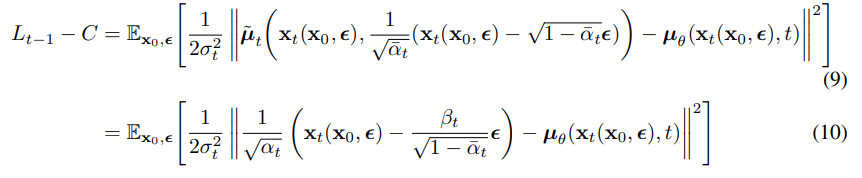
위와 같이 전개한다.
(9)는 단순하게 대입을 한 것이고 (10)은
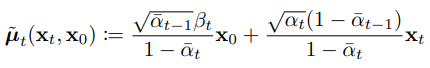 이를 넣어서 정리한 것이다. (background에서 유도하였음.)
이를 넣어서 정리한 것이다. (background에서 유도하였음.)
이는 가 을 예측해야 하는 것을 의미한다.
이떄 는 neural net의 output이기에 우리가 임의로 목적을 바꿔도 된다.
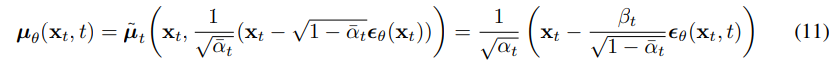 목적을 위와 같이 바꾸면 오른쪽 부분은 위의 목적과 epsilon 부분을 제외하고 똑같아진다.
목적을 위와 같이 바꾸면 오른쪽 부분은 위의 목적과 epsilon 부분을 제외하고 똑같아진다.
이제 에서 noise를 예측하는 것과 동일해졌다.
결국 위 값이 평균이기에 inference에서는
를 sampling하기 위해서는
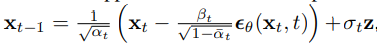 위와 같이 sampling이 되어야 한다.
위와 같이 sampling이 되어야 한다.
마지막으로 loss에 바꾼 를 넣으면
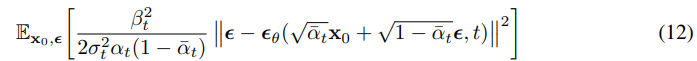 위 처럼 loss가 만들어진다.
위 처럼 loss가 만들어진다.
사실 노이즈 대신 를 예측하도록 할 수있는데 이러면 task가 너무 복잡해져서 학습이 잘 되지 않는다.
3.3 Data scaling, reverse process decoder, and
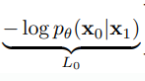 마지막 부분이다.
마지막 부분이다.
이미지 데이터가 로 구성된 것을 로 linear scaling을 진행하였다고 하자.
그럼 아래 그림과 같이 이산화를 시킬 수 있다.
아래 그림에서 는 data의 dim이다.
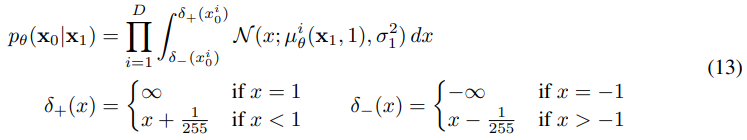 사실 처음 봤을 때 수식이 와닿지 않았는데
사실 처음 봤을 때 수식이 와닿지 않았는데
의미는 간단하다. Normal 분포로 X가 추출되기 때문에 이 값은 무슨 값이든지 가능하다.
이를 원본 값으로 mapping을 해주는 것으로
아래 수식은 만약 원본 x가 1이면 무한대까지 범위를 설정하고 -1이면 -무한대 까지 범위를 설정하는 것이다.
그게 아니라면 원본 x에 따라서 각 범위를 원본 ~ 의 범위의 확률을 구해서 얼마나 원본을 잘 복구하는지 구하는 것이다.
즉 random 분포를 이산화 하는 것이다.
3.4 Simplified training objective
위 수식들을 바탕으로 일반화된 목적은 다음과 같다.
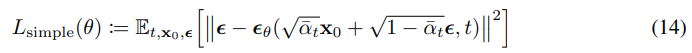 참고로 이렇게 simple하게 만든 loss가 더욱 좋은 성능이 나왔다고 한다.
참고로 이렇게 simple하게 만든 loss가 더욱 좋은 성능이 나왔다고 한다.
위 수식에서 는 1~까지 uniform 샘플링 되는데 t=1이면 바로 위의 이고 그게 아니면 transition loss이다.
transition loss는 앞부분의 곱해지는 부분을 제외하면 위 수식과 동일하지만 가 어떻게 저기에 통합될 수 있을까?
논문의 설명은 다음과 같다.
The t = 1 case corresponds to with the integral in the discrete decoder definition (13) approximated by the Gaussian probability density function times the bin width, ignoring and edge effects.
대강 의미는 bin의 넓이를 곱하고 을 무시하고 가우시안 확률 밀도 함수로 근사했다고 한다.
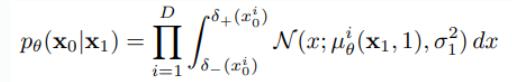 원본의 수식이 위와 같을때
원본의 수식이 위와 같을때
이 내부의 수식을 을 무시한다는 것은 디렉 델타 함수 즉 1개의 점에서만 확률을 가지게 되고 가 에서한 확률을 가지게 된다는 것을 의미한다. 이후 적분과 비슷하게 를 곱하게 된다.
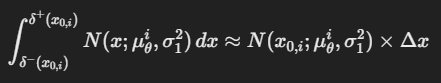 이렇게 되고(는 )
이렇게 되고(는 )
원본 loss처럼 -log를 붙이면
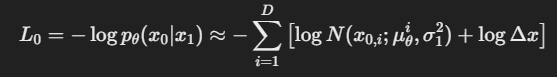 이렇게 표현이 가능하고 델타 x는 최적화 과정에서 에 독립적이라 무시가 가능하다.
이렇게 표현이 가능하고 델타 x는 최적화 과정에서 에 독립적이라 무시가 가능하다.
이를 다시 가우시안 밀도 함수로 바꾸면
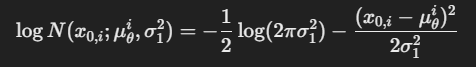 위와 같고
위와 같고
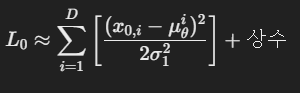 loss는 이제 이렇게 표현이 되고
loss는 이제 이렇게 표현이 되고
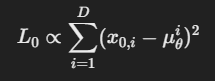 이렇게 된다.
이렇게 된다.
이후 noise를 예측하도록 바꾸는 부분은 위에 과 비슷하니 끝.
추가로 위에 간단화된 loss는 앞의 weighted term을 버리게 되는데 이는 loss가 집중되는 비율이 바뀜을 의미한다.
이를 좀 반영해주기 위해서 실제 실험에서는 t가 작을 때 loss의 중요도를 조금 내려주었다고 한다.
noise가 매우 적은 데이터를 복구하기 때문에 중요도를 추고 noise가 많은 데이터를 학습하는 것이 도움이 된다고 한다.
실제로 이렇게 중요도를 수정하는 것이 성능을 향상시켜준다고 한다.
4 Experiments
실제 실험에서는 이고 에서 까지 linearly하게 구성했다고 한다.
이는 data의 scale [-1,1]을 토대로 상대적으로 작은 값을 만들었다고 한다.
이러면
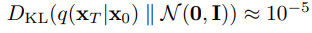 으로 noise와의 차이가 실제 실험에서 매우 작게 나온다고 한다.
으로 noise와의 차이가 실제 실험에서 매우 작게 나온다고 한다.
reverse process는 U-net으로 backbone을 설정.
param은 각 time에 대해서 share한다.
그리고 time step은 transformer의 positional embedding을 표현할때 사용한 sin파를 통해 model에게 알려준다.
그리고 U-net에서 feature map이 16x16이면 self-attention을 진행했다고 한다.
구현
링크에 구현을 하고 설명을 작성해두었다.