[ML] Grdient Descent (경사하강법)

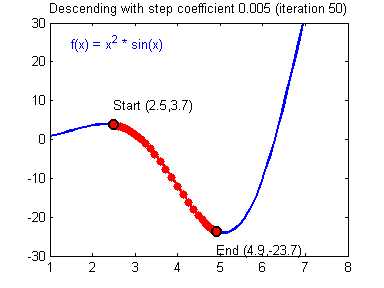
1. Gradient Descent (경사하강법)

• 딥러닝 알고리즘을 학습할 때 사용되는 최적화 방법(optimizer)중 하나

• Loss Function의 크기를 최소화시키는 파라미터를 찾는 것

• Loss Function의 변화에 따라 가중치(w)와 편향(b)를 업데이트해야 할 때, 최적의 가중치를 찾는 방법으로 사용됨

• 함수의 기울기(grdient)를 이용하여 $x$의 값을 특정한 위치로 옮겼을 때 함수가 최솟값을 갖는지 알아보는 방법

• 기울기의 반대 방향으로 내려가는 식으로 진행됨

  1. 기울기가 양수이면, $x$의 값이 커질수록 함수값이 커짐 → 음의 방향으로 $x$를 옮겨야함
  2. 기울기가 음수이면, $x$의 값이 커질수록 함수값이 작아짐 → 양의 방향으로 $x$를 옮겨야함

• 수식

  $x_{i+1} = x_{i} - \alpha\nabla f (x_i)$

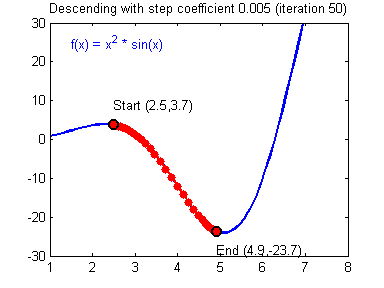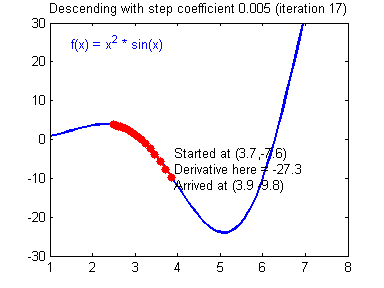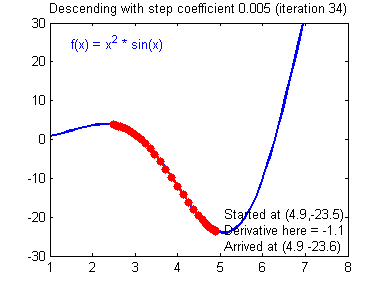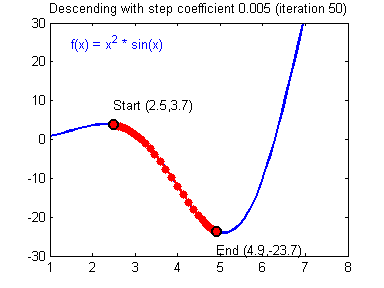
2. Learning Rate (학습률)

• Step Size라고도 부름

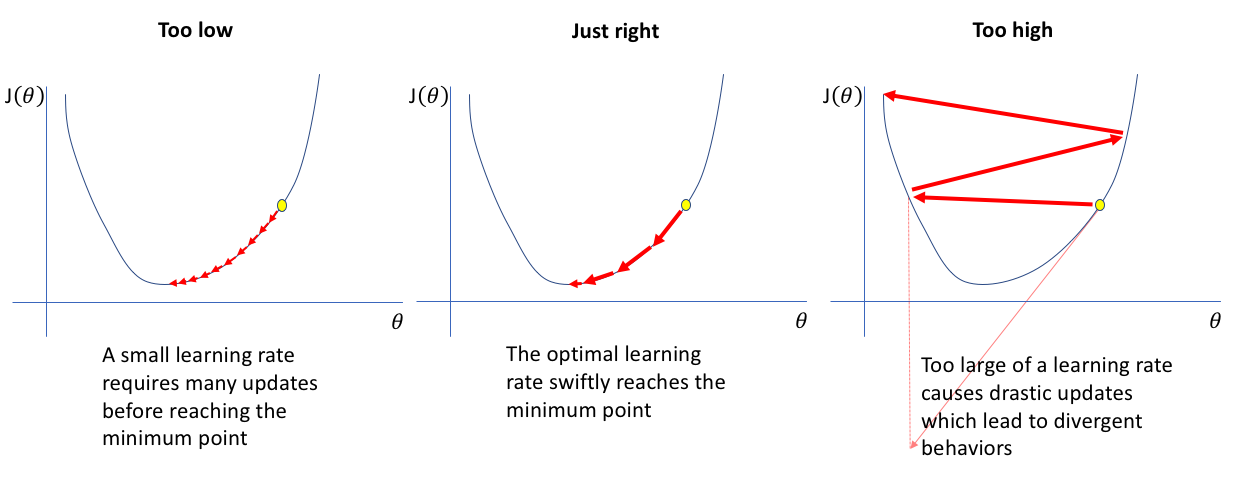
• Learning Rate가 큰 경우 한 번 이동하는 거리가 커지므로 빠르게 수렴할 수 있다는 장점이 있지만, 최소값을 계산하도록 수렴하지 못하고 함수 값이 계속 커지는 방향으로 최적화가 진행될 수 있다(발산).

• Learning Rate가 작은 경우 발산하지 않을 수는 있지만 $x$를 구하는데 소요되는 시간이 오래 걸림

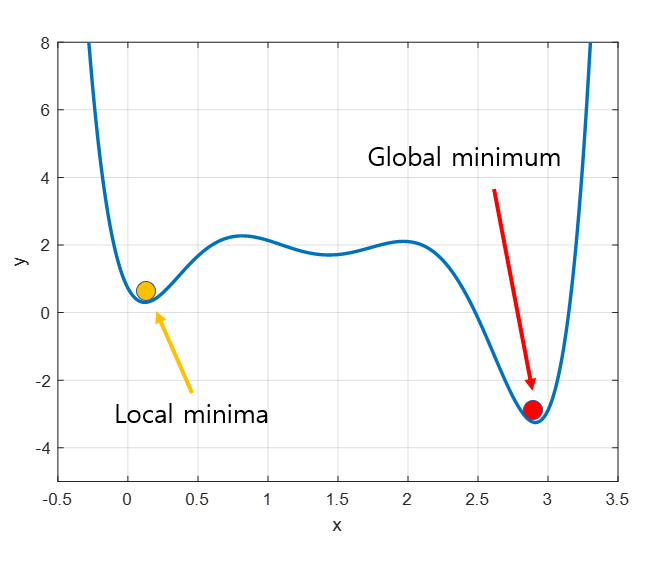
3. Local Minima 문제

• 실제 목표는 global minima를 찾는 것이지만 시작하는 위치가 랜덤하므로 어떤 경우에는 local minima에 빠져 계속 헤어나오지 못할 수도 있는 문제가 발생 → 다양한 optimization 기법을 이용
  

4. Gradient Descent 종류

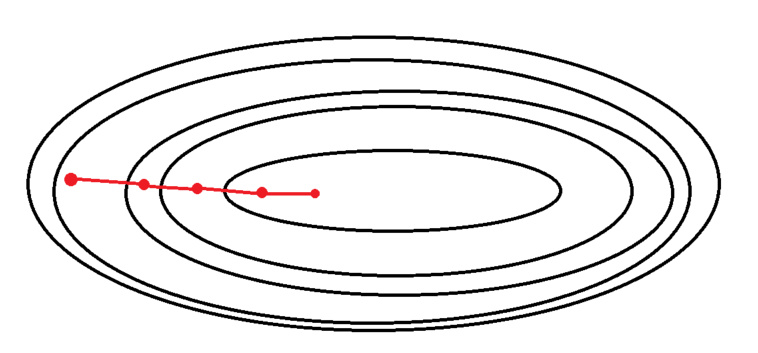
1. Batch Gradient Descent (배치 경사 하강법)

• 가장 기본적인 경사 하강법

• loss function의 기울기 계산에 전체 학습 데이터셋에 대한 에러를 구한 뒤 기울기를 한 번만 계산

• 한 번의 Epoch에 모든 parameter 업데이트를 한 번만 수행 (1 epoch 당 1회 parameter update)

• Global minima 에 대한 수렴이 안정적으로 진행 BUT local minima 상태가 되면 빠져 나오기 힘듦

• Parameter를 업데이트 할 때, 한 번에 전체 데이터셋을 고려하기 때문에 모델 학습 시 많은 시간과 메모리가 필요

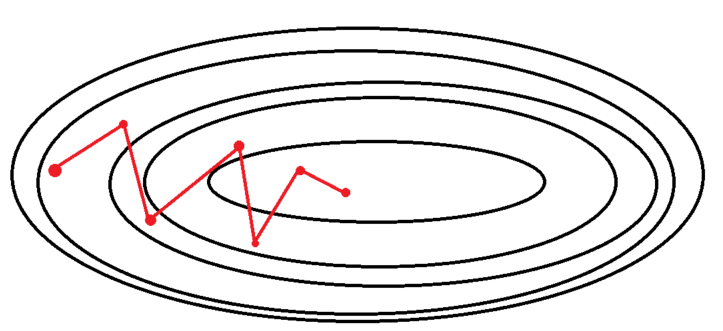
2. Stochastic Gradient Descent (확률적 경사 하강법)

• 학습 데이터셋에서 무작위로 한 개의 샘플 데이터셋을 추출해 그 샘플에 대해서만 기울기를 계산하는 방법 = 추출된 데이터 한 개에 대해서 에러를 계산하고 Gradient Descent 알고리즘을 적용하는 방법

• 샘플 데이터셋에 대해서 기울기를 계산하므로 반복할 때마다 다뤄야 할 데이터가 줄어듦 + 학습 속도가 빠르고 메모리 소모량이 낮으며, 큰 데이터 셋도 학습이 가능

• 학습 중간 과정에서 진폭이 크고 배치 경사 하강법보다 불안정하게 움직임 → global minima에 정확히 도달하지 못할 가능성이 있음 BUT Local minima에 빠지더라도 쉽게 빠져나올 수 있음

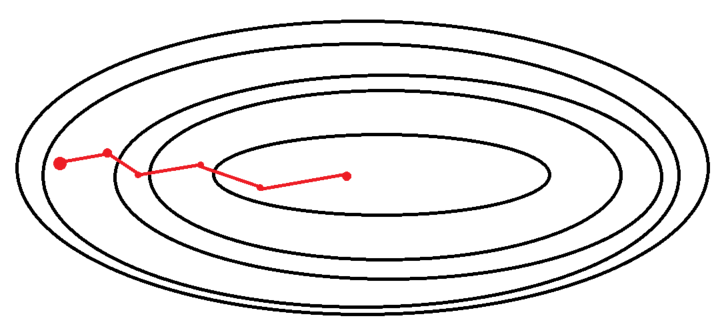
3. Minibatch Gradient Descent (미니배치 경사 하강법)

• SGD와 BGD의 절충안

• 최근에 많이 사용하는 방법

• 배치 크기를 줄여 SGD를 이용하는 방법

• 전체 데이터를 Batch size만큼 나누어 SGD를 진행
  Ex. 전체 데이터 셋이 100개 batch size가 10이면 총 10개의 mini batch생성 → 1 epoch당 SGD 10번 진행

• 전체 데이터 셋을 대상으로 하는 SGD보다 parameter공간에서 shooting이 줄어듦

• SGD에 비해 local minima에 빠질 위험이 줄어듦

Reference

https://angeloyeo.github.io/2020/08/16/gradient_descent.html
https://velog.io/@crosstar1228/MLGradient-Descent-%EC%9D%98-%EC%84%B8-%EC%A2%85%EB%A5%98Batch-Stochastic-Mini-Batch
https://velog.io/@cha-suyeon/%ED%98%BC%EA%B3%B5%EB%A8%B8-%EB%B0%B0%EC%B9%98%EC%99%80-%EB%AF%B8%EB%8B%88-%EB%B0%B0%EC%B9%98-%ED%99%95%EB%A5%A0%EC%A0%81-%EA%B2%BD%EC%82%AC%ED%95%98%EA%B0%95%EB%B2%95